
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача о наименьшем числе аварий.
Пусть множество Х – множество печей для обжига кирпича, а множество У – множество платформ для сушки кирпича. Печи соединены с платформами рельсами. В месте пересечения рельсов вагонетки могут сойти с рельса. Ясно, чем меньше пересечений, тем меньше аварий. Каково наименьшее число аварий? Поставим задачу в математическом виде. Пусть имеется двудольный граф G Введем обозначения: J(m, n) – функция, значением которой является число таких точек пересечения. Нам известно, что граф Понтрягина – Куратоввского имеет не менее одного пересечения, т.е. J(3, 3) Справедлива Теорема
. Доказательство: На первом этапе докажем, что эта теорема справедлива при m =3: m=3, значит r=1, и тогда должно быть .
Воспользуемся методом математической индукции:
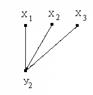
Рис. 21. Двудольный граф (3,2.
Предположим, что теорема справедлива для некоторого s и докажем, что она справедлива для s+1. Мы должны будем получить:
Разобьем граф G
х1 х2 х33
● ● yi yj
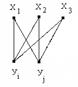
Рис. 22. Разбиение графа на подграфы и пример объединения их в пары.
Будем рассматривать всевозможные пары этих подграфов G Может оказаться, что каждая пара имеет хотя бы одну точку пересечения. Общее число пар
Полагая, что S=S+1, получим n=2(S+1), если n - четное (2), n=2(S+1) +1, если n – нечетное. (3) Подставим формулу (2) в (1): Получим:
Теперь подставим (3) в (1):
Предположим теперь, что имеется пара G Мы доказали, что при m=3 исходная формула справедлива. Докажем теперь, что формула для оценки общих точек пересечения справедлива для любого m:
Воспользуемся методом индукции, т. докажем справедливость формулы (5) для
Рассмотрим первый случай. При r=s=1 формула справедлива.
Рис. 23. Разбиение графа на подграфы.
Объединим последовательно 1 – ый и 2 – ой, 3 – ий и 4 – ый…: (1,2), (3,4),…, (2r-1,2 r) подграфы. По индуктивному предположению формула (5) справедлива. Добавим х
Получим:
или
Пусть теперь m=2r+1 (нечетное). Тогда при разбиении на пары подграфов последней вершине m – ой не хватает пары. Но если мы добавим (m+1) – ую вершину, то получим подграф G Если добавляется вершина во множество у, доказательство ничем отличаться не будет. Если же вершина добавляется во множества х и у, то сначала доказывается добавление во множество х, а потом во множество у.
Что и требовалось доказать. Пример: m=4, n=4, тогда r=2, s=2. J (4, 4)
Взвешенный граф. Пусть задан граф G(V,E). Если каждому ребру этого графа поставлено в соответствие некоторое число, то граф называется взвешенным. При задании взвешенных графов в матрицу смежности (или список) заносятся веса. Задача о кратчайшем пути. Пусть задан связный взвешенный граф. Будем истолковывать его вершины как населенные пункты, а веса как расстояния между ними. Поставим задачу о нахождении такого маршрута, соединяющего х
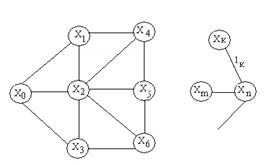
Рис. 24. Пример дорожного графа.
Обозначим l Алгоритм Форда.
Сущность этого алгоритма заключается в том, что каждой i – той вершине ставится в соответствие некоторое число
Обозначим через l Пусть назначена то полагаем И так до тех пор, пока не дойдем до
Обратный ход: Мы получили Среди расстояний, соединяющих х Затем ищем вершину х Замечание 1: При каждом поиске предыдущей вершины обратного хода необходимо проверять все смежные вершины, так как предыдущая вершина может быть не единственной. Замечание 2: Изменение значения Обоснование алгоритма: Так как значение
Рис. 25. Пример взвешенного графа.
1) i=0, j=1,2,3; j=1: j=2: j=3: 2) i=1, j=0,2,4 (0 –уже не рассматриваем) j=2: j=4: 3) i=2, j=0, 1, 3, 4. j=0; не рассматриваем j=1:
j=3: j=4: 4) i=3, j=0,2,5,6; j=0; не рассматриваем j=2: j=5: j=6: 5) i=4, j=1,2,5,7; j=1: j=2: j=5: j=7: 6) i=5, j=3,4,6,7; j=3: j=4: j=6: j=7: 7) i=6, j=3,5,7; j=3: j=5: j=7: 8) i=7, j=4,5,6; j=4; не рассматриваем j=5; не рассматриваем j=6:
Получили схему:
Обратный ход: Начиная с последней вершины, проверяем все ей смежные на выполнение условия: l Получим кратчайший путь хПоучаем: х
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2022-09-03; просмотров: 40; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.161.92 (0.083 с.) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 , где m и n – мощности множеств Х и У соответственно. Предположим, что вершины и ребра расположены в одной плоскости. В каждой точке, отличной от вершины пересекаются не более двух ребер. Оценим общее количество внутренних точек пересечения двудольного графа.
, где m и n – мощности множеств Х и У соответственно. Предположим, что вершины и ребра расположены в одной плоскости. В каждой точке, отличной от вершины пересекаются не более двух ребер. Оценим общее количество внутренних точек пересечения двудольного графа.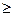 1.
1.
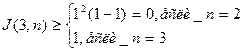 ,что справедливо. Граф (3,2) не имеет пересечений, в чем достаточно просто убедиться (рис. 21), а граф (3,3) - это граф Понтрягина – Куратоввского, имеющий одну точку пересечения.
,что справедливо. Граф (3,2) не имеет пересечений, в чем достаточно просто убедиться (рис. 21), а граф (3,3) - это граф Понтрягина – Куратоввского, имеющий одну точку пересечения.
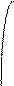


 ● ●
● ●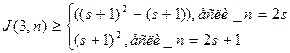 =
= 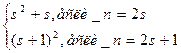 . (*)
. (*)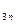 на подграфы.
на подграфы. 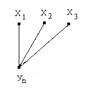

 :
: 


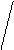

 (i
(i 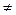 j):
j):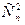
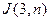 =
=  (1),
(1), , что совпадает с оценкой (*).
, что совпадает с оценкой (*).
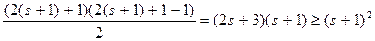 , что совпадает с оценкой (*).
, что совпадает с оценкой (*).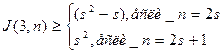 . Добавим вершину n+1:
. Добавим вершину n+1: 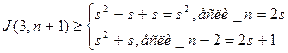 , что совпадает с оценкой (*).
, что совпадает с оценкой (*).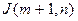 ,
, 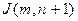 ,
,  .
.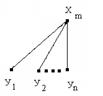
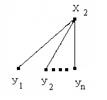
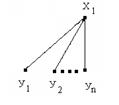 Предположим, что m=2r. Разобьем граф G
Предположим, что m=2r. Разобьем граф G  на подграфы и пронумеруем их:
на подграфы и пронумеруем их: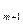 вершину. Эта вершина с каждой парой подграфов образует подграф G
вершину. Эта вершина с каждой парой подграфов образует подграф G  -s), если n=2s, и s
-s), если n=2s, и s 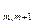 . Может оказаться, что этот подграф имеет точки пересечения или не имеет их. Если не имеет, то наша оценка не изменится, а если имеет, то только усилится.
. Может оказаться, что этот подграф имеет точки пересечения или не имеет их. Если не имеет, то наша оценка не изменится, а если имеет, то только усилится.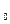 и х
и х 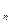 , что сумма расстояний была минимальной (маршрут не обязан включать все вершины).
, что сумма расстояний была минимальной (маршрут не обязан включать все вершины).
 , значение которого зависит от значения
, значение которого зависит от значения 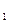
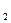
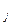 -
- 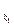 +l
+l 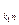 (1*)
(1*) 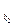 , у которой
, у которой  Пример:
Пример: -
- 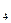 >
> 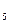 =4+6=10; заносим в таблицу.
=4+6=10; заносим в таблицу. =
= 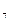 =
= 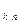 =
= 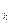 .
. 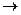 х
х 


