
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгоритмически неразрешимые проблемы. ⇐ ПредыдущаяСтр 10 из 10
Некоторые из них нам уже известны: 1. Проблема распознавания характера формулы в ЛП (ИП). 2. Алгоритмическая разрешимость проблемы нахождения корней уравнения степени выше 4. 3. К этим же проблемам относится проблема распознания самоприменимости машины Тьюринга; проблема ставится так: на ленте машины Тьюринга в терминах внешнего алфавита записана программа данной машины. Применима ли машина к полученной конфигурации? Алгоритма распознавания нет. 4. Проблема существования целых корней так называемого диафантого уравнения F(x, y, …, t)=0, где F – многочлен с целыми коэффициентами. Однако неразрешимость алгоритмически тех или иных проблем не означает, что отдельная задача или даже классы задач не могут найти решения.
Интуитивное понятие сложности алгоритма.
1) Сложность есть некая объективная количественная характеристика алгоритм, которая может зависеть от решаемых задач. Формально, если А-алгоритм, Р-класс решаемых задач и рєР, то сложность есть число α=α(А,р), сопоставляемое паре А и р. Например, в качестве числовой характеристики алгоритма может быть затрата времени, которая вычисляется, как τn, где n – число шагов, выполняемых при решении задач, τ – среднее время, затрачиваемое на 1 шаг. Здесь n – такая объективная характеристика.
2) Мерой сложности алгоритма назовем характер той числовой функции, которая зависит от числа шагов n, выполняемых при решении задач данного класса. В свою очередь n может меняться от задачи к задаче будучи зависимой от «размера» исходных данных. Например, говорят, что алгоритм имеет полиноминальную сложность, если мера сложности есть Ps(n), где P-многочлен S-ой сложности. Другие меры сложности: а) Логарифмическая; б) Экспоненциальная. Пример. Алгоритм поиска элемента с заданными свойствами среди данных n-элементов (например, страница с опечаткой в пачке листов бумаги).
3) С точки зрения математики сравнение алгоритмов (т.е. мер их сложности) разумно проводить при больших n. Т.е. для двух данных мер сложности f(n), g(n) производится сравнение δδ, т.е рассматривается lim(f(n)/g(n)). Например, алгоритм g будет сложнее f, если lim=0; алгоритмы будут одного порядка сложности, если lim=const≠0.
Основные понятия нечёткой логики.
Нечёткие множества. Определение 1. Пусть задано некоторое непустое множество Х. Нечетким называется множество A, определенное как множество пар вида: Множество Х называется базовым множеством, а функция Замечание 1. Значения функции принадлежности формируются субъективно и могут иметь различный вид для одного и того же субъекта при различных обстоятельствах и настроениях. Определение 2. Высказывание A называется нечетким, если допускается, что оно может быть одновременно истинным и ложным (что определяется различными обстоятельствами и настроениями). Любое оценочное суждение, основанное на неполных или недостоверных данных, является нечетким и сопровождается обычно выражением степени уверенности (или сомнения) в его истинности. Например, утверждение: "Скорее всего, завтра похолодает". Определение 3. Мера (степень) истинности нечеткого высказывания A определяется функцией принадлежности Замечание 2. Четкое истинное высказывание характеризуется функцией принадлежности
Нечеткие высказывания могут быть простыми и составными. Составные высказывания образуются из простых с помощью логических операций, называемых также логическими связками. 1) Результатом отрицания нечеткого высказывания A называется нечеткое высказывание Ā (A), степень истинности которого определяется выражением: 2) результатом конъюнкции нечетких высказываний A и B называется нечеткое высказывание АÙВ, степень истинности которого определяется выражением: 3) дизъюнкция нечетких высказываний A и B приводит к нечеткому высказыванию AÚB, степень истинности которого определяется выражением: 4) степень истинности «нечеткой импликации» А→В нечетких высказываний A и B определяется выражение:
5) эквиваленция нечетких высказываний A и B приводит к нечеткому высказывание А↔В, степень истинности которого определяется выражением:
|
||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 416; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.90.141 (0.005 с.) |
 , где
, где 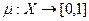 .
.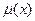 называется функцией принадлежности (к Х).
называется функцией принадлежности (к Х).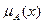 , заданной на множестве Х = {"ложь", "истина"}.
, заданной на множестве Х = {"ложь", "истина"}.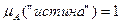 . Соответственно, ложное высказывание характеризуется функцией принадлежности
. Соответственно, ложное высказывание характеризуется функцией принадлежности 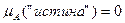 .
.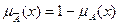 ;
;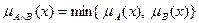 ; т.о. степень истинности нечеткого высказывания АÙВ определяется наименее истинным высказыванием;
; т.о. степень истинности нечеткого высказывания АÙВ определяется наименее истинным высказыванием;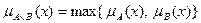 ; т.о. степень истинности нечеткого высказывания AÚB определяется наиболее истинным высказыванием;
; т.о. степень истинности нечеткого высказывания AÚB определяется наиболее истинным высказыванием; ;
;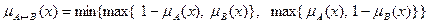 .
.


