
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проблема разрешимости логики предикатов.
1) Постановка проблемы: Существует ли алгоритм, который позволял бы по виду формулы логики предикатов судить о том, каков ее характер (например, тавтология это или формула всего лишь выполнима). Как доказано (в 1936 г., Черч), проблема имеет отрицательный ответ, т.е. логика предикатов неразрешима.
2) Причина неразрешимости состоит в наличии бесконечных предметных областей и, вообще говоря, различное поведение формулы на бесконечном и конечном множествах. Так, например, существует формула, выполнимая на бесконечном множестве, но не выполнимая ни на одном конечном множестве.
3) Однако при определенных «суждениях» логики предикатов, мы получаем разрешимость указанной проблемы. Так, например, если рассматривать только конечные предметные области М={ a1, a2,…..,am }, то в этом случае логика предикатов будет разрешимой. Это вытекает из следующей теоремы. Теорема. Для любого предиката Р(х) имеют место равносильности: (xР(х))ó(P(a1)/\P(a2)/\.../\P(am)) (1) ( Смысл утверждения в том, что кванторные операции на конечных множествах не являются состоятельными, а выражаются через логические связки /\, \/. Доказательство. Докажем (1), (2) – аналогично. Возможны случаи: а) Р(х) – тождественно истинен на М. В этом случае обе части (1) принимают значения истины. б) Иначе, для любого Р(х) есть ложное высказывание, но и в правой части (1) в составе конъюнкции есть «ложный компонент», т.е. конъюнкция есть ложь. В обоих возможных случаях получили высказывания одинакового значения истинности, чем и доказали равносильность (1). Теперь всякая формула на конечном множестве, согласно теореме (1), может быть «освобождена» от кванторных операций. Но в этом случае каждый входящий в формулу компонент на элементах конечного множества может реализоваться только как истина или ложь, а, значит, механизм таблицы истинности в случае конечного М оказывается применим, тем самым определяется характер формул, а, значит, положительно решена указанная проблема.
4) Оказывается, что и логика одноместных предикатов тоже разрешима, т.к. ограничившись лишь одноместными предикатами, мы можем проблему свести к случаю конечных множеств (без доказательства).
5) Итак, логика предикатов не противоречива в том смысле, что не может формула быть тавтологией и опровержимой (противоречием и выполнимой). Логика предикатов есть полная теория, т.е. каждая формула либо является тавтологией, либо опровержима. Наконец, она неразрешима, т.е. не существует единого соответствующего алгоритма. Однако это не означает, что для конкретной формулы нельзя отыскать приема для определения ее характера: просто этот прием будет применим к ней конкретно или к целому классу формул, но не ко всей логике в целом.
Понятие исчисления предикатов (ИП).
1) Синтаксис теории тот же, что и синтаксис логики предикатов. Синтаксис - алфавит и понятие формулы: Предметная переменная, предикатная переменная 0 местная, n – местная, логические связки, ┐,→ и символы Формула – это предикатная переменная, а так же если P и Q – формулы, то P→Q, 2) Аксиомы теории, которые принимаются как изначально выводимые формулы: а) Аксиомы ИВ; б) а также аксиомы (
3) Правило выводы других формул: А) ПЗ в ИВ; Б) Еще два правила: -Если B→P(x) выводимо, то B→( - Если B→P(x) выводимо, то (
4) Семантика – это наполнение теории конкретным содержанием, одной из возможных семантик является логика предикатов. Выводимость формулы в ЛП превращается в свойства ее тавтологичности. В частности, аксиомы ИП, применимые как выводимые формулы, в ЛП как легко проверить, оказываются тавтологиями. Правила вывода в ИП превращаются в ЛП в правила построения новых тавтологий.
5) Метатеория. а) ИП не противоречива; б) ИП полна, в том смысле, что каждая формула ИП либо выводима, либо не обладает этим свойством. в) ИП неразрешимая теория (иначе бы все ее семантики были неразрешимы, а это неверно в силу неразрешимости ЛП).
|
|||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 1700; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.172.252 (0.007 с.) |
 хР(х))ó(Р(a1) \/P(a2) \/...\/P(am)) (2)
хР(х))ó(Р(a1) \/P(a2) \/...\/P(am)) (2)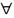 ,
, 


