Принцип логического программирования

 

Элементной базой современных цифровых устройств и систем являются цифровые интегральные схемы.

Цифровая интегральная схема– это микроэлектронное изделие, изготовленное методами интегральной технологии (чаще полупроводниковой), заключенное в самостоятельный корпус и выполняющее определенную функцию преобразования дискретных цифровых сигналов.

Для описания работы цифровых интегральных схем, а, следовательно, и устройств, построенных на их основе, используется математический аппарат алгебры высказываний. Возможность его применения для решения задач анализа и синтеза цифровых устройств обусловлена аналогией понятий и категорий этой алгебры и двоичной системы счисления, которая положена в основу представления преобразуемых устройством сигналов.

Простейшие преобразования над цифровыми сигналами осуществляют цифровые интегральные схемы, получившие названия логических элементов.

Определение 1.

Электронный логический элемент, реализующий отрицание в виде определенных уровней электрических сигналов, называют инвертором или логическим элементом “НЕ”.

Обозначения.

Вход логического элемента изображен слева, выход – справа. На выходной линии, в месте соединения ее с прямоугольником, изображается кружок – символ инверсии.

 

На языке цифровой техники инверсия означает, что выходной сигнал (у) противоположен входному (х). Сказанное можно проиллюстрировать временными диаграммами инвертора.

Определение 2.

Логический элемент, реализующий операцию конъюнкции, называют конъюнктором или логическим элементом “И”.

Обозначение.

Условное графическое изображение двухвходового (а) и трехвходового (б) конъюнкторов представлено на следующем рисунке:

Замечание.

Логический элемент “И” часто используют для управления потоком информации. При этом на один из его входов поступают сигналы, несущие некоторую информацию, а на другой – управляющий сигнал: пропустить информацию – 1, не пропустить – 0. Логический элемент “И”, используемый таким образом, называют вентиль.

На рисунке показаны возможные временные диаграммы двухвходового конъюнктора.

Определение 3.

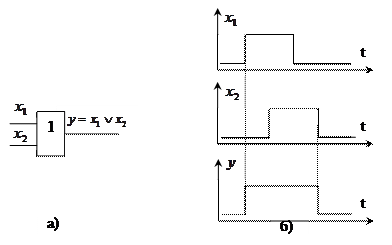
Логический элемент, реализующий операцию дизъюнкции, называют дизъюнктором или логическим элементом “ ИЛИ ”.

Условное изображение и временные диаграммы элемента “ИЛИ” приведены ниже.

Определение 4.

Комбинационным цифровым устройством называется устройство, выходные сигналы которого однозначно определяются лишь сигналами, действующими (в тот же момент времени) на его входах.

 

Комбинационные цифровые устройства применяются для выполнения целого ряда логических и арифметических преобразований над входными сигналами и используются в качестве шифраторов, дешифраторов, сумматоров, мультиплексоров и других функциональных узлов.

В общем случае проектируемое устройство может быть представлено в виде черного ящика, имеющего n входов и m выходов. Изначально об этом черном ящике известен лишь требуемый алгоритм его функционирования, т.е. характер связи между входными воздействиями и выходными сигналами (реакциями). Проектирование сводится к определению оптимальной структуры (схемы) цифрового устройства, реализуемой в заданном базисе логических элементов. Поскольку требуемый алгоритм функционирования, в общем случае, может быть реализован с помощью различных схем, то должна быть определена некоторая, оптимальная схема, например, схема, отличающаяся минимумом аппаратурных затрат, т.е. минимальным числом логических элементов.

 

Закон двойственности.

 

1) Операции /\ и \/ в алгебре высказываний называются двойственными.

F*(x₁,x₂, …, x_n) называется двойственной по отношению к F(x₁,x₂, …, x_n), если получение F* из F происходит путем однократной замены каждой операции \/, /\ на двойственную.

 

2) Способ получения из данной формулы двойственную, использующий только операции отрицания, содержится в следующей теореме.

Теорема 1: F(x₁,x₂,x₃,…x_n) ≡ ┐F*(┐ x₁,┐x₂,┐x₃,…┐x_n).

Доказательство:

1) Заметим прежде всего, что определение двойственности формулы предполагает, что все присутствующие в ней логические операции уже выражены только через \/ и /\, а операция отрицания относится только к пропозиционным переменным; это возможно в силу известных равносильностей и законов де Моргана.

2) Если рассматривать правую часть равносильности (1), то на основании законов де Моргана эту правую часть можно привести к равносильной форме, в которой произойдет:

а) замена в формуле F каждой операции на двойственную;

б) появление знака отрицания над каждым отрицаемым атомом, т.е., ┐x_j что равносильно x_j. В формуле F от аргумента x_j все операции заменены на соответствующие двойственные, а значит произведен переход к F*.

Замечание: В этом доказательстве используется очевидная симметричность соотношений двойственности: если F* двойственная к F, F двойственная к F* и верно обратное.

Теорема 2: Если F₁(x₁,x₂, …, x_n) ≡F₂(x₁,x₂, …, x_n) (2), то

F*₁(x₁,x₂, …, x_n) ≡ F*₂(x₁,x₂, …, x_n) (3), т.е. если две формулы равносильны, то двойственные им формулы равносильны.

Доказательство: Из условия следует, что ┐F₁≡ ┐F₂ , из предыдущей теоремы следует, что с учётом транзитивности F* отрицание ┐(┐F₁*(┐ x₁,┐x₂,┐x₃,…┐x_n))≡ ┐(┐F₂*(┐ x₁,┐x₂,┐x₃,…┐x_n)), по закону отрицания отрицания следует, что F₁*(┐ x₁,┐x₂,┐x₃,…┐x_n)≡ F₂*(┐x₁,┐x₂,┐x₃,…┐x_n), поскольку набор переменных (x₁,x₂,x₃,…x_n) (значений) произвольный, то будет произвольный и набор значений (┐ x₁,┐x₂,┐x₃,…┐x_n) обозначим y_{j ≡}x_j получаем: F₁*(y₁,y₂,y₃,…y_n)≡ F₂*(y₁,y₂,y₃,…y_n), т.е. из равносильности F₁ и F₂ получена равносильность двойственных формул.

Замечание. Очевидно, что соотношение двойственности обладает симметричностью, т.е. если F* двойственно к F, то F двойственно к F*.