
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие формулы алгебры высказыванияСтр 1 из 10Следующая ⇒
Алфавит алгебры высказываний (АВ). Рассмотрим совокупность некоторых объектов, которые будем называть высказываниями. Эти объекты будут обозначаться A, B или x, y, а сами символы будут называться пропозиционными переменными или атомами. Совокупность пропозиционных переменных обозначим G1. Алфавит есть множество, полученное объединениями 3 множеств: G=G1 U G2 U G3, где G2={┐, \/, /\} (логические связки), G3 – множество вспомогательных символов: скобки, запятые.
Любая упорядоченная конечная последовательность символов из алфавита называется словом.
Понятие формулы алгебры высказывания Среди всех слов выделяют формулы. Формула: а) Каждая пропозиционная переменная есть формула. б) Если A, B некоторые формулы, то слова ┐A, A\/B, A/\B – также формулы. в) Других формул в алгебре высказываний нет. Замечание: понятие формулы построено так называемым рекурсивным способом: на основе пропозиционных переменных строятся начальные формулы, затем на основе построенных новые формулы и т.д.
4) Cемантика:(содержательное направление) формула в случае атома есть высказование а в остальных случаях составное высказование.
Логические операции над высказываниями Наполним смыслом введенную выше символику. Будем называть высказыванием всякое повествовательное предложение, о содержании которого известно, истинно оно или ложно.
Отрицанием ┐P высказывания P называется новое высказывание, которое истинно тогда и только тогда, когда P ложно («не P»).
Операцией перехода от P к ┐P называется операция отрицания.
Дизъюнкцией P\/Q (“P или Q”) называется новое высказывание, которое истинно тогда и только тогда когда истинно хотя бы одно из высказываний. Переход от P и Q к их дизъюнкции называется операцией дизъюнкции.
Конъюнкция P/\Q (“P и Q ”) приводит к новому высказыванию, которое истинно тогда и только тогда, когда истинно и P и Q. Операция конъюнкции есть операция перехода от P и Q к новому высказыванию P/\Q.
В алгебре высказываний вводятся также еще 3 операции, которые на самом деле в дальнейшем будут выражены через уже введенные.
а) Импликация P и Q строится как новое высказывание P→ Q, которое ложно лишь в том случае когда P – истина, а Q – ложь. (“из P следует Q”).
б) Эквиваленция порождает новое высказывание
Истина тогда и только тогда, когда оба высказывания имеют одинаковый характер истинности.
в) Альтернативная дизъюнкция. (“или, или”).
Функции истинности. 1) Множество всех высказываний с введенными в нем результатами логических операций называют алгеброй высказываний (АВ).
2) На АВ вводится функция истинности λ, которая каждому высказыванию А сопоставляет значение
0, если А - ложно. В терминах значений функции истинности все таблицы истинности могут быть записаны как матрицы, состоящие из единиц и нулей, например:
Классификация формул алгебры высказываний. 1) Если для данной формулы f λ(f)≡1, то формула f называется тождественно-истинной или тавтологией. Обозначение: ├f. Пример: x\/┐x. Формула, не являющаяся тавтологией, называется опровержимой, то есть для опровержения формулы найдется такой набор переменных, что λ(f)=0. Пример: x\/x.
2) Формула f называется тождественно-ложной, если λ(f)≡0. Еще ее называют противоречие. Пример: x/\┐x Формула, не являющаяся тождественной ложью, называется выполнимой, то есть выполнение формулы F означает, что λ(F)=1. Класс формул выполнимых шире класса тавтологий.
Замечание: символы логических связок и понятия формул можно было бы использовать не «наполняя» понятия пропозиционных переменных конкретным смыслом высказывания, а понимая под этими переменными элементы произвольных множеств, над которыми можно производить 3 операции, обозначаемые: ┐, \/, /\. Если в заданном множестве введены такие элементы Е и Ø, для которых всегда верны свойства операций пункта 2, а также если верны свойства операций, изложенные в предыдущем параграфе (основные равносильности, где знак равносильности означает совпадение элементов), то заданное множество называют Булевой алгеброй.
Примерами Булевых алгебр являются алгебра высказываний (АВ) и алгебра множеств. Равносильные формулы.
1) Говорят что F1≡ F2 (равносильны), если λ(F1)≡λ(F2). Другими словами равносильные формулы на каждом наборе переменных принимают значение истины или лжи одновременно. Замечание: может случиться так, что количество переменных у одной из формул будет больше, чем у другой. В этом случае F1≡ F2 тогда и только тогда, когда значения истинности формулы, с большим количеством переменных определяется значениями только значениями функции, с меньшим числом переменных.
2) Свойства отношения равносильности: а) рефлексивность: F≡ F. б) симметричность: если F1≡ F2 , то F2≡ F1. в) транзитивность: если F1≡ F2, F2≡ F3, то F1≡ F3. Эти свойства очевидны, если воспользоваться определением равносильности через значения функции истинности. Критерий равносильности 1) Теорема: F≡G тогда и только тогда, когда |–(F↔G) Доказательство: Если F≡G, то на каждом наборе переменных значения истинности этих двух формул будут одинаковы, то есть они одновременно истинны или одновременно ложны. Но в этих случаях эквиваленция принимает только значения истины. Если наоборот, эквиваленция есть тавтология, то на любом наборе переменных одновременно истинны или одновременно ложны F и G, а это как раз означает их равносильность
Основные понятия исчисления высказываний (ИВ). Выводимость из группы формул.
1) ИВ есть аксиоматическая теория, которая позволяет все вышеприведенные утверждения сформулировать и доказать на основе систем основных понятий, минимального количества аксиом и правил вывода (получения) новых утверждений. Синтаксис: а) Алфавит ИВ содержит пропозиционные переменные и две операции: операция ┐(относится к 1 переменной) и операция → (соединяющая 2 пропозиционные переменные). б) Слово в ИВ есть любой упорядоченный конечный набор символов алфавита. в) Понятие формулы: 1. Всякая пропозиционная переменная есть формула. 2. Если Р – формула, Q – формула. то ┐Р, P→Q также формулы. 3. Других формул в ИВ нет. Замечание. Вспомогательные символы, т.е. запятые, скобки употребляются так же как в АВ.
2) Основным понятием в ИВ является понятие выводимой формулы (доказуемой формулы) ├Р.
3) Система аксиом - это система договоренности о том, какие формулы в данной теории заранее принимаются выводимыми. В ИВ утверждаются аксиомы: 1. ├P→(Q→P); 2. ├(P→(T→Q))→((P→T)→(P→Q)); 3. ├(┐P→┐Q)→((┐P→Q) →P).
4) Единственным правилом вывода в ИВ является ПЗ (правило заключения): если ├P и ├(P→Q), то ├Q.
5) Теорема 1. Если ├R, то ├(B→R), где В – любая формула. Доказательство. Из первой аксиомы получаем ├R→(B→R); R выводима по условию, на основании ПЗ получаем ├(B→R). Теорема 2. Для любой формулы В имеет место ├(В→В). Теорема вытекает из второй аксиомы, записанной в более общем виде.
1) Это понятие обобщает понятие логического следования из группы формул, но оно уже не может использовать известные в АВ логические операции.
Пусть имеется группа формул {Г} в ИВ. Формула В – выводима из Г, если существует такая последовательность В1, В2, …, Вn-1, Вn, то: а) Вn≡В (совпадение формул); б) Каждая формула Вj в этой последовательности либо из набора {Г}, либо аксиома, либо получена из двух предыдущих по правилу заключения (ПЗ). Последнее надо понимать так: в указанной последовательности имеется последовательность Вj-1, Вj-1→Вj, Вj.
2) Набор {Г} вообще говоря бесконечен. Теорема 1. Если множество {Г} является подмножеством {Δ} и ({Г}с{ Δ }). Если В выводим из {Г}, то В выводим из {Δ}. Утверждение очевидно, поскольку те формулы последовательности Вj, которые были взяты из {Г} являются одновременно взятыми из {Δ}.
3) Обозначения выводимости из группы формул: {Г}├В. В определении выводимости не исключалось также, что набор {Г} пуст; то, что тогда представляет собой определение выводимости из {Г} есть просто выводимость в исчислении, т.к. В получается тогда лишь из аксиом ПЗ. В этом случае ├В. Говорят также, что В доказуемо или теорема в ИВ. Все элементы множества {Г} называют гипотезами при выполнении которых выводима В. А последовательность В1, В2, …, Вn-1, Вn называют также выводом формулы В.
4) Нельзя ли свести определения выводимости к конечному набору гипотез? Утвердительный ответ содержится в следующей теореме. Теорема. Соотношение {Г}├В (1) имеет место тогда и только тогда, когда найдется конечный набор гипотез H1, H2,…, Hm из {Г}, такой, что { H1, H2,…, Hm}├B. (2) Доказательство. Если (2) имеет место, то (1) имеет место по теореме пункта 2, поскольку набор {Г} более широк, чем набор Hj. Обратно. Если имеет место (1), то В является конечным звеном цепочки формул В1, В2, …, Вn-1, В. (3) Среди формул, предшествующих В может быть только лишь конечное количество гипотез, взятых из {Г} (понятно, что и сама В может быть такой же гипотезой). Именно этот конечный набор, участвующий в выводе и представляет собой ту самую последовательность H1, H2,…, Hm о которой шла речь в выводе (2). Суть теоремы в том, что можно без ограничения общности считать, что {Г} есть конечное множество. Теорема дедукции в АВ.
Если (H, G)├F, (1) то H├(G→F). (2) Доказательство согласно критерию следования (H/\G)├F. В этом случае F не ложно, когда G и H истинны. Если предположить, что (2) не имеет места, то это означало бы, что λ(F)=0, тогда как λ(H)=1 и λ(G)=1 (только в этом случае импликация принимает значение лжи), однако одновременно выполнение последних соотношений в силу условия (1) невозможно, что и доказывает утверждение (2).
Теорема дедукции в общем случае. Если (H1, H2, …, Hn)├ F, (3) то (H1, H2, …, Hn-1)├(Hn→F). (4) Суть в том, что одну из посылок можно сделать посылкой импликации, которая будет логически следовать из остальных посылок. Доказательство. Согласно критерию логического следования из группы формул соотношение (3) имеет место тогда и только тогда, когда (H1/\H2/\ …/\Hn)├ F. (5)
В Отношение (6) приняло вид (В/\Hn)├ F. Согласно все тому же критерию, оно равносильно (В, Hn)├ F. (7) По теореме 1 (и ситуации 1), тогда имеет место В├(Hn→F) или (H1/\H2/\ …/\Hn-1) ├(Hn→F). (8) Согласно критерию (8), это все равно, что (4). Итак, логическое следование (3) означает, что верно (4), а это и следовало доказать. Согласно теореме дедукции, которая записана в виде (4), можно проводить дальнейшее «отрывание» посылок. То есть, если дано (3), то в силу (4) справедливо следование (H1, H2, …, Hn-2)├(Hn-1→(Hn→F)). (9) Процесс можно продолжать и далее, пока все посылки не закончатся. Следствие. Если имеет место логическое следование (3), то следующая формула является тавтологией: ├(H1→(H2→ (Hn-1→(Hn→F)))). На ИВ 1) Пусть {H1, H2,…, Hm-1, Hm} ├ P, тогда {H1, H2,…, Hm-1} ├ (Hm→ P).
2) Следствие. ├(H1 →(H2 →…→ (Hm-1→(Hm→ P))…)), если выполнено условие теоремы пункта 1. Следствие доказывается последовательным применением теоремы пункта 1 (последовательным отщеплением гипотез H1, H2,…, Hm-1, Hm.). Выводимость (H1, H2,…, Hn-1, Hn) ├ P (1) имеет место тогда и только тогда, когда справедлива выводимость (H1, H2,…, Hn-1)├(Hn→ P). (2) Тот факт, что из (1) следует (2), утверждается в пункте 1. Установим обратное. Выводимость (2) означает, что нашелся набор формул (вывод) В1, В2,…,Вn-1 (Hm→ P), (3) Причем, среди формул Вj возможно присутствуют какие-то из гипотез Hk (k=1 2,…,m-1) Поскольку множество гипотез можно расширять согласно предыдущему параграфу, то и последовательности (3) можно добавить гипотезу Hm: В1, В2,…,Вm-1 Вm, (Hm→ P). (4) Теперь можно считать, что (4) есть вывод для Р, поскольку Р будет получаться по ПЗ. В1, В2,…,Вm-1 Вm, (Hm→ P), Р. (5) Итак, (5) есть вывод Р. Из чего? – из набора H1, H2,…, Hm-1, в который добавлено Hm (а остальные участники (5) могут быть аксиомы или результаты ПЗ). Итак, получили выводимость Р из H1, H2,…, Hm-1, Hm, т.е. доказано (1)
4) Имеет место выводимость {P, P→Q,Q→T} ├ {P→T} (6) («транзитивность импликации»). Доказательство. Мы в праве дополнить формулу P, P→Q,Q→T еще одной формулой, а именно Q, т.е. записать в качестве гипотез набор вида P, P→Q,Q, Q→T (7). Рассмотрим (7), как последовательность-вывод формулы Т, поскольку она (Т) есть результат ПЗ: P, P→Q,Q, Q→T, Т, т.к. Т - завершающая формула, то можно записать P, P→Q,Q, Q→T├Т. На основании теоремы дедукции любую гипотезу, в частности Р, можно «отщепить», кроме того в наборе посылов можно снова исключить Q, поскольку она не была самостоятельной посылкой, а результатом ПЗ.
{P→Q,Q→T} ├ (P→T) (8). Итак, установлено (8), а значит и (6) (поскольку Р можно добавить в перечень гипотез).
Формулы логики предикатов. 1) Алфавит состоит из объединения множеств следующих символов: а) Символы предикатных переменных (х, у, …, x1, x2, …, xn …); б) Символы 0-местных предикатных переменных P, Q, … в) Символы n-местных предикатных переменных P, Q, … г) Символы логических операций ┐, /\, \/, →, ↔; д) Символы кванторных операций , 2) Формулы: а) По определению 0-местныя предикатная переменная (формула); б) Результат подстановки на свободные места различных предметных переменных в n-местную предикатную переменную, т.е. Р(x1,x2,…,xn) есть формула, все указанные предметные переменные в этой формуле называются свободными. в) Если переменная xj в формуле Р(x1,x2,…,xn) свободна, тохjР(x1,x2, xj,…,xn) – формула. Все переменные, которые были свободны в формуле Р кроме хj остаются в полученной формуле свободными, а переменная хj теперь называется связанной. Могло быть так, что в формуле Р до применения связываний по хj уже были связанные переменные. Они остаются связанными и в полученной формуле. г) Если Р – формула, то ┐Р – также формула, причем все переменные, которые были свободны, остаются такими же в полученных формулах. д) Если P и Q формулы, то P/\Q, P\/Q также формулы. При этом те предметные переменные, которые были свободны в P и Q, остаются такими же в полученных формулах. е) Других формул нет. 3) Интерпретация формул. Рассмотрим теперь конкретное множество М значений предметной переменной х=(x1,x2,…,xn) и формулу F, которая на М определяется только для указанных х. Если на место каждой предикатной переменной, участвующей в F, записать конкретный предикат (в нем столько же мест, сколько переменных), то получим конкретный предикат на М. Если теперь выбрать и зафиксировать х, то предикат превратится в высказывание. Это и называется интерпретацией формулы F. Ясно, что всевозможных интерпретаций каждой формулы может быть бесконечно много. Теперь, чтобы доказать какое-либо утверждение о формулах достаточно его доказывать для результата подстановки в нее произвольных предикатов на места предикатных переменных. Классификация формул. 1) Формула называется тождественно истинной на М, если всякая ее интерпретация есть истина, иначе она опровержима. 2) Формула тождественно ложна на М, если всякая ее интерпретация является ложью. 3) Формула является тавтологией, если она тождественно истинна на каждой предикатной области М. 4) Формула является противоречием, если она будет тождественной ложью на каждой предметной области М. 1) Пусть дана предметная область М, формулы F и G на М. Говорят, что на М формулы F и G равносильны и записывают F ≡ G (на М), если при подстановке в формулы F и G на место предикатных переменных конкретных предикатов, получаются всякий раз равносильные на М предикаты. Другими словами, соответствующие интерпретации формул F и G на каждом элементе из М совпадают.
2) Говорят, что F и G равносильны, если они равносильны на всякой предметной области М и записывают F ≡ G.
3) Теорема. F ≡ G тогда и только тогда, когда эквиваленция F↔G является тавтологией. Доказательство очевидно. Тавтология означает, что всегда интерпретация формул F и G является истинным высказыванием или ложным высказыванием одновременно, но тогда их интерпретации совпадают, что равносильно F ≡ G. Эта теорема дает нам готовый набор равносильных формул, если воспользоваться уже доказанными тавтологиями. Пример. (x(Р(х) \/В))≡((x(Р(х) \/В), где В – предикатная переменная, либо 0-местная, либо с произвольным количеством мест, но среди свободных в ней переменных не должен содержаться х.
4) Очевидно, что соотношение равносильности обладает свойствами рефлексивности, симметричности и транзитивности (следует из определения).
5) Равносильными называются такие преобразования формулы F, которые приводят к формуле, равносильной F. В силу транзитивности соотношения равносильности, мы можем выполнить цепочку равносильных преобразований, получая всякий раз формулу, равносильную предыдущей. В итоге исходная и заключительная формулы оказываются равносильными.
Закон двойственности.
1) Операции /\ и \/ в алгебре высказываний называются двойственными. F*(x1,x2, …, xn) называется двойственной по отношению к F(x1,x2, …, xn), если получение F* из F происходит путем однократной замены каждой операции \/, /\ на двойственную.
2) Способ получения из данной формулы двойственную, использующий только операции отрицания, содержится в следующей теореме. Теорема 1: F(x1,x2,x3,…xn) ≡ ┐F*(┐ x1,┐x2,┐x3,…┐xn). Доказательство: 1) Заметим прежде всего, что определение двойственности формулы предполагает, что все присутствующие в ней логические операции уже выражены только через \/ и /\, а операция отрицания относится только к пропозиционным переменным; это возможно в силу известных равносильностей и законов де Моргана. 2) Если рассматривать правую часть равносильности (1), то на основании законов де Моргана эту правую часть можно привести к равносильной форме, в которой произойдет: а) замена в формуле F каждой операции на двойственную; б) появление знака отрицания над каждым отрицаемым атомом, т.е., ┐xj что равносильно xj. В формуле F от аргумента xj все операции заменены на соответствующие двойственные, а значит произведен переход к F*. Замечание: В этом доказательстве используется очевидная симметричность соотношений двойственности: если F* двойственная к F, F двойственная к F* и верно обратное. Теорема 2: Если F1(x1,x2, …, xn) ≡F2(x1,x2, …, xn) (2), то F*1(x1,x2, …, xn) ≡ F*2(x1,x2, …, xn) (3), т.е. если две формулы равносильны, то двойственные им формулы равносильны. Доказательство: Из условия следует, что ┐F1≡ ┐F2 , из предыдущей теоремы следует, что с учётом транзитивности F* отрицание ┐(┐F1*(┐ x1,┐x2,┐x3,…┐xn))≡ ┐(┐F2*(┐ x1,┐x2,┐x3,…┐xn)), по закону отрицания отрицания следует, что F1*(┐ x1,┐x2,┐x3,…┐xn)≡ F2*(┐x1,┐x2,┐x3,…┐xn), поскольку набор переменных (x1,x2,x3,…xn) (значений) произвольный, то будет произвольный и набор значений (┐ x1,┐x2,┐x3,…┐xn) обозначим yj ≡xj получаем: F1*(y1,y2,y3,…yn)≡ F2*(y1,y2,y3,…yn), т.е. из равносильности F1 и F2 получена равносильность двойственных формул. Замечание. Очевидно, что соотношение двойственности обладает симметричностью, т.е. если F* двойственно к F, то F двойственно к F*.
Алфавитный оператор.
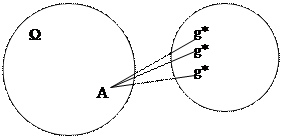
1) Алфавит G – конечное множество символов произвольной природы, а слово g – упорядоченное множество (конечная последовательность символов алфавита, при этом символы в слове могут повторяться).
2) Пусть даны два алфавита G и G*. Алфавитным оператором А, определенным на множестве Ω слов алфавита G, называется соответствие, которое каждому символу gєΩ сопоставляет одно или несколько слов в алфавите G*. Слово g* (слова g*) называют образами слова g. Множество Ω называется областью определения алфавитного оператора А, а множество всевозможных получаемых в результате действия оператора А образов Ω* называется областью значений оператора А.
В этом определении оператор А может быть как однозначным, так и многозначным.
3) Если оператор А однозначный и различным прообразом g соответствуют различные g*, то существует однозначный обратный оператор А А -1:g* ׀→ g. Его область определения служит Ω*, а множество значений будет Ω.
4) К понятию алфавитного оператора тем или иным способом можно свести практически любые способы преобразования информации, а значит, об алгоритмах можно теперь говорить как о способах задания алфавитных операторов. Слова исходного алфавита G часто называют входными, а их образы – выходными словами. Часто рассматривают случай G ≡ G*. Тогда говорят, что оператор А действует в алфавите G. Поскольку алфавитный оператор есть очень общее понятие, включающее в себя очень многие объекты (например, функции в математике), то и способы его задания, т.е. способы преобразования входных в выходные могут быть самыми разными. Важно только, чтобы за конечное количество шагов каждое входное слово было преобразовано в выходное (выходные). Такими способами могут быть: а) В случае конечного набора Ω и конечно-значного оператора таблица
б) Посимвольное отображение, т.е. задан способ по которому каждый символ αєG соответствовал единственный символ βєG*. В этом случае каждому слову gєΩ соответствует единственное слово g*єΩ*, которое состоит из каждого символа, входящего в g. в) Кодирующее отображение. Здесь каждому символу αєG соответствует конечная последовательность символов алфавита G* - так называемый код. α |→β1, β2, …, βk. В этом случае набор кодов определяет для каждого gєΩ соответствующее слово g*єΩ*. г) Другие способы. Теорема Тьюринга.
Теорема Тьюринга. Классы всех вычислимых по Тьюрингу и рекурсивных функций совпадают. Примеры алгоритмов: 1. Сконструировать машину Тьюринга, вычисляющую функцию следования S(x)=x+1.
Программа должна быть устроена таким образом, чтобы на месте какого-то нуля она написала 1 и остановилась. Для определенности выберем положение головки на крайней правой ненулевой ячейке. q11→q11(Л) … q10→q11 В результате появилась еще 1 единица, т.е. число увеличилось на единицу, а значит, функция следования вычислена. Итак, на примере функции следования показано, что рекурсивная функция просчитана на соответствующей машине Тьюринга. Верно и обратное: указанная машина для всякого записанного на ленте слова производит увеличение соответственного числа на единицу, т.е. вычисляет функцию следования.
3) Пример словесного алгоритма: Вычислить произведение вида А=∏aj. 1. Присвоить А значение 1 (А=1), перейти к п.2. 2. j=1, перейти к п.3. 3. А=А aj, перейти к п.4. 4. Если j=n, то п.3. – ответ, иначе если j<n, то j=j+1, перейти к п.3. Машина Тьюринга(МТ). 1) Машина Тьюринга – это алгоритмическая система, реализующая алфавитный оператор.
б) В каждый момент на ленте машины записано одно и только одно слово. в) Все остальные ячейки ленты заполнены «пустым символом» (a0). г) В каждый момент машина обозревает одну и только одну ячейку. Условно говорят, что считывающая головка находится над этой ячейкой. д) Имеется также так называемый алфавит внутренних состояний Q = {q0, q1, …, qm,….}и в каждый момент при обозрении определенной ячейки машина находится в некотором состоянии qj. Так, например, обозревая ячейку с символом ak в состоянии qi, запишем qiak.
2) Как работает машина Тьюринга: Задается программа, т.е. система команд вида qiak → qjal(S) (1) Каждая команда (1) означает, что обозревая ячейку ak в состоянии qi, машина стирает символ ak и записывает в эту ячейку символ al (возможно, что k=l). После этого машина переходит в состояние qj и затем со считывающей головкой происходит процесс S, а именно, либо головка передвигается на одну ячейку вправо, что обозначается символом П, либо влево (Л), лтбо головка остается на прежнем месте, что обычно не обозначают никаким символом. Принято обозначать первую команду символом q1, а завершающую символом q0, так что в команде 1 i≠0. Итак, задано слово, задано начальное положение головки (как правило задано) и задана программа, т.е. система команд вида (1), среди которых самая первая начинается с символа q1. Выполняя последовательно указанные команды, машина преобразует каждый символ заданного слова в другой или этот же символ до тех пор, пока не придем к команде вида (1), в которой j=0. На этом преобразование слова завершается, и мы получаем выходное слово в том же алфавите.
3) Машина Тьюринга есть условная машина; это математический объект, который реализует действия алфавитного оператора; можно считать его прообразом реальных вычислительных машин, в которых на самом деле количество ячеек конечное, и программы записываются по вполне определенным законам.
4) Как же вычисляет арифметические операции машина Тьюринга? Пусть имеется функция n-переменных y=f(x1, x2,…,xn), где все xjÎZ+. В этом случае в качестве алфавита внешних символов можно задать алфавит G={0,1}, где 0-пустой символ. На ленте машины записывается любой xj в виде стольких последовательностей единиц, число которых равно xj. Пробелы между двумя соседними наборами единиц (двумя соседними аргументами) могут быть обозначены заданным количеством нулей. В результате каждое написанное слово будет означать вектор x =(x1, x2,…,xn). Теперь начинается действие программы. Считая вычислимую функцию однозначной, мы получаем в результате некоторый набор единиц, который и будет составлять число y. Замечание. Один из возможных способов записи аргументов, включая нулевое значение, состоит, например, в том, что аргументу 0 соответствует 1, аргументу xj >0 соответствует количество единиц xj+1. В этом случае робел можно обозначить одним нулем. Возникает вопрос о том, каждая ли арифметическая функция может быть вычислена с помощью подходящей машины Тьюринга. Каждая вычислимая этим образом арифметическая функция называется вычислимой по Тьюрингу. Тезис Тьюринга: всякая вычислимая арифметическая функция есть функция, вычислимая по Тьюрингу.
Тезис Тьюринга есть некоторая гипотеза, подтверждаемая примером всех имеющихся в практике вычислимых функций. Он не может быть доказан, поскольку само понятие алгоритма является первоначальным, т.е. строго неопределенным. Теоретически он мог бы быть опровергнут, если бы нашелся пример функции вычислимой, но не вычислимой ни на какой машине Тьюринга.
Основные понятия нечёткой логики. Нечёткие множества. Определение 1. Пусть задано некоторое непустое множество Х. Нечетким называется множество A, определенное как множество пар вида: Множество Х называется базовым множеством, а функция Замечание 1. Значения функции принадлежности формируются субъективно и могут иметь различный вид для одного и того же субъекта при различных обстоятельствах и настроениях. Определение 2. Высказывание A называется нечетким, если допускается, что оно может быть одновременно истинным и ложным (что определяется различными обстоятельствами и настроениями). Любое оценочное суждение, основанное на неполных или недостоверных данных, является нечетким и сопровождается обычно выражением степени уверенности (или сомнения) в его истинности. Например, утверждение: "Скорее всего, завтра похолодает". Определение 3. Мера (степень) истинности нечеткого высказывания A определяется функцией принадлежности Замечание 2. Четкое истинное высказывание характеризуется функцией принадлежности
Нечеткие высказывания могут быть простыми и составными. Составные высказывания образуются из простых с помощью логических операций, называемых также логическими связками. 1) Результатом отрицания нечеткого высказывания A называется нечеткое высказывание Ā (A), степень истинности которого определяется выражением: 2) результатом конъюнкции нечетких высказываний A и B называется нечеткое высказывание АÙВ, степень истинности которого определяется выражением: 3) дизъюнкция нечетких высказываний A и B приводит к нечеткому высказыванию AÚB, степень истинности которого определяется выражением: 4) степень истинности «нечеткой импликации» А→В нечетких высказываний A и B определяется выражение: 5) эквиваленция нечетких высказываний A и B приводит к нечеткому высказывание А↔В, степень истинности которого определяется выражением: Алфавит алгебры высказываний (АВ). Рассмотрим совокупность некоторых объектов, которые будем называть высказываниями. Эти объекты будут обозначаться A, B или x, y, а сами символы будут называться пропозиционными переменными или атомами. Совокупность пропозиционных переменных обозначим G1. Алфавит есть множество, полученное объединениями 3 множеств: G=G1 U G2 U G3, где G2={┐, \/, /\} (логические связки), G3 – множество вспомогательных символов: скобки, запятые.
Любая упорядоченная конечная последовательность символов из алфавита называется словом.
Понятие формулы алгебры высказывания Среди всех слов выделяют формулы. Формула: а) Каждая пропозиционная переменная есть формула. б) Если A, B некоторые формулы, то слова ┐A, A\/B, A/\B – также формулы. в) Других формул в алгебре высказываний нет. Замечание: понятие формулы построено так называемым рекурсивным способом: на основе пропозиционных переменных строятся начальные формулы, затем на основе построенных новые формулы и т.д.
4) Cемантика:(содержательное направление) формула в случае атома есть высказование а в остальных случаях составное высказование.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 2346; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.125.171 (0.206 с.) |
 λ(А)= 1, если А - истинно,
λ(А)= 1, если А - истинно, Согласно свойству ассоциативности, это означает, что ((H1/\H2/\ …/\Hn-1) /\Hn)├ F. (6)
Согласно свойству ассоциативности, это означает, что ((H1/\H2/\ …/\Hn-1) /\Hn)├ F. (6) .
.
 Сконструировать – значит ввести внешний алфавит и записать программу. А={0,1}. Поскольку х – целое неотрицательное число, то на ленте машины можно записать столько единиц, чтобы их сумма составляла х (если х=0, то не писать ничего, пустые ячейки заполнены нулями).
Сконструировать – значит ввести внешний алфавит и записать программу. А={0,1}. Поскольку х – целое неотрицательное число, то на ленте машины можно записать столько единиц, чтобы их сумма составляла х (если х=0, то не писать ничего, пустые ячейки заполнены нулями). а) Имеется так называемый внешний алфавит G={ a0, a1,…..,an}, символы которого, сформированные в слов, записываются в соседних ячейках некоторой бесконечной в обе стороны ленты.
а) Имеется так называемый внешний алфавит G={ a0, a1,…..,an}, символы которого, сформированные в слов, записываются в соседних ячейках некоторой бесконечной в обе стороны ленты. , где
, где 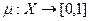 .
.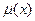 называется функцией принадлежности (к Х).
называется функцией принадлежности (к Х).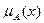 , заданной на множестве Х = {"ложь", "истина"}.
, заданной на множестве Х = {"ложь", "истина"}.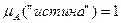 . Соответственно, ложное высказывание характеризуется функцией принадлежности
. Соответственно, ложное высказывание характеризуется функцией принадлежности 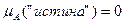 .
.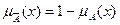 ;
;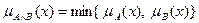 ; т.о. степень истинности нечеткого высказывания АÙВ определяется наименее истинным высказыванием;
; т.о. степень истинности нечеткого высказывания АÙВ определяется наименее истинным высказыванием;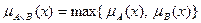 ; т.о. степень истинности нечеткого высказывания AÚB определяется наиболее истинным высказыванием;
; т.о. степень истинности нечеткого высказывания AÚB определяется наиболее истинным высказыванием; ;
;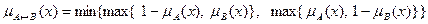 .
.


