
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Визначення коефіцієнта тертя кочення
Мета роботи:
Обладнання: користуючись установкою РМ-07 визначити коефіцієнт тертя кочення.
установка РМ-07.
коефіцієнт тертя кочення 8. Рисунок 9.1
Теоретичні відомості
Сили, що проявляються при відносному переміщенні дотичних тіл одного відносно іншого називається силами зовнішнього тертя. Розрізняють сили тертя спокою, кочення і ковзання. При невеликих швидкостях сила тертя не залежить від швидкості тіла і визначається за формулою Кулона
F = kN, (9.1)
де k — коефіцієнт тертя ковзання, N — сила нормального тиску. Сила тертя кочення також визначається формулою Кулона
де k — коефіцієнт тертя кочення, N — сила нормального тиску, r – радіус тіла яке котиться. Коефіцієнт тертя кочення можна визначити за допомогою установки РМ-07.
F H підставка 8, нахилені під кутом mgsin β до горизонту, то на кульку в стані спокою діє сила тяжіння mg mg, сила натягу нитки F ні сила
нею на роботу проти сил тертя. Якщо за n коливань енергія кульки зменшилась на ∆Е, то робота, виконана кулькою проти сил тертя, дорівнює
A = D E. (9.3)
Робота, як відомо А=FS, де F— сила тертя кочення, S— шлях, пройдений кулькою за n коливань. Використаємо значення F з рівняння (9.2). Вираз для роботи набере вигляду
Порівнюючи (9.3) і (9.4), можна записати, що
З цього рівняння можна визначити k, якщо всі інші величини відомі. Цілях S можна визначити як середнє значення шляху, пройденого кулькою за одне коливання < S >, помножено на число коливань, тобто
S=<S>n. (9.6)
З рис. 9.3 видно, що шлях, пройдений кулькою за одне коливання, дорівнює
C’ го коливання і кількість коливань. Вимірявши, штангенциркулем,
CA’
h
AD
Рисунок 9.4 діаметр кульки, визначимо, її радіус. Сила реакції опори, як видно з рис. 9.2, дорівнює N = mg cos b. Залишилось
AC=l (1 -cosα), і, відповідно, h=l( 1 -cosα)sinβ.
Таким чином, кулька відхилена від положення рівноваги на кут α, має потенціальну енергію
D E = mgl sin b 1 - cos a 1 - 1 - cos a 2. (9.9)
1 2
(при перетворенні вважати, що при малих кутах α, sinα = α). Підставивши значення зміни енергії, сили реакції
кочення потрібно виміряти діаметр кульки, кути відхилення нитки, кількість коливань і кут нахилу нитки до горизонту.
Порядок виконання роботи
1. Натиснути кнопку "сеть” і перевірити чи всі індикаторні лампочки висвічують цифру нуль. 2. Нахилити стержень 2 під кутом 60° до горизонту. 3. Відхилити нитку з кулькою на кут 10-15˚. 4. Відпустити кульку і одночасно натиснути кнопку "сброс". 5. Коли кут відхилення досягне величини 3-4°, натиснути кнопку "стоп”. 6. Виміряти штангенциркулем діаметр кульки. 7. Дослід повторити 5-6 разів. 8. Для кожного випадку обчислити за формулою (9.12) значення k. Обчислити похибки згідно вказівок.
Контрольні запитання
1. Які сили називають силами тертя? 2. Які є види тертя? 3. Формули Кулона для сил тертя. 4. Від чого залежить коефіцієнт тертя?
Лабораторнаробота№10
ВИВЧЕННЯ ПРЕЦЕСІЇ ГІРОСКОПА
Мета роботи:
Обладнання: переконатись на досліді в існуванні гіроскопічного ефекту і встановити від чого залежить кутова швидкість прецесії гіроскопа.
установка РМ-10.
1 2
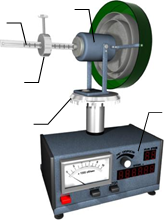
Установка РМ-10 складається з гіроскопа, який приводиться в рух електродвигуном 1, коромисла з поділками 2, противаги 3, диска з градусними поділками 4, електронного блоку відліку кута, часу і кількості обертів двигуна 5.
У кожному тілі є три взаємно перпендикулярні осі обертання, що Рисунок10.1 проходять через центр мас, які, при відсутності дії зовнішніх сил, не змінюють своєї орієнтації в просторі. Такі осі називаються головними осями інерції. Обертання тіла навколо осей з найбільшим і найменшим моментом інерції є стійким, а обертання навколо вісі з проміжним значенням моменту інерції — нестійким. Властивість головних осей зберігати своє положення в просторі широко використовується в техніці, зокрема, в гіроскопі. Гіроскоп — масивне однорідне тверде тіло, яке-обертається з великою кутовою швидкістю навколо однієї з
головних осей інерції, яка є і віссю симетрії. Для гіроскопів
O’’ тому, що, коли на гіроскоп, який обертається навколо вісі
O’’ гіроскоп навколо іншої вісі О'О', то гіроскоп повернеться навколо третьої вісі О"О",
має момент імпульсу L. Подіємо на цей гіроскоп парою сил F 1, і F 2так, щоб момент цих сил намагався повернути гіроскоп навколо вісі О'О'. Момент цих сил напрямлений вздовж вісі О'О'. Поява моменту сил М викличе зміну моменту імпульсу dL = Mdt. Напрям dL буде такий же, як і момент М. Результуючий момент імпульсу гіроскопа буде L ΄. Таким чином, для того, щоб гіроскопу мати цей момент імпульсу, він повинен повернутися навколо вісі О"О", яка перпендикулярна до осей ОО і О'О'. Якщо на гіроскоп діяти тривалий час сталим за напрямком моментом М, то вісь гіроскопа займе таке положення, що і вісь і напрям власного обертання співпадуть з напрямом і віссю обертання під дією моменту зовнішніх сил.
Тепер розглянемо гіроскоп, який обертається навколо вісі, що відхилена від вертикалі на кут α і закріплена в точці О (рис. 10.3). На гіроскоп діє сила тяжіння mg, яка намагається повернути гіроскоп навколо вісі О'О'. Гіроскоп, під дією цієї сили, одержить додатковий момент імпульсу dL напрям якого
співпадає з віссю О'О'. В результаті чого гіроскоп повертається на кут dφ (гіроскопічний ефект). В новому положенні момент сили mg, знову буде перпендикулярний до вісі гіроскопа, і знову гіроскоп буде повертатись з нового положення на кут dφ за час dt і так далі. Таким чином, вісь гіроскопа буде обертатися навколо вісі ОО, описуючи в просторі конус. Такий рух називається прецесією.
Рисунок10.3 вище сказане, визначимо кутову швидкість прецесії гіроскопа, а саме:
при сталій кутовій швидкості гіроскопа.
Рисунок10.4 великою кутовою швидкістю навколо вісі
противаги можна відхилити вісь гіроскопа від горизонтального положення, але на це потрібно звертати увагу, бо, як показано вище, швидкість прецесії не залежить від кута нахилу вісі гіроскопа.
Порядок виконання роботи
1. По рівню, переконатись, що гіроскоп знаходиться в горизонтальному положенні. 2. Натиснути на кнопку „сеть” і перевірити чи світяться індикаторні лампочки. 3. В момент часу, коли одна з поділок диска, що відповідає десяткам градусів, стане проти стрілки, натиснути кнопку „сброс”. Після цього, як у віконечку з’явиться цифра 17, натиснути на кнопку „стоп”. Відлік часу припиняється тоді, коли на віконечку появиться цифра 18. Це означає, що зафіксовано час повороту диску на 180˚. 4. Встановити противагу на коромислі на поділці 1см. Ввімкнути електродвигун і довести, за допомогою потенціометра, кількість обертів двигуна до 6000 обертів. 5. Пересувати противагу, кожний раз на 1см. Повторити досліди для різних значень х, при цьому звернути увагу на напрям обертання. Вважати напрям обертання за годинниковою стрілкою додатнім, а проти — від’ємним.
7. Побудувати графік залежності ω΄ від х. 8. За точкою перетину графіка з віссю х знайти положення противаги, при якому ω = 0. Поставити противагу в це положення і переконатись, що процесія відсутня.
Контрольні запитання
1. Що називається моментом інерції матеріальної точки і твердого тіла відносно заданої вісі? 2. Що називається моментом імпульсу точки і твердого тіла? 3. Що називається моментом сили? 4. Який зв’язок між моментом сили і моментом імпульсу? 5. Що називається гіроскопом? 6. В чому полягає гіроскопічний ефект? 7. Що називається прецесію гіроскопа?
Лабораторнаробота№11
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 625; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.112.220 (0.099 с.) |




 Установка РМ-07 складається з електронного блока вимірювання часу і кількості коливань 1, стержня 2, нитки 3, кульки 4, фотоелектричного датчика 5, шкали для вимінювання кута відхилення нитки 6, шкали для вимірювання кута відхилення стержня з ниткою 7, підставки для пластинки, відносно якої визначають
Установка РМ-07 складається з електронного блока вимірювання часу і кількості коливань 1, стержня 2, нитки 3, кульки 4, фотоелектричного датчика 5, шкали для вимінювання кута відхилення нитки 6, шкали для вимірювання кута відхилення стержня з ниткою 7, підставки для пластинки, відносно якої визначають

 N Якщо нитка, до кінця якої підвішена кулька 4 (рис. 9.2), і
N Якщо нитка, до кінця якої підвішена кулька 4 (рис. 9.2), і






 B З рівності (9.8) видно, що для визначення шляху S потрібно міряти довжину нитки, максимальні кути відхилення нитки першого і n-
B З рівності (9.8) видно, що для визначення шляху S потрібно міряти довжину нитки, максимальні кути відхилення нитки першого і n-




 Теоретичні відомості
Теоретичні відомості

 O характерний, так званий,
O характерний, так званий,

 O Визначимо кутову швидкість прецесії ω ΄. З
O Визначимо кутову швидкість прецесії ω ΄. З



 O обертання гіроскопа, І – момент інерції. Враховуючи
O обертання гіроскопа, І – момент інерції. Враховуючи












