Визначення швидкості польоту кулі за допомогою балістичного маятника

 

 

Мета роботи:

 

 

Обладнання:

визначити швидкість польоту кулі, використовуючи закони збереження. установка для визначення швидкості польоту

кулі.

 

 

O 2

 

1 4 3

5 6

 

 

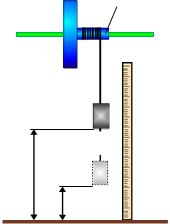
Рисунок 4.1

Дана установка (див. рис. 4.1) складається з масивного тіла 1, підвішеного на шарнірно закріпленому стержні 2, пружинного пістолета 3, з якого при пострілі вилітає куля 4. Біля тіла 1 знаходиться лінійка 5 з повзунком 6.

 

 

Теоретичні відомості

 

 

Після пострілу куля потрапляє в балістичний маятник і застрягає в ньому. Відбувається непружний удар і маятник відхиляється на кут α від вертикалі. При цьому тіло 1 відсуває повзунок на віддаль S.

Система куля - маятник перед ударом має момент імпульсу відносно точки О, який рівний моменту імпульсу кулі

L = mvl, (4.1)

 

де m - маса кулі, v - її швидкість, l - відстань від точки закріплення маятника до місця удару кулі в маятник. Після удару, коли куля застрягне в балістичному маятнику, останній починає обертатись навколо точки О, отже момент імпульсу системи

L = J w, (4.2)

 

де J - момент інерції маятника разом з кулею, що застрягла в ньому, ω - кутова швидкість. Із закону збереження моменту імпульсу

mvl = J w. (4.3)

 

l

w

Маятник відхиляється на кут α, при цьому центр мас піднімається на висоту h. Із закону збереження енергії маємо:

(M + m) gh = J 22, (4.4) де M — маса маятника, а M + m — маса системи маятник-куля. Розв'язавши спільно рівняння (4.3) і (4.4), одержимо:

 

v = ml 2 ghJ (M + m). (4.5) У зв'язку з тим, що маса тіла 1 набагато більша від

 

маси стержня 2, і розміри набагато менші, можна розглядами момент інерції системи, як момент інерції матеріальної точки:

J = (M + m) l 2, де m «М, тому

 

J = Ml 2. (4.6)

 

 

 

B h

 

C

Висоту h підняття центра мас знайдемо з таких міркувань: з рис.4.2 видно, що при піднятті центру мас на висоту h, повзунок переміщується на відстань S = АС.

Z

Умови досліду такі, що кут відхилення α дуже малий, тоді для нього, а тим більше для

S A a, виконується умова

2 2 2

Рисунок4.2 sin a = tg a»a. (4.7) З трикутника АВС h = S × tg a або з урахуванням (4.7)

 

a

h = S 2. (4.8)

 

a

При виконанні умови (4.7) можна вважати, що СА = ВА. Отже ZA = BA/2 = S/2. З трикутника ZОА

 

ZAS

2 = l = 2 l. (4.9) Тепер, з урахуванням (4.9)

S

2

h = 2 l. (4.10) Підставивши (4.6) і (4.10) в рівняння (4.5), одержимо

формулу для швидкості руху кулі

 

m

l

v = SMg. (4.11)

 

 

Порядок виконання роботи

 

 

1 Виміряти довжину l від точки закріплення О до середини тіла 1.

2. Виміряти масу кулі і масу маятника.

3. Зробити постріл і замітити, на яку віддаль S переміститься повзунок 6.

4. Дослід повторити декілька разів.

5. За формулою (4.11) визначити швидкість кулі. Обчислити відносну і абсолютну похибку.

 

 

Контрольні запитання

1. В чому полягає закон збереження моменту імпульсу? 2. Сформулювати закон збереження механічної енергії?

3. Як використовуються в даній роботі вище згадані закони?

4. Які удари називаються абсолютно пружними і абсолютно непружними?

5. Виведіть робочу формулу.

6. Виведіть формулу для обчислення похибок.

 

Лабораторнаробота№5

 

 

ВИЗНАЧЕННЯ МОМЕНТУ ІНЕРЦІЇ МАХОВОГО КОЛЕСА

 

 

Мета роботи:

 

 

Обладнання:

вивчення основних законів динаміки обертового руху.

махове колесо, вантажі, секундомір, штангенциркуль, лінійка.

 

 

Теоретичні відомості

 

Д С1

 

h1

 

ВС2

 

Момент інерції махового колеса визначають за допомогою приладу, зображеного на рис. 5.1. Прилад складається з махового колеса Д, насадженого на вал. Вал встановлено на підшипниках С1і С2. Махове колесо приводиться в обертовий рух вантажем масою m. На висоті h1 вантаж має потенціальну енергію

 

h2E п1 = mgh. (5.1)

 

Якщо дати можливість Рисунок5.1 вантажу падати, то потенціальна

енергія перейде в кінетичну енергію поступального руху вантажу E к = mv 2, кінетичну енергію

 

w

I

2

m 1

обертового, руху E к = 2 і на роботу по подоланню сили тертя A = Fh. Запишемо закон збереження енергії:

 

 

F =

1 2

,

w

m 1

mgh 1 = mv 2 + I 22 + Fh, (5.2)

 

де Fm — сила тертя. Рух вантажу рівноприскорений без початкової швидкості, тому прискорення а і швидкість v відповідно дорівнюють:

t

a = 2 h, (5.3)

 

h

v = at = 2 t 1, (5.4) де t — час опускання з висоти h 1. Кутову швидкість ω знайдемо з формули

rt

w = v = 2 h, (5.5)

 

 

де r — радіус валу В. Коли вантаж дійде до нижньої точки, махове колесо по інерції буде продовжувати обертатися і вантаж підніметься на висоту h 2< h 1. На висоті h2 система буде мати запас потенціальної енергії

 

E п2 = mgh 2. (5.6)

 

Так як h 2< h 1то Е п2< E п1. Зменшення потенціальної енергії дорівнює роботі сил тертя:

 

(

1 2 m 1 2

mgh - mgh = Fh + h). (5.7)

 

Звідси сила тертя

 

mg (h - h) mh + h

 

(5.8)

 

1 2

де h 1— висота, з якої падає вантаж; h 2— висота, на яку піднімається вантаж, досягнувши самої нижньої точки. Підставляючи в рівняння (5.2), значення v, ω і Fm і

 

розв'язавши його відносно І, одержимо формулу для знаходження моменту інерції махового колеса:

 

 

æ ö

h

ç ÷

è ø

1 1 2

I = mr 2 ç gt 2 h (h + h) - 1 ÷. (5.9)

 

 

Порядок виконання роботи

 

 

1. Штангенциркулем виміряти радіус вала В.

2. Накрутити на вал нитку і підняти вантаж до висоти h1.

3. Секундоміром виміряти час падіння вантажу з висоти h1.

4. Виміряти висоту h2, на яку піднімається вантаж після досягнення крайньої нижньої точки.

5. Дослід повторити п'ять разів. Результати записати в таблицю і за допомогою формули (5.9) визначити момент інерції махового колеса, а за допомогою формули (5.8) силу тертя.

6. Похибки обчислити згідно методичних вказівок

 

 

Контрольні запитання

 

 

1. Що називається моментом сили? Одиниці його вимірювання?

2. Що називається моментом інерції? Фізичний зміст моменту інерції.

3. Сформулювати і пояснити теорему Штейнера.

4. Сформулювати основний закон динаміки обертального руху.

5. Який закон динаміки покладено в основу робочої формули?

 

 



dL

Лабораторнаробота№6