
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие вектора и линейные операции над векторами.
Вектором называется произвольный направленный отрезок. В дальнейшем, для обозначения вектора, будем пользоваться символом
Начало вектора называется точкой его приложения. Длина вектора обозначается следующим образом Вектор называется нулевым, если начало и конец его совпадают. Нулевой вектор не имеет определённого направления и имеет длину равную нулю. Векторы называются коллинеарными, если они лежат на одной прямой, либо на параллельных прямых. Два вектора называются равными, если они коллинеарны, имеют одинаковую длину и одинаковое направление. Все нулевые векторы считаются равными. Суммой двух векторов
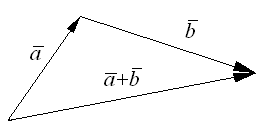
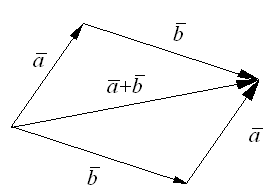
Данное правило сложения двух векторов называется правилом треугольника. Очевидно, что этот же вектор
Это правило сложения векторов называется правилом параллелограмма. Правило сложения векторов обладает следующими свойствами: 1. 2. 3. Существует нулевой вектор 4. Для любого вектора
Доказательство свойств 1 и 2 для неколлинеарных векторов проводится непосредственно построением.
Для коллинеарных векторов свойства 1, 2 доказать самостоятельно. Свойство 3 очевидно. Свойство 4. Очевидно, так как для любого вектора Разностью векторов Разность векторов Теорема 3.1. Для любых векторов Доказательство. Рассмотрим вектор Докажем единственность разности векторов
Следовательно если
Замечание. Правило параллелограмма сложения неколлинеарных векторов
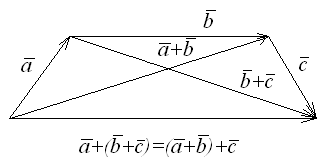
Свойства 1 -4 позволяют распространить правило сложения на сумму любого конечного числа векторов. Сумма любого конечного числа векторов может быть построена с помощью следующего правила: если приложить вектор Естественно назвать это правило сложения векторов правилом замыкания ломаной до многоугольника.
Произведением Замечание. В случае, когда Операция умножения вектора на число обладает следующими свойствами: 5. 6. 7. Свойства 5 – 7 доказываются одинаково. Приведём доказательство свойства 5 для неколлинеарных векторов и при условии
Приложим векторы
С другой стороны, из подобия треугольников
Из равенств (2) и (3) следует, что Доказательство свойства 5 для случая коллинеарных векторов и для случая
|
|||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 99; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.224.197 (0.013 с.) |
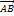 , где
, где 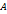 – начало, а
– начало, а 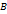 конец данного направленного отрезка, либо одной латинской буквой, снабженной чертой, либо просто жирной латинской буквой, например
конец данного направленного отрезка, либо одной латинской буквой, снабженной чертой, либо просто жирной латинской буквой, например 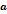 или
или  На чертеже будем изображать вектор стрелкой, причём букву обозначающую этот вектор будем ставить у его конца.
На чертеже будем изображать вектор стрелкой, причём букву обозначающую этот вектор будем ставить у его конца.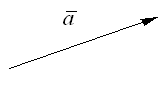
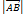 или
или 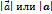 .
.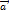 и
и  называется вектор, идущий из начала вектора
называется вектор, идущий из начала вектора  при условии, что вектор
при условии, что вектор 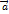 .
.
 для неколлинеарных векторов
для неколлинеарных векторов 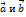 может быть получен, как диагональ параллелограмма, построенного на векторах
может быть получен, как диагональ параллелограмма, построенного на векторах 

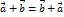 (Коммутативность сложения)
(Коммутативность сложения)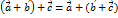 (Ассоциативность сложения)
(Ассоциативность сложения) , такой что
, такой что 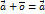 для любого вектора
для любого вектора 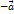 , такой, что
, такой, что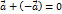 .
.
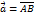 существует вектор
существует вектор 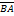 , такой что
, такой что  . Т.е.
. Т.е. 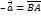 .
. , что
, что 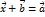 .
.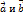 обозначается
обозначается 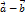 .
.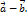
 . Тогда
. Тогда 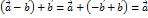 . Следовательно существует разность
. Следовательно существует разность  - разность векторов
- разность векторов 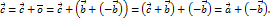
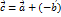 . Единственность доказана.
. Единственность доказана.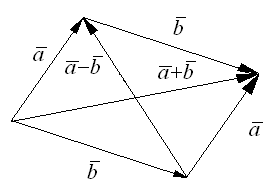
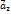 к концу вектора
к концу вектора 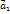 , вектор
, вектор 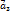 к концу вектора
к концу вектора  к концу вектора
к концу вектора  , то сумма
, то сумма 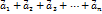 представляет собой вектор, идущий из начала вектора
представляет собой вектор, идущий из начала вектора 
 вектора
вектора  на число
на число 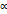 называется вектор
называется вектор  , коллинеарный вектору
, коллинеарный вектору  и направление, совпадающее с направлением вектора
и направление, совпадающее с направлением вектора  и противоположное направлению
и противоположное направлению 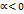 .
.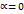 , или
, или 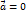 произведение
произведение 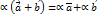 ;
;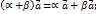
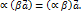
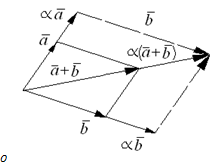
 . Построим вектор
. Построим вектор 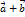 , как диагональ параллелограмма, построенного на векторах
, как диагональ параллелограмма, построенного на векторах  - конец вектора
- конец вектора 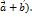 Т.к.
Т.к. 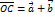 и
и 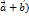 имеют одинаковые направления. Пусть
имеют одинаковые направления. Пусть 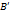 - точка пересечения прямой
- точка пересечения прямой 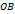 и прямой, проходящей через точку
и прямой, проходящей через точку  - точка пересечения прямой
- точка пересечения прямой  и прямой, проходящей через точку
и прямой, проходящей через точку 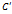 параллельно вектору
параллельно вектору 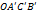 является параллелограммом. Следовательно
является параллелограммом. Следовательно
 ,
, 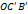 и треугольников
и треугольников 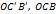 следует, что
следует, что
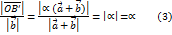
 ,
, 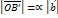 . Т.к.
. Т.к. 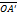 и
и 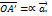 Аналогично
Аналогично  . Учитывая полученные выражения
. Учитывая полученные выражения  , найдем
, найдем 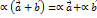 .
.


