
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Системы с верхней трапециевидной матрицей.
Рассмотрим систему линейных алгебраических уравнений Возможны следующие четыре случая. Случай 1. Пусть матрица
В случае 1 система (1) имеет вид
При этом расширенная матрица системы (2) имеет вид Легко заметить, что Найти решение системы (2) не представляет труда: решая последовательно уравнения системы снизу вверх, мы каждый раз будем иметь дело с уравнением, содержащим только одно неизвестное. Заметим, что в случае 1 система (2), а стало быть и система (1) имеет единственное решение. Случай 2. Пусть матрица
В случае 2 система (1) имеет вид
А расширенная матрица Как и в случае (1), Назовём неизвестные Перенося в уравнениях системы (3) все слагаемые, содержащие свободные неизвестные в правую часть, получим
Решая последовательно уравнения системы (4) снизу вверх, мы получим выражения главных неизвестных Придавая свободным неизвестным произвольные числовые значения Очевидно, что упорядоченный набор Так как свободным неизвестным можно придать бесконечное множество значений, то и система (3) имеет бесконечное множество решений. Следовательно, система (1), в случае Случай 3. Пусть матрица
Тогда система (1) имеет следующий вид
Докажем, что система (5) совместна тогда и только тогда, когда Доказательство. Пусть система (5) совместна. Тогда существуют такие значения неизвестных
Система (6) называется укороченной системой. Очевидно, что, при выполнении равенств
Основная матрица системы (6) имеет вид, рассмотренный в случае 2. Следовательно, система (6) имеет бесконечное множество решений, а стало быть, совместна.
Заметим, что в случае 3, при выполнении равенств системы (5) является верхней трапециевидной матрицей, при этом
Таким образом, в случае Случай 4. Пусть верхняя трапециевидная матрица
Тогда система (1) имеет вид
Из чего следует, что система (7) совместна тогда и только тогда, когда все Заметим, что в случаях 3 и 4, равенство Из проведённых выше рассуждений следует, что система линейных алгебраических уравнений с верхней трапециевидной матрицей совместна тогда и только тогда, когда ранг основной матрицы Системы общего вида Теорема Кронекера-Капелли. Рассмотрим систему где Теорема 5.1.(Кронекера-Капелли). Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг основной матрицы равен рангу расширенной матрицы. Доказательство. Пусть эквивалентную системе (1). В силу теоремы 6.3 гл.1 Заметим, что матрица неизвестных Система (2) является системой с верхней трапециевидной матрицей. В силу результатов §4 главы 2, система (2) совместна тогда и только тогда, когда
Заметим, что при выполнении равенства (4), матрица Из равенств (3), (4)и (5) следует, что система (1) совместна тогда и только тогда, когда Метод Гаусса исследования и решения системы. Метод Гаусса исследования и решения системы уравнений состоит в приведении её к системе с верхней трапециевидной матрицей, и последующим исследованием и решением получившейся системы.
Согласно теореме 3.1 §3 главы 1, основная матрица Из проведённых выше рассуждений следует справедливость следующей теоремы. Теорема 5.2. (О структуре множества решений) Любая система линейных алгебраических уравнений c основной матрицей Пример 1. Исследовать и решить систему
Решение. Элементарными преобразованиями строк расширенной матрицы приведём матрицу системы к верхней трапециевидной форме
Система с последней расширенной матрицей несовместна. Пример 2. Исследовать и решить систему
Решение. Элементарными преобразованиями строк расширенной матрицы приведём матрицу системы к верхней трапециевидной форме.
Пример. Исследовать и решить систему
Построить её общее решение, указать какое-нибудь частное решение. Элементарными преобразованиями приведём расширенную матрицу системы к верхней трапециевидной форме
Как видим, свободными неизвестными будут
последовательно снизу вверх.
Итак, общее решение системы имеет вид Частное решение системы получится, если в её общем решении задать значения свободных неизвестных, например, положить их равными
|
||||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 62; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.25.32 (0.029 с.) |
 с верхней трапециевидной матрицей
с верхней трапециевидной матрицей 
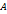 имеет вид
имеет вид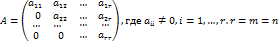
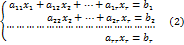
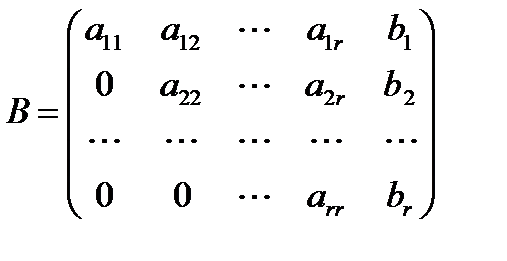 .
.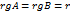 .
.

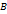 - вид
- вид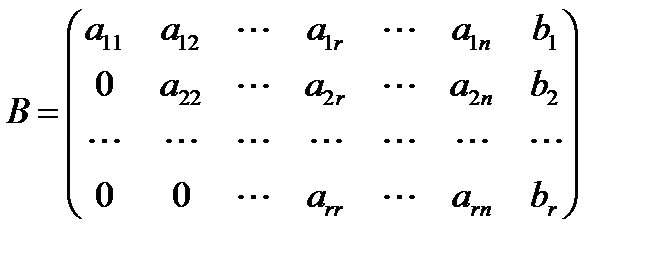 .
.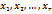 – главными неизвестными, а
– главными неизвестными, а  – свободными.
– свободными.
 , вычислим соответствующие значения главных неизвестных. Пусть эти значения
, вычислим соответствующие значения главных неизвестных. Пусть эти значения  .
. является решением системы (3). Это решение называется частным решением.
является решением системы (3). Это решение называется частным решением.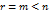 имеет бесконечное множество решений.
имеет бесконечное множество решений.

 .
.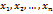 , при которых все уравнения системы превращаются в тождества. Следовательно
, при которых все уравнения системы превращаются в тождества. Следовательно 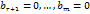 . Пусть теперь выполнены равенства
. Пусть теперь выполнены равенства 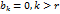 . Тогда система (5) имеет вид
. Тогда система (5) имеет вид
 системы (5) и (6) эквивалентны.
системы (5) и (6) эквивалентны.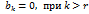 , расширенная матрица
, расширенная матрица 
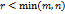 , если среди коэффициентов
, если среди коэффициентов 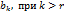 хотя бы один не равен нулю, то система (5) несовместна. Если же все
хотя бы один не равен нулю, то система (5) несовместна. Если же все 
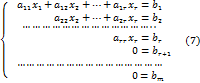
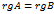
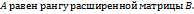 При этом система либо имеет единственное решение (
При этом система либо имеет единственное решение (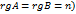 , либо имеет бесконечное множество решений (
, либо имеет бесконечное множество решений ( , либо не имеет ни одного решения (
, либо не имеет ни одного решения (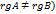
 , (1)
, (1)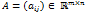 ,
,  ,
,  .
. - верхней трапециевидной формы. Применяя эти преобразования к расширенной матрице
- верхней трапециевидной формы. Применяя эти преобразования к расширенной матрице 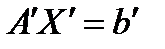 (2)
(2)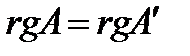 . (3)
. (3) может отличаться от матрицы
может отличаться от матрицы  только нумерацией неизвестных.
только нумерацией неизвестных.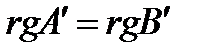 . (4)
. (4)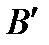 является матрицей верхней трапециевидной формы, полученной из матрицы
является матрицей верхней трапециевидной формы, полученной из матрицы 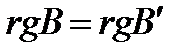 . (5)
. (5) .
. и числом неизвестных
и числом неизвестных  либо совместна и имеет единственное решение (
либо совместна и имеет единственное решение (


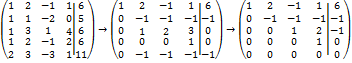
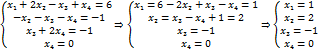


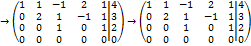
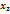 и
и  . Выразим через них главные неизвестные, решая уравнения системы
. Выразим через них главные неизвестные, решая уравнения системы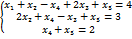

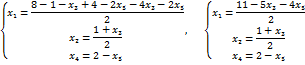
 .
. . Тогда
. Тогда  . Следовательно
. Следовательно  - частное решение.
- частное решение.


