
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Элементы интегрального исчисленияСтр 1 из 25Следующая ⇒
Первообразная функции. Неопределенный интеграл Если основной задачей дифференциального исчисления было отыскание производной данной функции, то основной задачей интегрального исчисления является отыскание функции по ее производной. Функция В качестве первообразной для функции Совокупность всех первообразных для функции Правила интегрирования: 1) 2)
Таблица неопределенных интегралов:
Методы интегрирования: 1) метод замены переменных
Пример:
2) метод интегрирования по частям: Пример: Определенный интеграл Рассмотрим задачу о вычислении площади криволинейной трапеции. Криволинейной трапецией называется плоская фигура, ограниченная осью Ox, графиком непрерывной функции
Разделим основание трапеции Обозначим В общем случае предел, к которому стремится интегральная сумма Для того чтобы вычислить определенный интеграл от заданной функции
Пример:
Глава 3 Дифференциальные уравнения
Дифференциальным уравнением называется уравнение, содержащее в общем случае аргумент, функцию и ее производные или дифференциалы различных порядков
Если функция зависит от одной переменной, то дифференциальное уравнение называется обыкновенным. Порядком дифференциального уравнения называется порядок старшей производной, входящего в него. Пример: обыкновенное дифференциальное уравнение 1-го порядка Решением дифференциального уравнения называется функция, подстановка которой в дифференциальное уравнение обращает его в тождество. Общим решением дифференциального уравнения является множество решений, содержащее произвольную постоянную C: Решение дифференциального уравнения, не содержащее произвольной постоянной, называется частным. Для его нахождения надо знать так называемые начальные условия, то есть пару значений Пример: дифференциальное уравнение Дифференциальное уравнение 1-го порядка называется уравнением с разделяющимися переменными, если его можно представить в виде: Запишем дифференциальное уравнение с разделяющимися переменными в виде Пример: решим дифференциальное уравнение
Глава 4
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 68; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.204.8 (0.007 с.) |
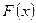 называется первообразной для функции
называется первообразной для функции 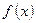 , если выполняется тождество
, если выполняется тождество  . Пример:
. Пример: 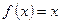 ,
, 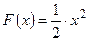 ,
, 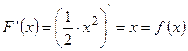 .
.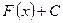 , С –произвольная постоянная, так как
, С –произвольная постоянная, так как 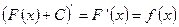 .
. . Чтобы найти неопределенный интеграл от заданной функции
. Чтобы найти неопределенный интеграл от заданной функции 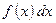 , найти первообразную
, найти первообразную  .
.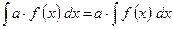 ;
; .
.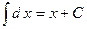
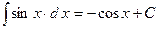
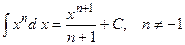
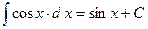
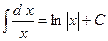
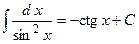
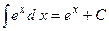
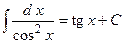

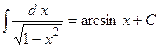
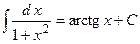
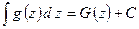 ,
, 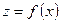 .
.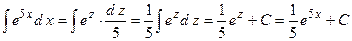 ,
,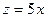 ,
, 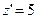 ,
, 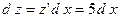 ,
,  .
.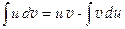 .
.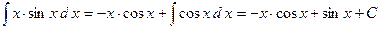 .
.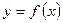 и двумя вертикальными прямыми
и двумя вертикальными прямыми 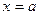 и
и 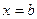 (рис. 2.1).
(рис. 2.1).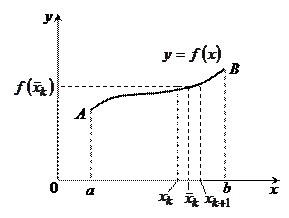
 на n частичных интервалов
на n частичных интервалов 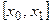 ,
, 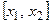 ,...,
,..., 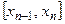 , считая что
, считая что  . Проведем через эти точки прямые, параллельные оси Oy, тогда фигура aABb разделится на n элементарных криволинейных трапеций.
. Проведем через эти точки прямые, параллельные оси Oy, тогда фигура aABb разделится на n элементарных криволинейных трапеций.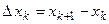 ,
,  . Возьмем некоторую точку
. Возьмем некоторую точку 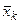 из малого интервала
из малого интервала  . Вычислим площадь элементарного прямоугольника с основанием
. Вычислим площадь элементарного прямоугольника с основанием 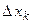 и высотой
и высотой  :
: 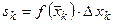 . Сумма площадей всех прямоугольников является приближением для площади криволинейной трапеции:
. Сумма площадей всех прямоугольников является приближением для площади криволинейной трапеции: 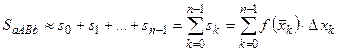 - интегральная сумма. Причем чем меньше
- интегральная сумма. Причем чем меньше  .
.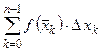 при
при  , называется определенным интегралом и обозначается
, называется определенным интегралом и обозначается 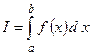 .
.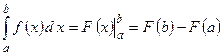 . (формула Ньютона-Лейбница)
. (формула Ньютона-Лейбница)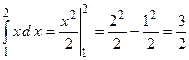 .
. .
. .
. .
. . Подставляя начальные условия в общее решение, можно определить постоянную интегрирования C. Возвращаем ее значение в общее решение, в результате получаем частное решение дифференциального уравнения.
. Подставляя начальные условия в общее решение, можно определить постоянную интегрирования C. Возвращаем ее значение в общее решение, в результате получаем частное решение дифференциального уравнения. имеет общее решение
имеет общее решение 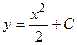 . Пусть начальное условие задано в виде:
. Пусть начальное условие задано в виде: 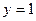 при
при 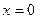 . Тогда из общего решения найдем постоянную C:
. Тогда из общего решения найдем постоянную C:  ,
,  . Откуда
. Откуда 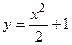 - частное решение дифференциального уравнения.
- частное решение дифференциального уравнения.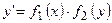 . Правая часть этого уравнения есть произведение двух функций, каждая из которых зависит только от одной переменной. Пример:
. Правая часть этого уравнения есть произведение двух функций, каждая из которых зависит только от одной переменной. Пример:  ,
,  ,
, 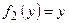 .
.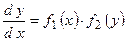 . Отсюда получим
. Отсюда получим  . Найдем интеграл
. Найдем интеграл  . Решая его, получим выражение
. Решая его, получим выражение  , из которого выражаем общее решение
, из которого выражаем общее решение 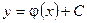 .
.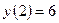 . Для этого представим уравнение в виде
. Для этого представим уравнение в виде  и далее
и далее  ,
, 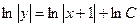 ,
, 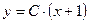 - общее решение. Воспользуемся начальными условиями, чтобы найти постоянную интегрирования:
- общее решение. Воспользуемся начальными условиями, чтобы найти постоянную интегрирования:  ,
, 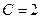 . Тогда
. Тогда  - частное решение.
- частное решение.


