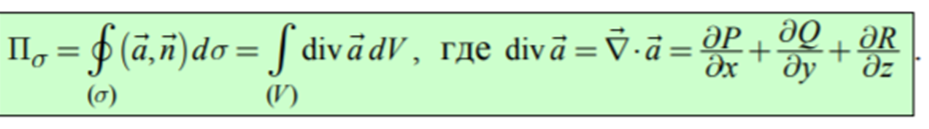Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Производная поля по направлению
(Определение) Производной поля f (M) в точке M в направлении вектора l называют величину
Свойства производной по направлению
3.3. Градиент скалярного поля: его свойства, инвариантное определение.
инвариантное определение градиента Градиент скалярного поля f (M) в точке M0 есть вектор, который а) по величине равен наибольшей скорости возрастания поля f (M) в точке M0, б) направлен по нормали к поверхности уровня поля f (M), проходящей через точку M0, в сторону наибольшего возрастания поля
Векторное поле 4.1 Векторное поле – это область пространства, в каждой точке M которой задан вектор Примеры векторных полей: 1) Пусть на материальную точку в области D действует сила 2) Пусть в области D происходит течение жидкости и в каждой точке M задан вектор 3) Поместим заряд + q в начало координат. Тогда сила, с которой этот заряд действует на единичный положительный заряд, помещенный в точку M, определяется по закону Кулона:
Векторные линии: (характеристика векторного поля) Векторной линией векторного поля называют линию, в каждой точке которой касательный вектор коллинеарен вектору поля. Выведем уравнения векторных линий для поля
Пусть уравнения векторной линии x=x(t), y=y(t), z=z(t),(t - параметр). Касательным вектором этой линии является вектор
По определению векторной линии ее касательный вектор
Мы получили систему дифференциальных уравнений для отыскания векторных линий поля
Поток поля через ориентированную поверхность: различные формы записи, способы Вычисления. Ориентированная поверхность – это поверхность, в каждой точке которой выбрано направление нормали с помощью единичного вектора n(М), где n(M) является непрерывной вектор-функцией точки М. Поток векторного поля Потоком векторного поля a через ориентировочную поверхность ( Записи: 1) 2) 3) Вычисление: 1) По формуле 2) Методом проектирования на 3 плоскости
а) в подынтегральной функции заменить x его значением x=x(y,z) на поверхности б) учесть, что d в) вычислить получившийся двойной интеграл по проекции Другие вычисляются аналогично 3) Методом проектирования на одну плоскость Воспользуемся параметрическим уравнением поверхности Нормальный вектор поверхности: Элемент площади
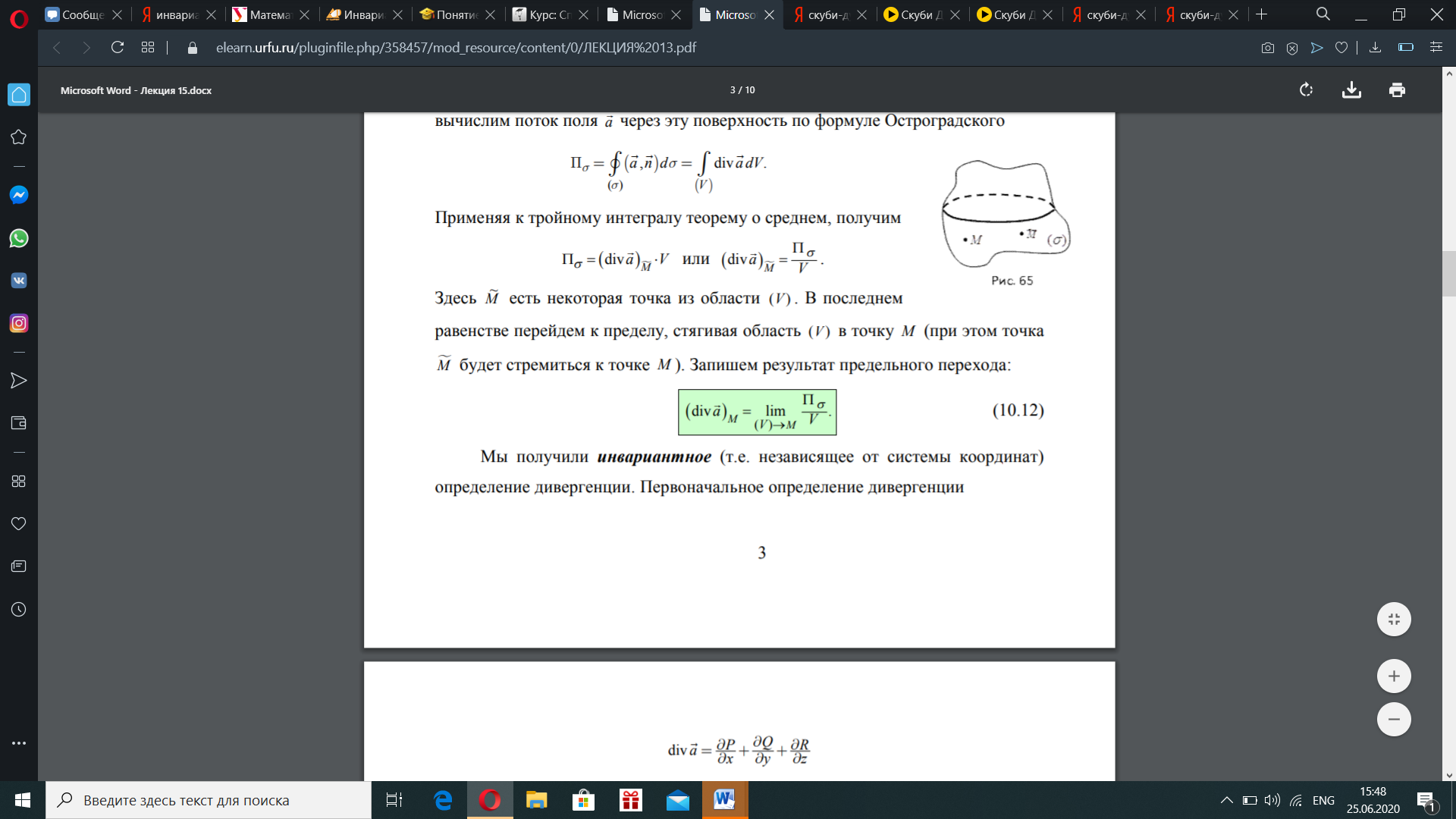
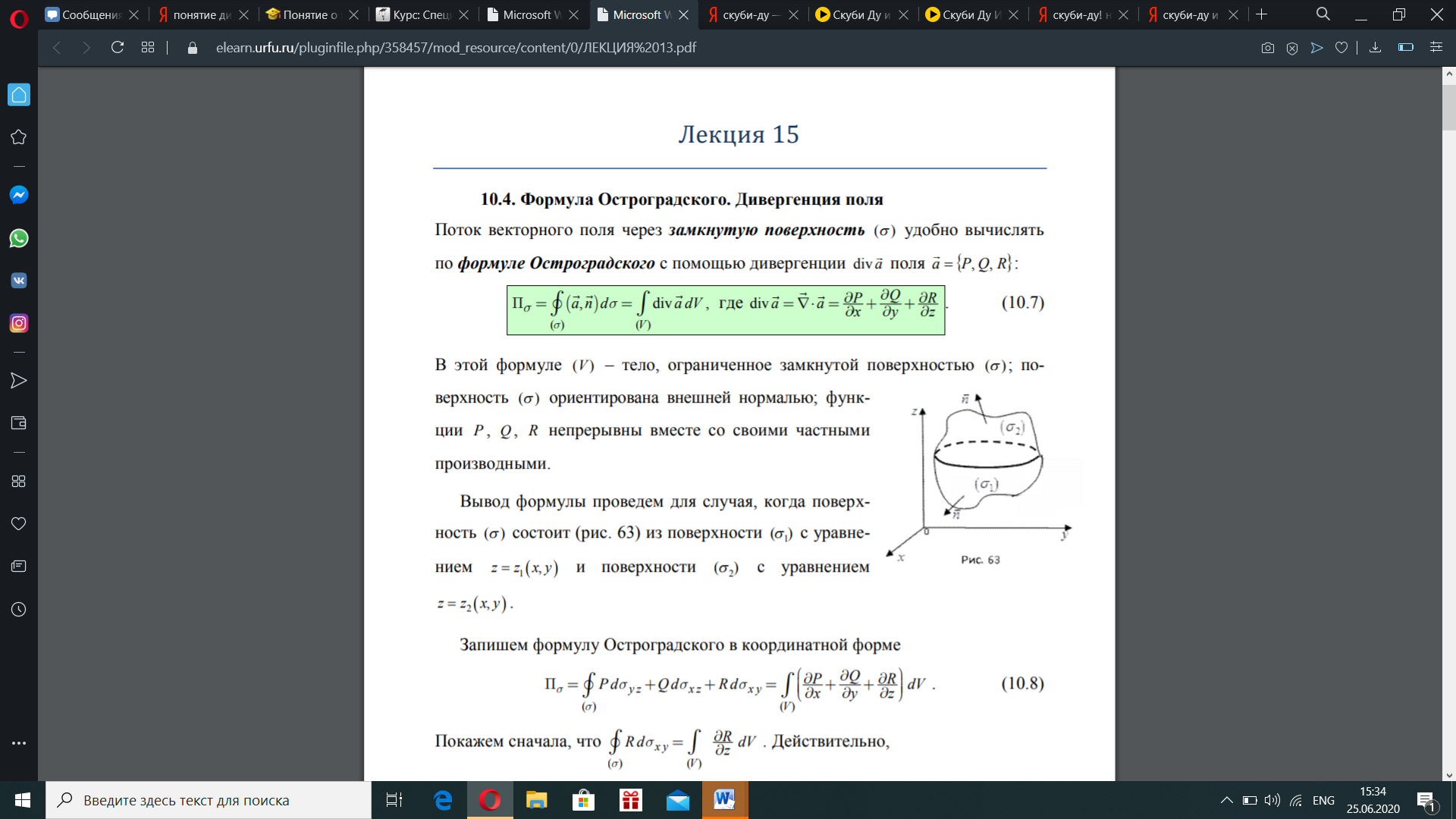
4.3 . Формула Остроградского и понятие дивергенции. Инвариантное определение дивергенции, ее свойства. Формула Остроградского Поток векторного поля через замкнутую поверхность (s) удобно вычислять по формуле Остроградского с помощью дивергенции div a поля a = {P, Q, R}
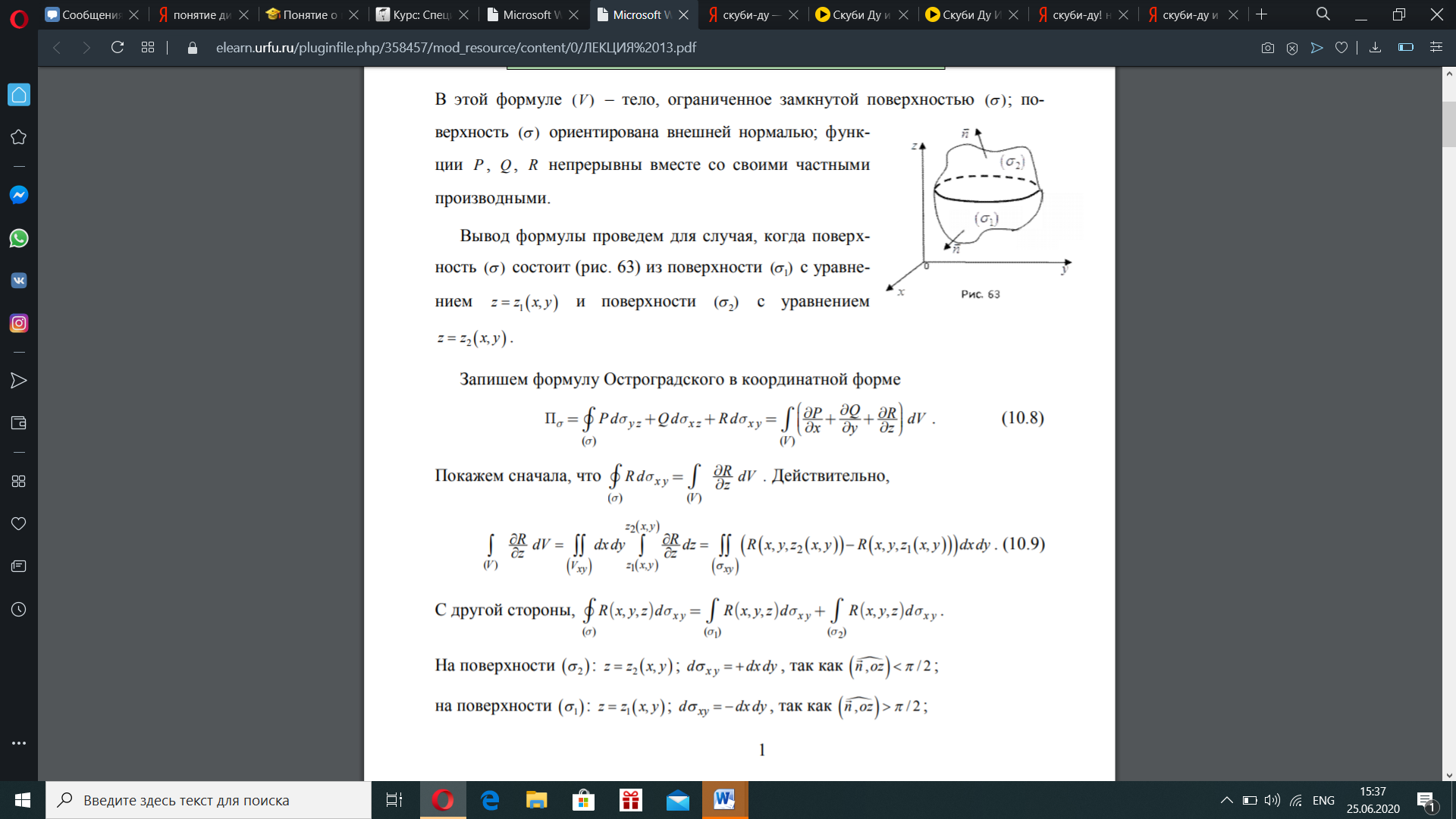
В этой формуле () V – тело, ограниченное замкнутой поверхностью (s); поверхность (s) ориентирована внешней нормалью; функции P, Q, R непрерывны вместе со своими частными производными. Запишем формулу Остроградского в координатной форме
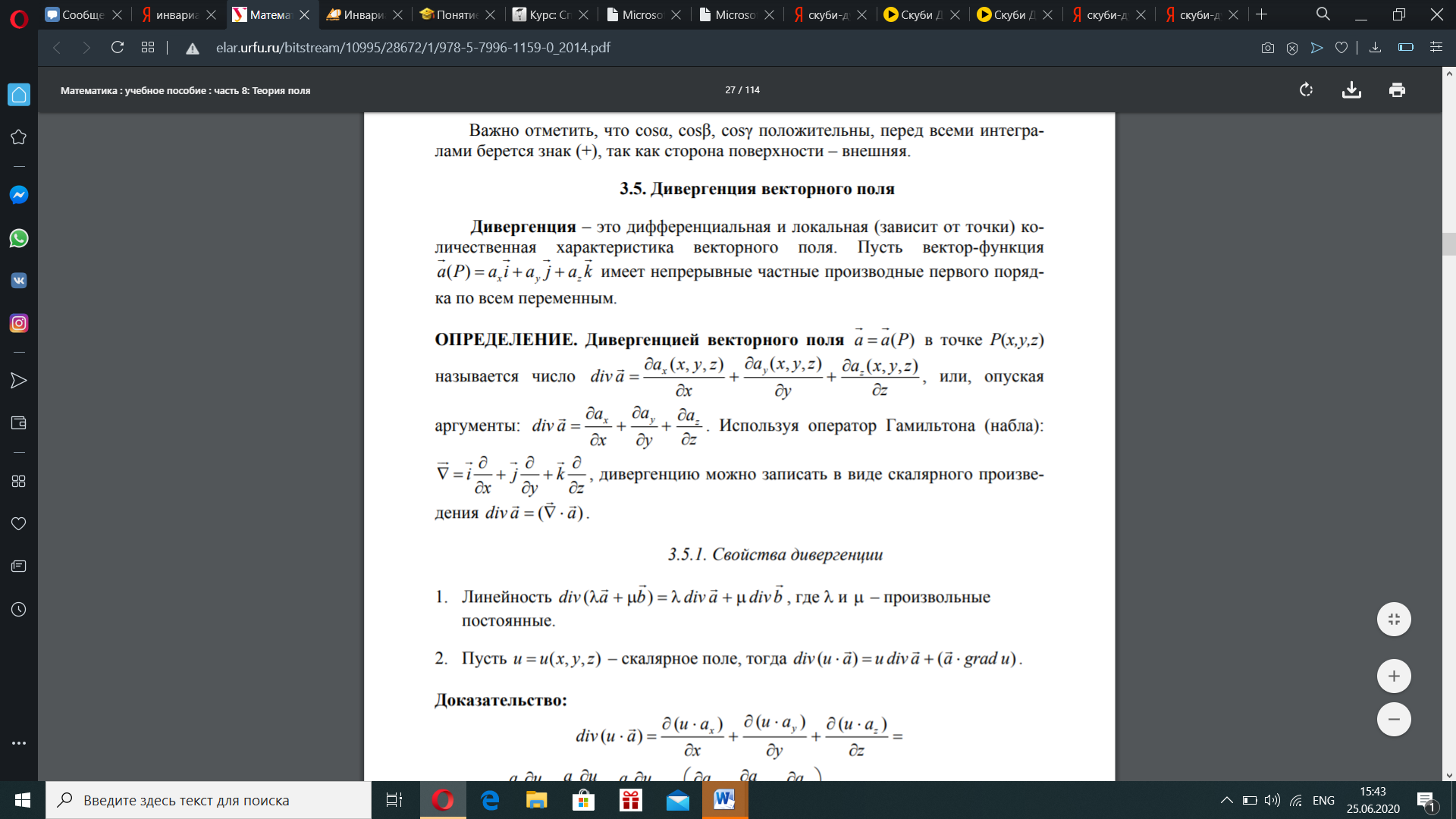
Понятие дивергенции Дивергенция – это дифференциальная и локальная (зависит от точки) количественная характеристика векторного поля. Пусть вектор-функция
Мы получили инвариантное (т.е. независящее от системы координат) определение дивергенции.
|
||||||
|
Последнее изменение этой страницы: 2021-06-14; просмотров: 118; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.209.8 (0.016 с.) |

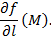 2). Поле f (M) в точке M в направлении l возрастает тогда и только тогда, когда
2). Поле f (M) в точке M в направлении l возрастает тогда и только тогда, когда
 3). Поле f (M) в точке M в направлении l убывает тогда и только тогда, когда
3). Поле f (M) в точке M в направлении l убывает тогда и только тогда, когда
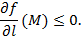 4). Если вектор l || ox, то
4). Если вектор l || ox, то 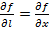 ; если вектор
; если вектор 

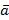 (M).
(M).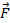 (M). Тогда в области D определено векторное поле
(M). Тогда в области D определено векторное поле 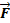 ((M).
((M).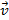 (M) скорости частицы жидкости. Тогда в области D определено векторное поле скоростей жидкости
(M) скорости частицы жидкости. Тогда в области D определено векторное поле скоростей жидкости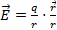 , где r r – вектор, идущий из начала координат в точку M (радиус-вектор точки M), r – его длина. Имеем векторное поле напряженностей
, где r r – вектор, идущий из начала координат в точку M (радиус-вектор точки M), r – его длина. Имеем векторное поле напряженностей 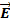 (M), создаваемое зарядом q.
(M), создаваемое зарядом q.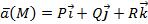
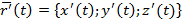 и вектор
и вектор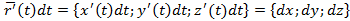 .
. и вектор поля
и вектор поля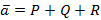 коллинеарны. Поэтому координаты этих векторов пропорциональны, т. е.
коллинеарны. Поэтому координаты этих векторов пропорциональны, т. е.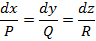
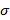 ) с единичным нормальным вектором n называют величину:
) с единичным нормальным вектором n называют величину: 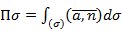
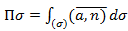 – векторная форма записи
– векторная форма записи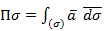 - векторная форма записи
- векторная форма записи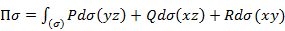 – координатная форма записи
– координатная форма записи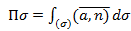
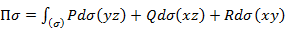 =
= 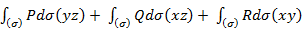

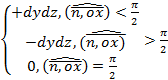
 :
: 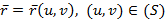
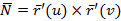
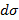 :
: 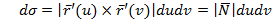
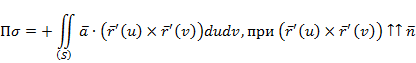
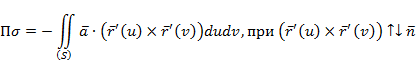
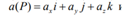 имеет непрерывные частные производные первого порядка по всем переменным
имеет непрерывные частные производные первого порядка по всем переменным