
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Признаки сходимости знакоположительных рядов.Стр 1 из 6Следующая ⇒
Ряды 1.1. Числовой ряд, его сходимость, сумма. Признаки сходимости знакоположительных рядов. Знакочередующийся ряд, признак Лейбница. Знакопеременные ряды, абсолютная и условная сходимости. Комплексные числовые ряды. 1.2. Степенные ряды и их свойства. Ряды Тейлора и их применение к вычислению значений функции, к вычислению определенных интегралов, к решению дифференциальных уравнений. 1.3. Разложение периодической функции в тригонометрический ряд Фурье. Ряд Фурье для четной и нечетной функции. Разложение функции, заданной на отрезке в ряд Фурье. Ряд Фурье в комплексной форме. Спектральные характеристики периодической функции. 2. Интегралы по фигуре 2.1. Понятие фигуры, её диаметра, меры. Вычисление массы фигуры. Понятие интеграла по фигуре, его свойства и приложения. 2.2. Конкретные виды интеграла по фигуре: криволинейный, двойной, тройной, поверхностный. 2.3. Вычисление криволинейного интеграла 1-го рода. 2.4. Вычисление двойного и тройного интеграла в прямоугольной и криволинейной системах координат. 2.5. Вычисление поверхностного интеграла 1-го рода. Скалярное поле 3.1. Скалярное поле. Поверхности (линии) уровня. 3.2. Производная поля по направлению. 3.3. Градиент скалярного поля: его свойства, инвариантное определение. Векторное поле 4.1. Примеры векторных полей. Векторные линии. 4.2. Поток поля через ориентированную поверхность: различные формы записи, способы вычисления. 4.3. Формула Остроградского и понятие дивергенции. Инвариантное определение дивергенции, ее свойства. 4.4. Вычисление работы в силовом поле. Линейный интеграл поля и циркуляция: свойства, различные формы записи, способы вычисления. 4.5. Формула Стокса. Понятие ротора: его физический смысл. 4.6. Условие независимости линейного интеграла поля от формы пути интегрирования. 4.7. Потенциальное поле, отыскание скалярного потенциала. Соленоидальное поле, гармонические поля. 4.8. Повторные операции теории поля. Оператор Гамильтона Ñ. Запись основных характеристик скалярного и векторного поля с помощью Ñ. Правила действия с Ñ
1.Ряды 1.1 Числовой ряд, его сходимость, сумма Числовой ряд – это сумма бесконечного числа членов числовой последовательности вида
где числа а1, а2, а3, …. an – называются членами ряда, член аn – общим или n-ым членом ряда. Сумма конечного числа к первых членов ряда – называется к - ой частичной суммой ряда – S n Если существует конечный предел последовательности частичной суммы ряда, то ряд называется сходящимся, а число S – называется суммой ряда
Если же предел последовательности частичных сумм равен ∞ или не существует, то ряд называется расходящимся.
Знакочередующийся ряд Знакочередующийся ряд — это ряд вида
Теорема Лейбница (признак Лейбница) Знакочередующийся ряд сходится, если: 1) последовательность абсолютных величин членов ряда монотонно убывает: 2) общий член ряда стремится к нулю, то есть
Знакопеременный ряд
Ряд называется знакопеременным, если среди его членов имеются как положительные так и отрицательные члены. Знакочередующиеся ряды являются частным случаем знакопеременных рядов.
Теорема (достаточный признак сходимости знакопеременного ряда)
Пусть дан знакопеременный ряд
Если сходится ряд составленный из абсолютных величин данного ряда
то сходится и сам знакопеременный ряд. Комплексные числовые ряды Числовым рядом с комплексными членами называется ряд
Где Сn=an + ibn, a и b – действительные числа.
1.2 Степенные ряды Степенным рядом называется функциональный ряд вида
или вида
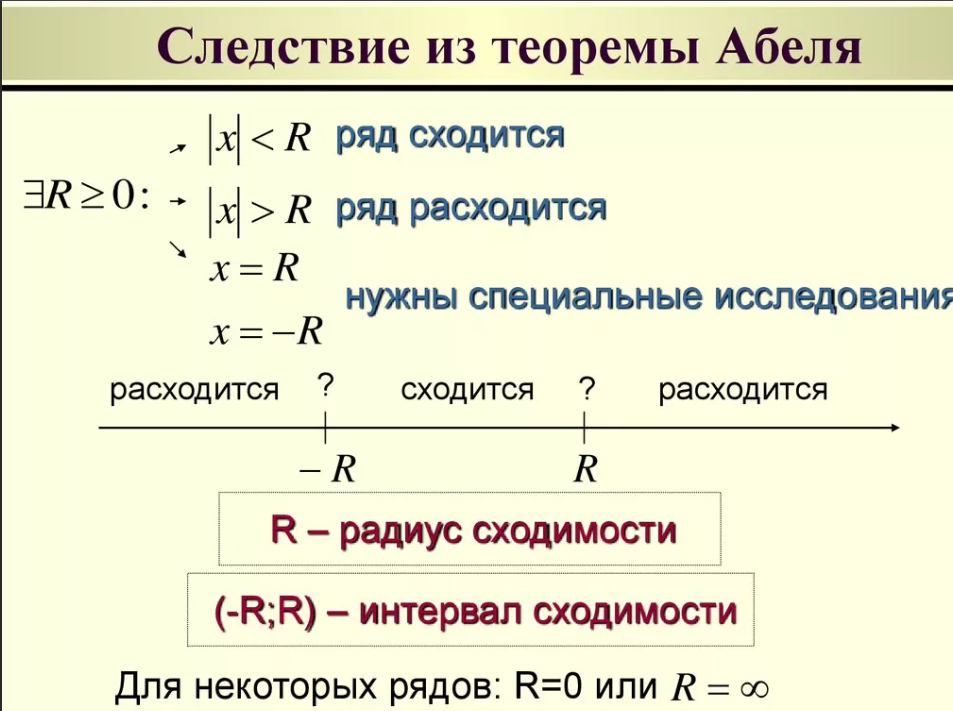
где x0, a0, a1, a2,... — действительные числа. Областью сходимости степенного ряда всегда является некоторый интервал, который, в частности, может вырождаться в точку.
Теорема Абеля 1) Если степенной ряд сходится при 2) Если ряд расходится при некотором значении х0', то он расходится при всяком x, для которого
Свойства степенных рядов Пусть дан некоторый степенной ряд (1) 1) Сумма степенного ряда (1) есть функция непрерывная во всех внутренних точках интервалов сходимости ряда 2) Степенной ряд (1) можно почленно интегрировать если пределы интегрирования являются внутренними точками интервала сходимости ряда.
3) Если степенной ряд (1) почленно проинтегрировать на отрезке (-R; R) [0;х] |x|<R, то полученный степенной ряд будет иметь тот же радиус сходимости R, что и степенной ряд (1). 4) Степенной ряд (1) внутри его интервала сходимости можно почленно дифференцировать сколь угодно раз. Получаем, что степенные ряды имеют тот же радиус сходимости R, что и ряд (1). Дифференциальных уравнений. Пусть f (x) определена в некоторой окрестности точки х0 и имеет в этой точке производные всех порядков, тогда степенной ряд Называется рядом Тейлора функции f(x) в точке x0 В случае x0 = 0 ряд называется рядом Маклорена в точке x0=0
Значений функции
Разложение периодической функции в тригонометрический ряд Фурье. Ряд Фурье для четной и нечетной функции. Разложение функции, заданной на отрезке в ряд Фурье. Ряд Фурье в комплексной форме. Спектральные характеристики периодической функции. Стандартная (=обычная) запись через сумму sinx и cosx
f(x)=ao+ a1cosx+a2cos2x+a3cos3x+...+b1sinx+b2sin2x+b3sin3x+..., где ao, a1,a2,...,b1,b2,.. - действительные константы, т.е.
Ряд Фурье для четной и нечетной функции
Интегралы по фигуре Вычисление массы фигуры
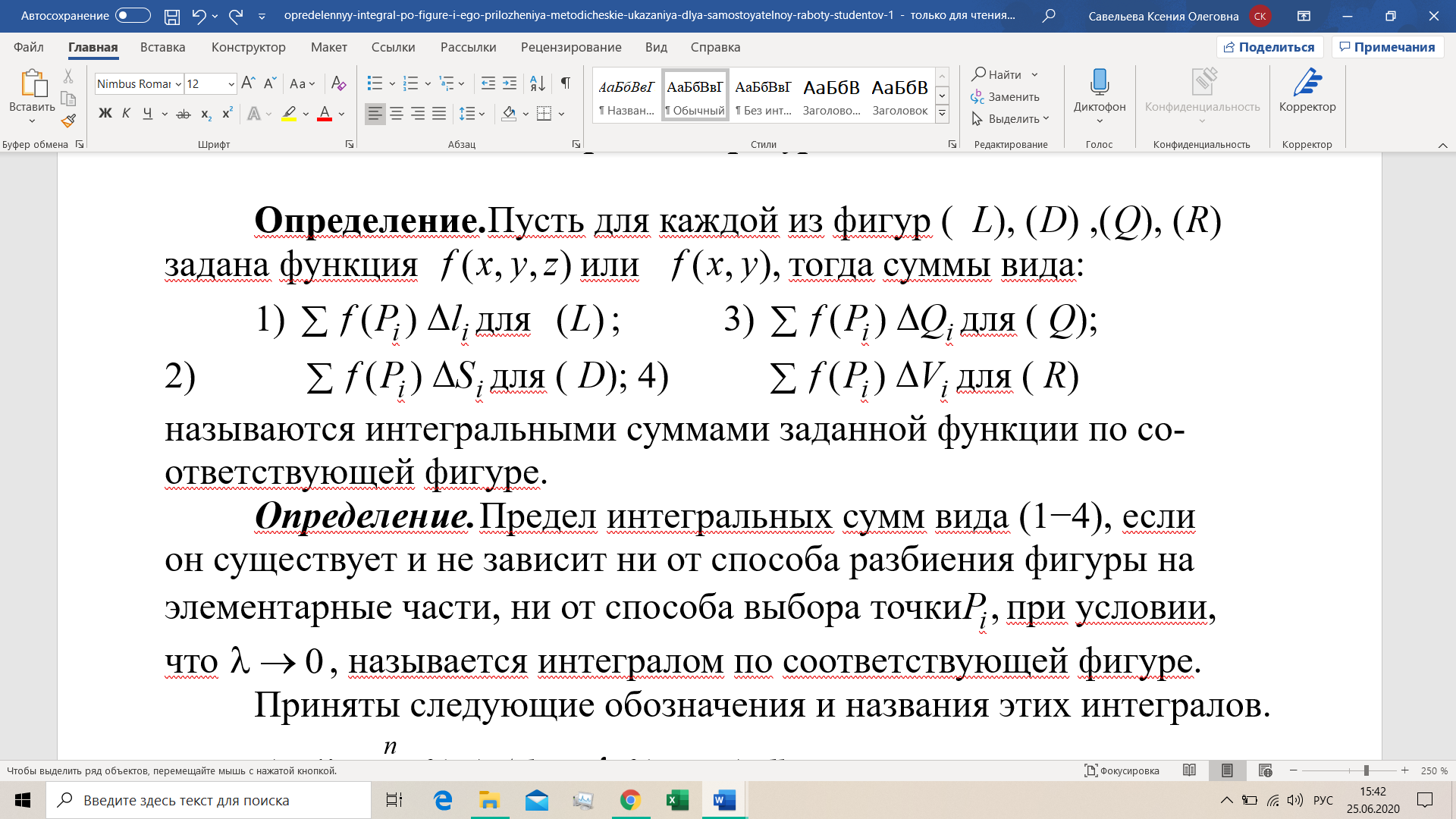
Понятие интеграла по фигуре
Лямда – диаметр фигуры. Свойства интеграла по фигуре: · Интеграл от суммы функций равен сумме интегралов. Выполняется при условии, что обе функции интегрируемы · Вынесение константы за знак интеграла · Разбие области на части соответсвует сумме интегралов · Если подынтегральная функция равна 1, то интеграл по фигуре численно равен мере фигуры
Поверхностный. Мы рассматривали фигуры пяти видов: отрезок, дугу кривой, поверхность, плоскую область и тело. Следовательно, мы получим пять видов интегралов по фигуре:
1. Если фигура (Ф) является отрезком [a,b], то интеграл называют определенным интегралом и обозначают
2. Если фигура (Ф) является дугой кривой (l), то интеграл по такой фигуре называют криволинейным интегралом 1-го рода и обозначают
Здесь Dlk – меры ячеек, в данном случае длины частичных дуг (Dlk); d – максимальный из diam (Dlk).
3. Если фигура (Ф) является поверхностью (s), то интеграл по такой фигуре называют поверхностным интегралом 1-го рода и обозначают
4. Если фигура (Ф) является плоской областью (S), то интеграл по такой фигуре называют двойным интегралом и обозначают
5. Если фигура (Ф) является телом (V), то интеграл по такой фигуре называют тройным интегралом и обозначают
dS = dx × dy,
Аналогичная форма записи принята и для тройного интеграла
Скалярное поле 3.1 Скалярное поле – это область пространства, в которой задана скалярная функция f (x, y, z), называемая функцией поля. Поверхность уровня – это множество точек поля, в которых функция поля f(x,y,z) принимает постоянное значение c, образуя поверхность с уравнением f(x,y,z)=c. Если скалярное поле плоское, например, находится в плоскости XOY, то его функция поля f (x, y) зависит от двух переменных x и y, а множество точек, в которых f (x, y) = c, образуют линию уровня. (Определение) Линией уровня функции z = f (x, y) называется линия f (x,y)=c на плоскости XOY, в точках которой функция сохраняет свое постоянное значение (z=c).
(Вывод) Понятие производной поля по направлению вводят для характеристики скорости изменения поля f (x, y, z) в направлениивектора Векторное поле 4.1 Векторное поле – это область пространства, в каждой точке M которой задан вектор Примеры векторных полей: 1) Пусть на материальную точку в области D действует сила 2) Пусть в области D происходит течение жидкости и в каждой точке M задан вектор 3) Поместим заряд + q в начало координат. Тогда сила, с которой этот заряд действует на единичный положительный заряд, помещенный в точку M, определяется по закону Кулона:
Вычисления. Ориентированная поверхность – это поверхность, в каждой точке которой выбрано направление нормали с помощью единичного вектора n(М), где n(M) является непрерывной вектор-функцией точки М. Поток векторного поля Потоком векторного поля a через ориентировочную поверхность (
Записи: 1) 2) 3) Вычисление: 1) По формуле 2) Методом проектирования на 3 плоскости
а) в подынтегральной функции заменить x его значением x=x(y,z) на поверхности б) учесть, что d в) вычислить получившийся двойной интеграл по проекции Другие вычисляются аналогично 3) Методом проектирования на одну плоскость Воспользуемся параметрическим уравнением поверхности Нормальный вектор поверхности: Элемент площади
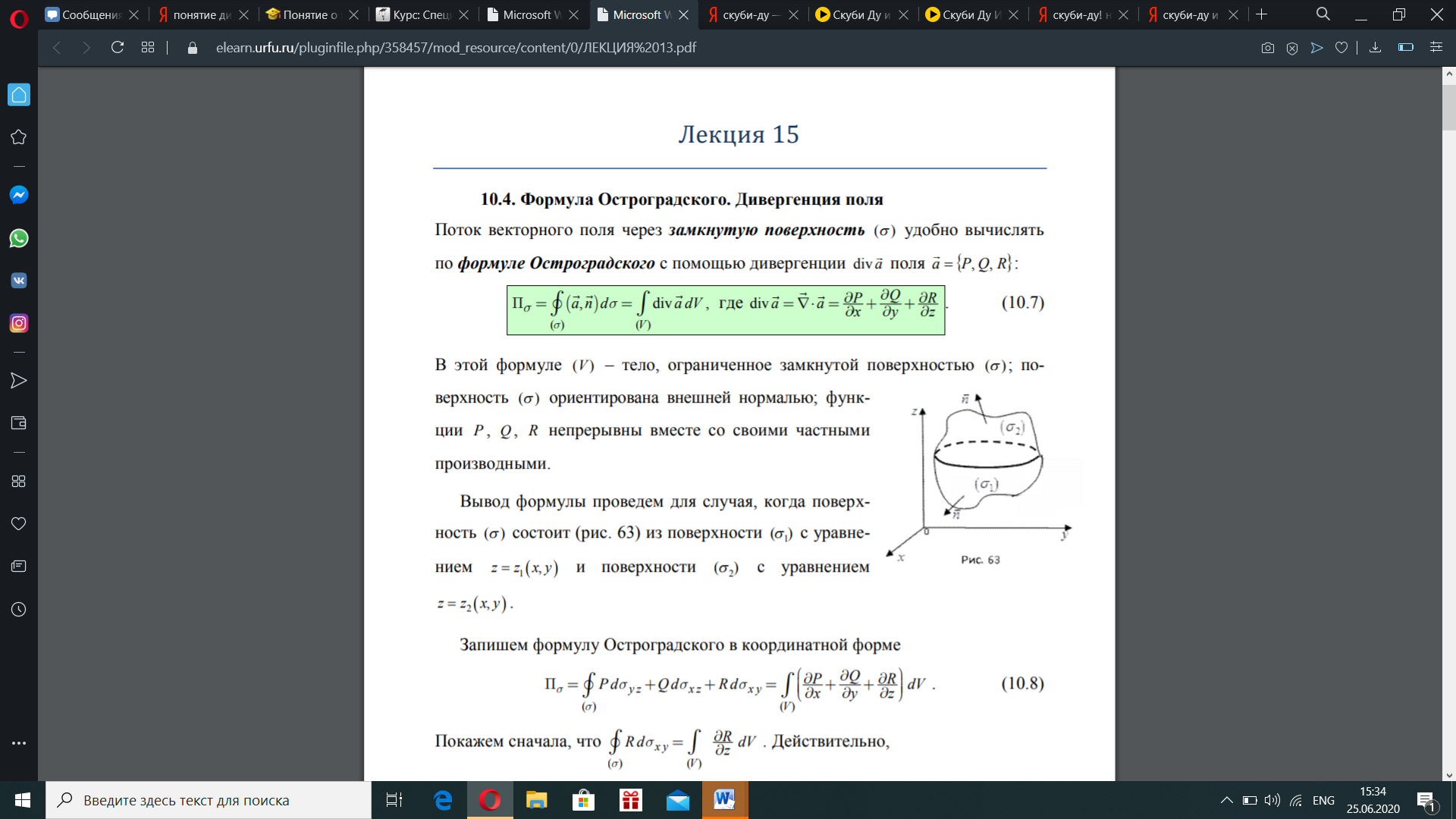
4.3 . Формула Остроградского и понятие дивергенции. Инвариантное определение дивергенции, ее свойства. Формула Остроградского Поток векторного поля через замкнутую поверхность (s) удобно вычислять по формуле Остроградского с помощью дивергенции div a поля a = {P, Q, R}
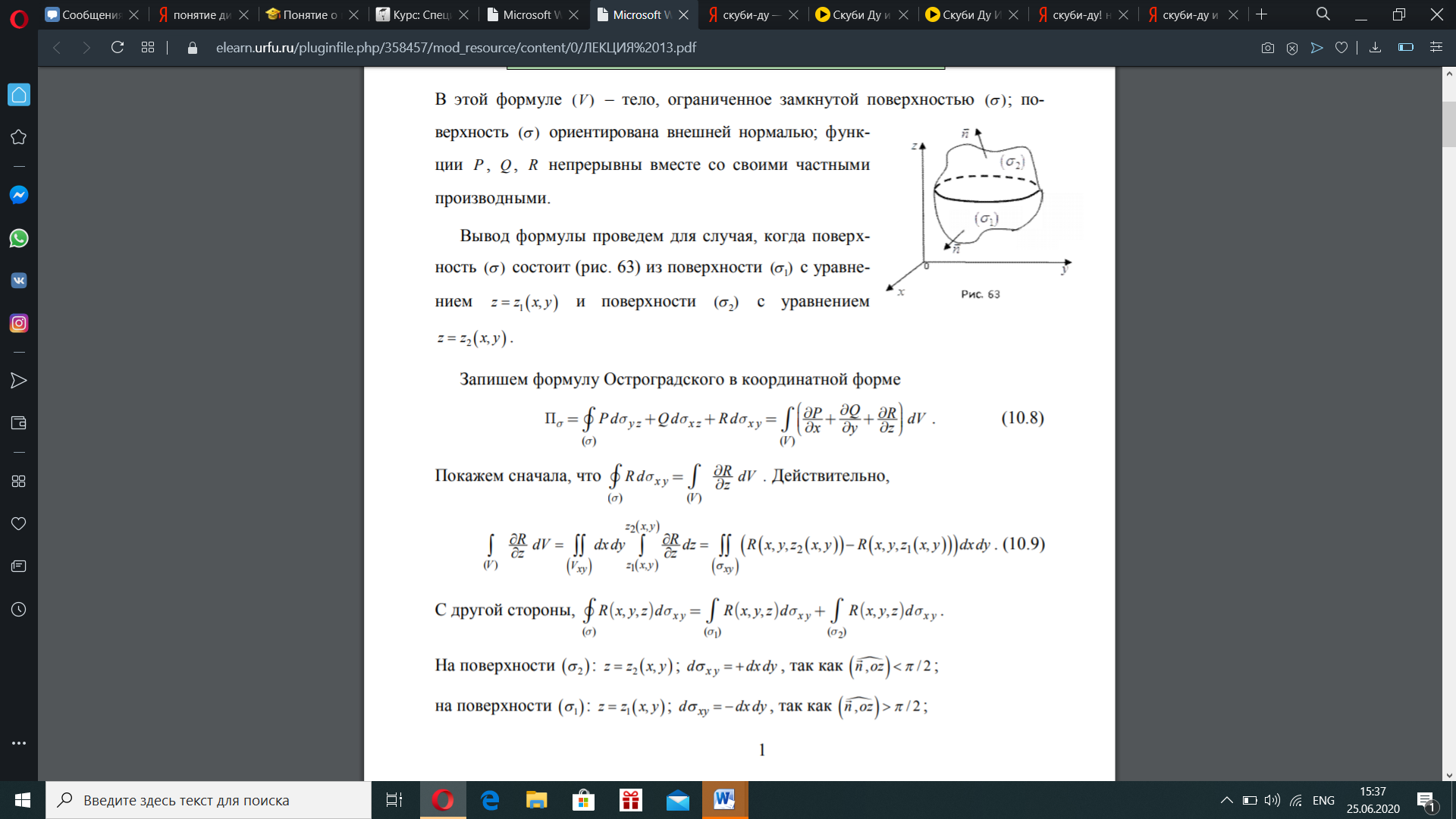
В этой формуле () V – тело, ограниченное замкнутой поверхностью (s); поверхность (s) ориентирована внешней нормалью; функции P, Q, R непрерывны вместе со своими частными производными. Запишем формулу Остроградского в координатной форме
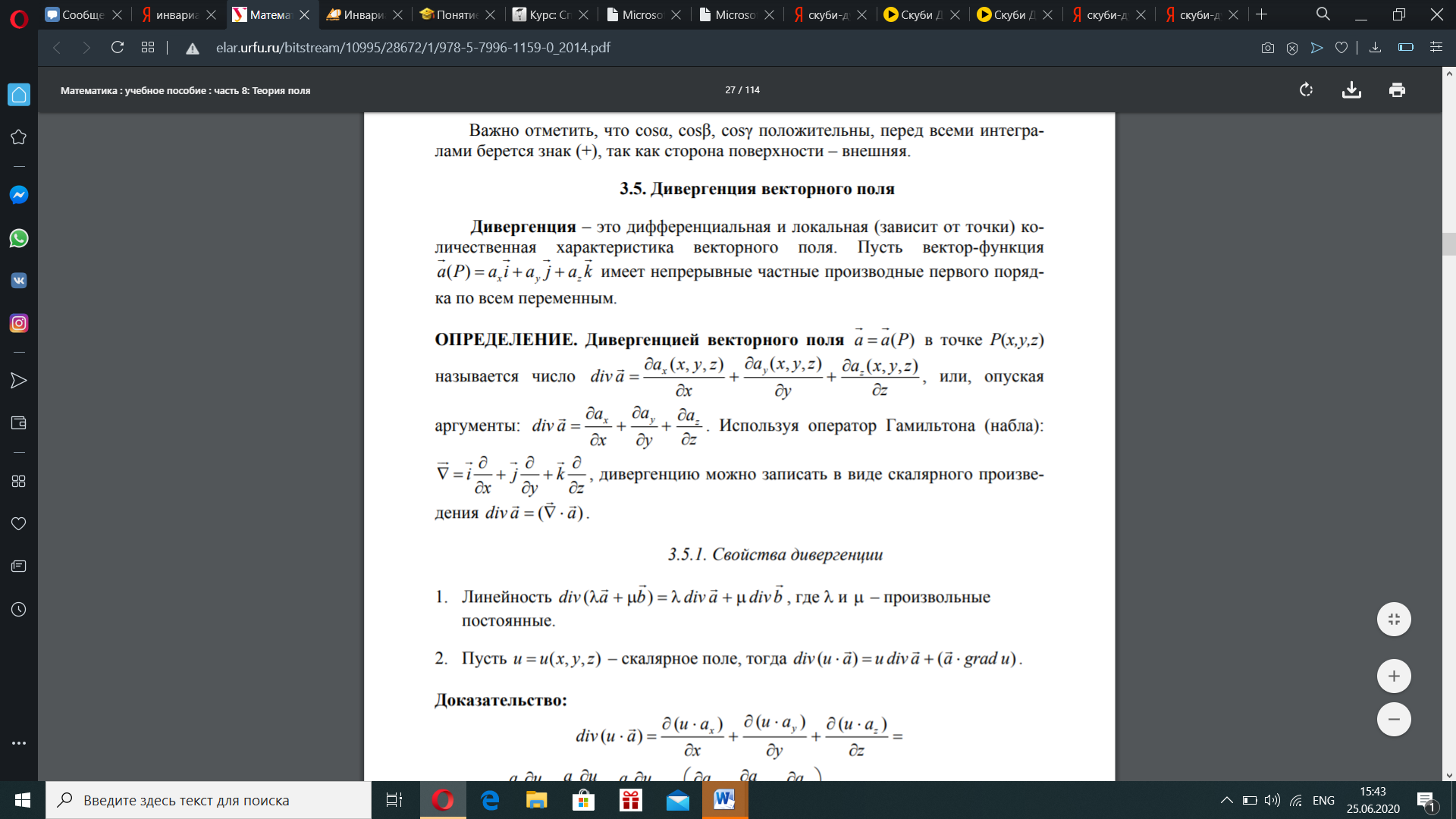
Понятие дивергенции Дивергенция – это дифференциальная и локальная (зависит от точки) количественная характеристика векторного поля. Пусть вектор-функция
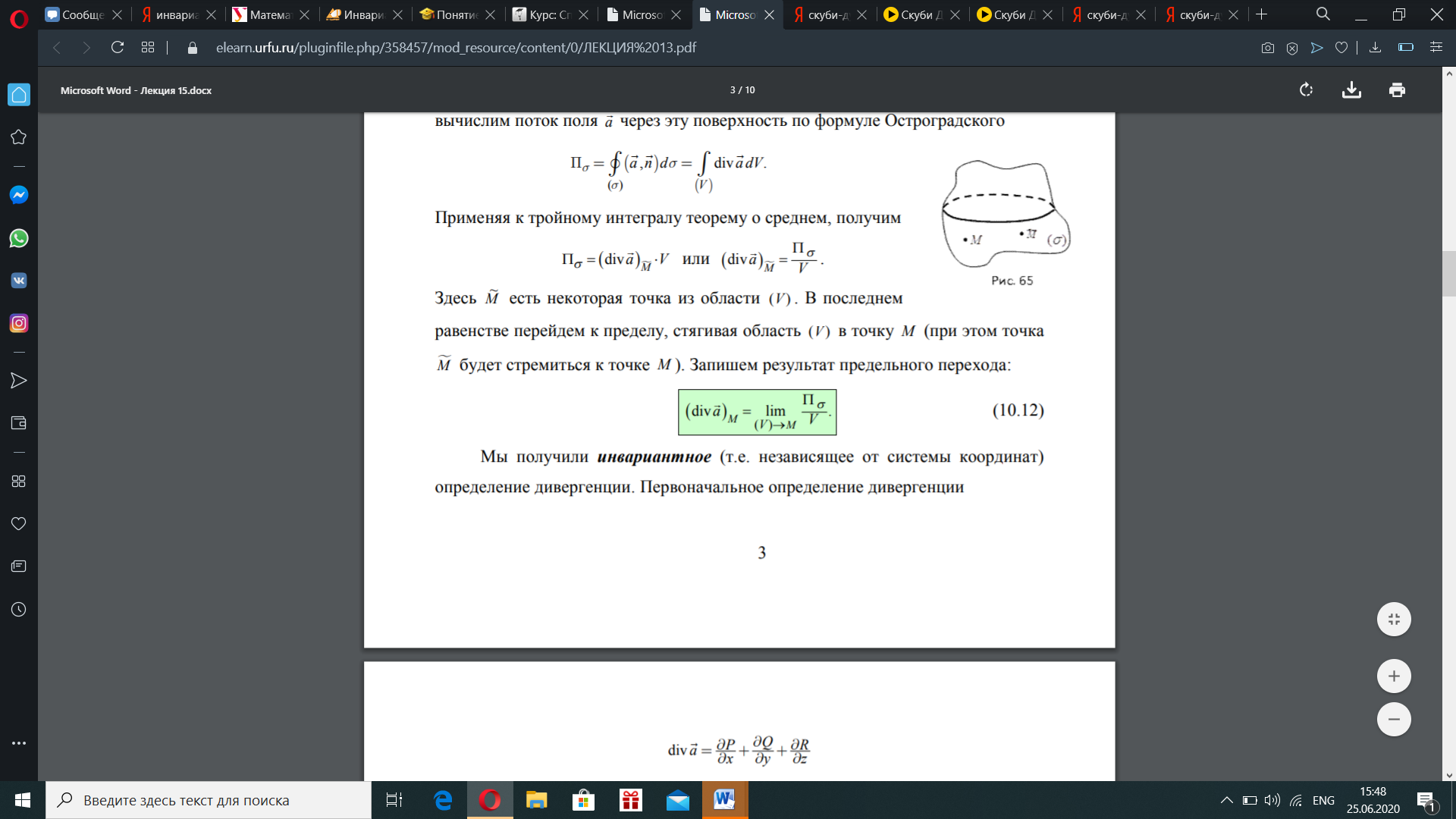
Мы получили инвариантное (т.е. независящее от системы координат) определение дивергенции.
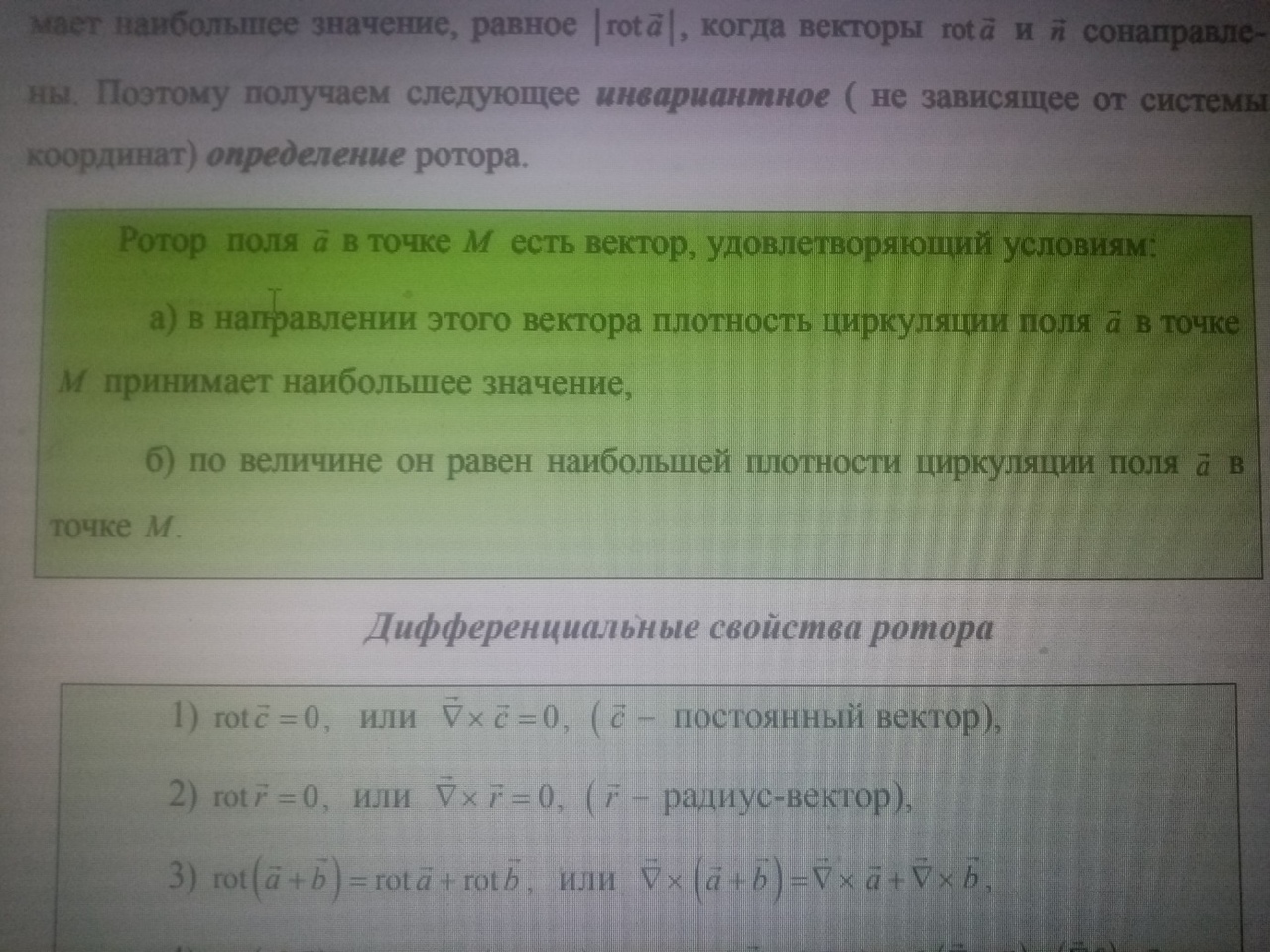
Понятие Ротора: Физический смысл ротора: Таким образом, ротор поля линейных скоростей в любой точке равен удвоенному вектору угловой скорости. В произвольном поле его ротор, вычисленный в точке M, также характеризует вращательную способность поля в этой точке. Инвариантное определение ротора:
Гармонические поля. 1)Векторное поле называется потенциальным (безвихревым полем), если в каждой его точке ротация равна нулю:
2) Скалярный потенциал векторного поля A {\displaystyle \mathbf {A} } А — это скалярная функция ϕ {\displaystyle \phi } Фи такая, что во всех точках области определения поля А=grad(фи) A = grad ϕ, {\displaystyle \mathbf {A} =\operatorname {grad} \,\phi,} Где grad(фи) grad ϕ {\displaystyle \operatorname {grad} \phi } обозначает градиент ϕ {\displaystyle \phi } Фи.
Непрерывное векторное поле в односвязной области трёхмерного пространства потенциально тогда и только тогда, когда оно безвихревое, то-есть тогда,когда Ротор равен 0. 3)Векторное поле называется соленоидальным или вихревым, если через любую замкнутую поверхность S его поток равен нулю: 4) Гармоническим называется поле, для которого и ротор и дивергенция равны нулю.
∫ S a → ⋅ d s → = 0 {\displaystyle \int \limits _{S}{\vec {a}}\cdot {\vec {ds}}=0} 4.8. Повторные операции теории поля. Оператор Гамильтона Ñ. Запись основных характеристик скалярного и векторного поля с помощью Ñ. Правила действия с Ñ Запись основных характеристик скалярного и векторного поля с помощью Ñ.
Правила действия с Ñ
Ряды 1.1. Числовой ряд, его сходимость, сумма. Признаки сходимости знакоположительных рядов. Знакочередующийся ряд, признак Лейбница. Знакопеременные ряды, абсолютная и условная сходимости. Комплексные числовые ряды. 1.2. Степенные ряды и их свойства. Ряды Тейлора и их применение к вычислению значений функции, к вычислению определенных интегралов, к решению дифференциальных уравнений. 1.3. Разложение периодической функции в тригонометрический ряд Фурье. Ряд Фурье для четной и нечетной функции. Разложение функции, заданной на отрезке в ряд Фурье. Ряд Фурье в комплексной форме. Спектральные характеристики периодической функции. 2. Интегралы по фигуре 2.1. Понятие фигуры, её диаметра, меры. Вычисление массы фигуры. Понятие интеграла по фигуре, его свойства и приложения. 2.2. Конкретные виды интеграла по фигуре: криволинейный, двойной, тройной, поверхностный. 2.3. Вычисление криволинейного интеграла 1-го рода. 2.4. Вычисление двойного и тройного интеграла в прямоугольной и криволинейной системах координат. 2.5. Вычисление поверхностного интеграла 1-го рода. Скалярное поле 3.1. Скалярное поле. Поверхности (линии) уровня. 3.2. Производная поля по направлению. 3.3. Градиент скалярного поля: его свойства, инвариантное определение. Векторное поле 4.1. Примеры векторных полей. Векторные линии. 4.2. Поток поля через ориентированную поверхность: различные формы записи, способы вычисления. 4.3. Формула Остроградского и понятие дивергенции. Инвариантное определение дивергенции, ее свойства. 4.4. Вычисление работы в силовом поле. Линейный интеграл поля и циркуляция: свойства, различные формы записи, способы вычисления. 4.5. Формула Стокса. Понятие ротора: его физический смысл. 4.6. Условие независимости линейного интеграла поля от формы пути интегрирования. 4.7. Потенциальное поле, отыскание скалярного потенциала. Соленоидальное поле, гармонические поля. 4.8. Повторные операции теории поля. Оператор Гамильтона Ñ. Запись основных характеристик скалярного и векторного поля с помощью Ñ. Правила действия с Ñ
1.Ряды 1.1 Числовой ряд, его сходимость, сумма Числовой ряд – это сумма бесконечного числа членов числовой последовательности вида
где числа а1, а2, а3, …. an – называются членами ряда, член аn – общим или n-ым членом ряда. Сумма конечного числа к первых членов ряда – называется к - ой частичной суммой ряда – S n Если существует конечный предел последовательности частичной суммы ряда, то ряд называется сходящимся, а число S – называется суммой ряда
Если же предел последовательности частичных сумм равен ∞ или не существует, то ряд называется расходящимся.
Признаки сходимости знакоположительных рядов. · Th 1. Необходимый признак сходимости ряда Если ряд сходится, то предел общего члена равен 0 Следствие: Если предел общего члена не равен 0, то ряд расходится. · Операции с числовыми рядами Th 2 Если сходится ряд, полученный из данного ряда путем отбрасывания конечного числа первых членов, то данный ряд тоже сходится, обратная теорема тоже справедлива. · Т h 3 Если ряд · Th 4 Если два ряда · Th 5 первый признак сравнения Пусть даны ряды · Th 6 второй признак сравнения Пусть даны ряды · Th 7 предельный признак сравнения рядов Пусть даны два знакоположительных ряда. Если существует конечный, отличный от нуля предел
· Признак Даламбера Пусть дан ряд То если: 1) l < 1, ряд сходится 2) l > 1, ряд расходится 3) l = 1, необходимы дополнительные исследования
· Радикальный признак Коши
Пусть дан ряд с положительными членами и существует конечный или бесконечный предел То если: 1) l < 1, ряд сходится 2) l > 1, ряд расходится 3) l = 1, необходимы дополнительные исследования
· Интегральный признак сходимости Коши Пусть члены ряда Тогда справедливы следующие утверждения: 1) если несобственный интеграл 2) если несобственный интеграл
Знакочередующийся ряд Знакочередующийся ряд — это ряд вида
Теорема Лейбница (признак Лейбница) Знакочередующийся ряд сходится, если: 1) последовательность абсолютных величин членов ряда монотонно убывает: 2) общий член ряда стремится к нулю, то есть
Знакопеременный ряд
Ряд называется знакопеременным, если среди его членов имеются как положительные так и отрицательные члены. Знакочередующиеся ряды являются частным случаем знакопеременных рядов.
Теорема (достаточный признак сходимости знакопеременного ряда)
Пусть дан знакопеременный ряд
Если сходится ряд составленный из абсолютных величин данного ряда
то сходится и сам знакопеременный ряд.
|
|||||||||
|
Последнее изменение этой страницы: 2021-06-14; просмотров: 91; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.77.114 (0.169 с.) |
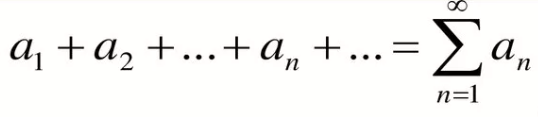
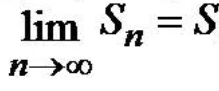
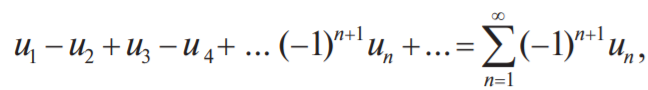
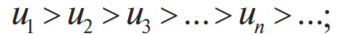
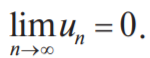
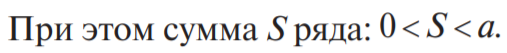
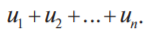
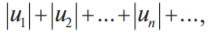
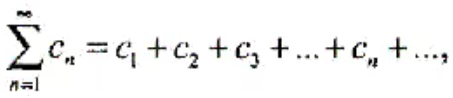

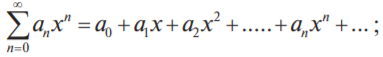
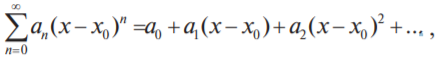
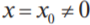 , то он абсолютно сходится при всех значениях x, удовлетворяющих неравенству
, то он абсолютно сходится при всех значениях x, удовлетворяющих неравенству 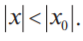
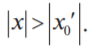
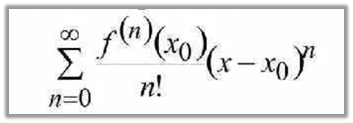
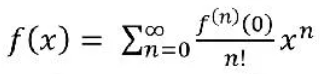


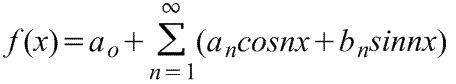 (1)
(1)


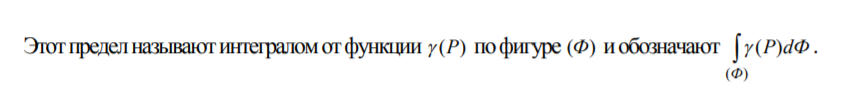
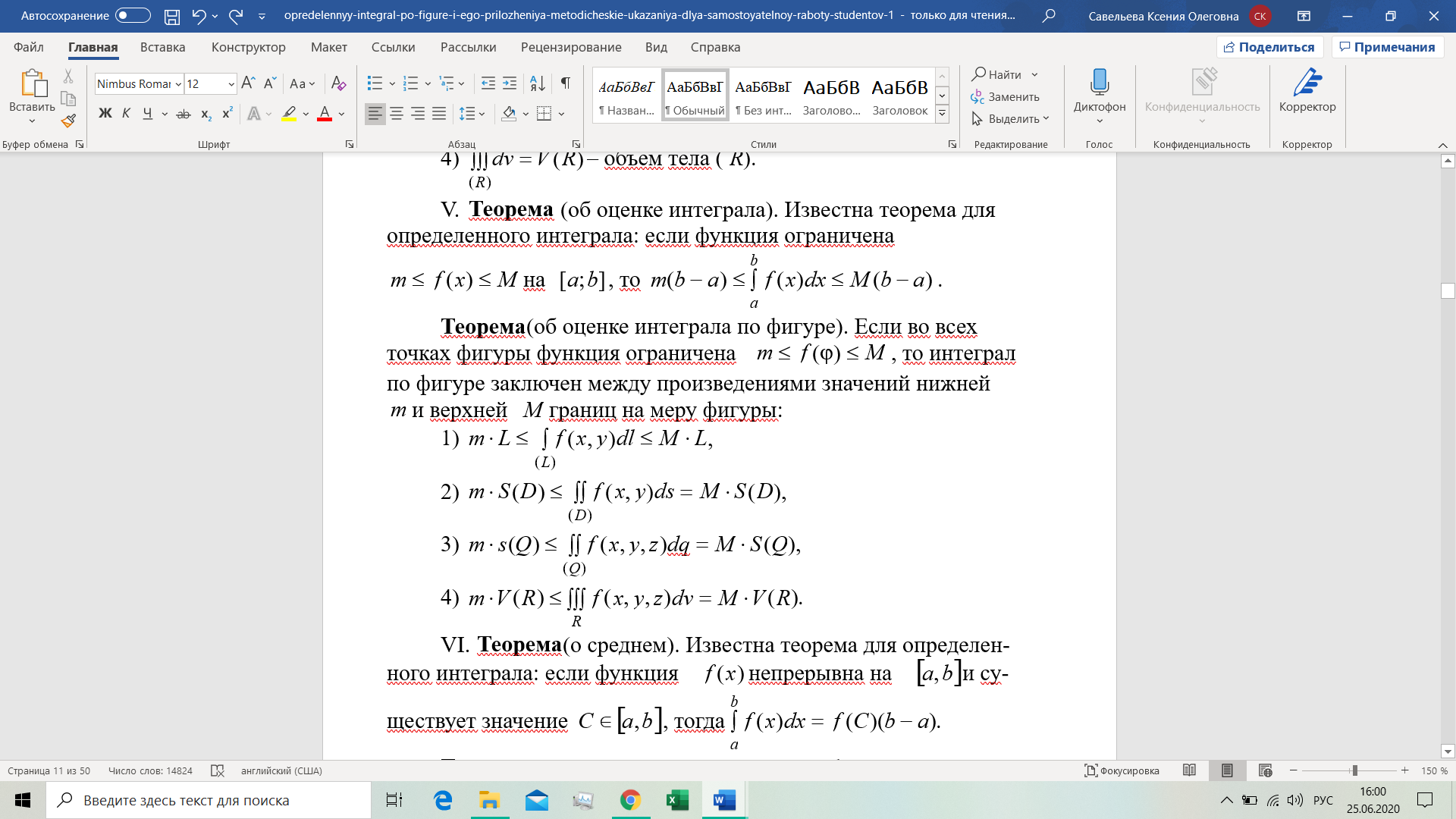
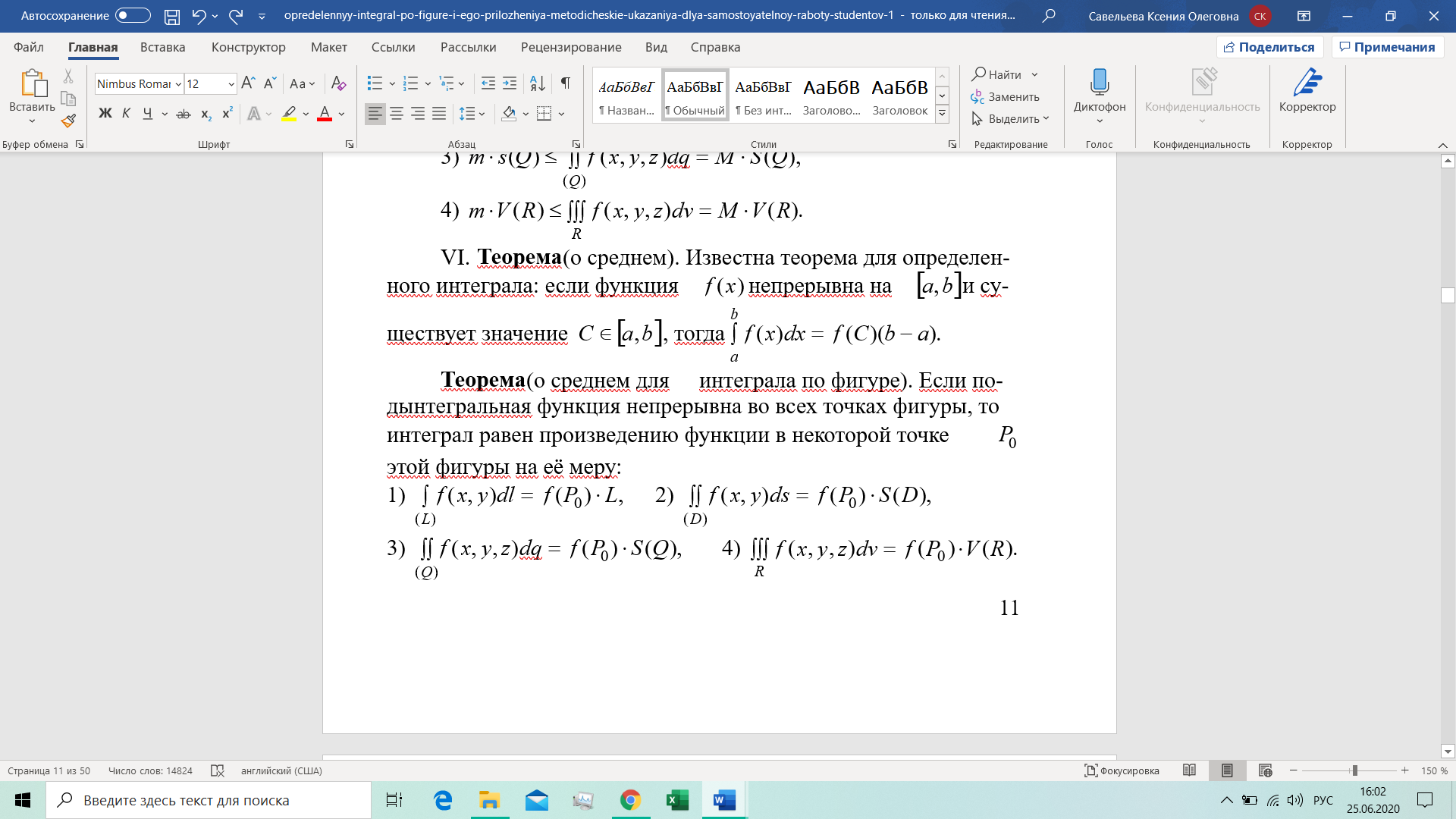
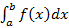 . По определению
. По определению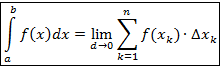
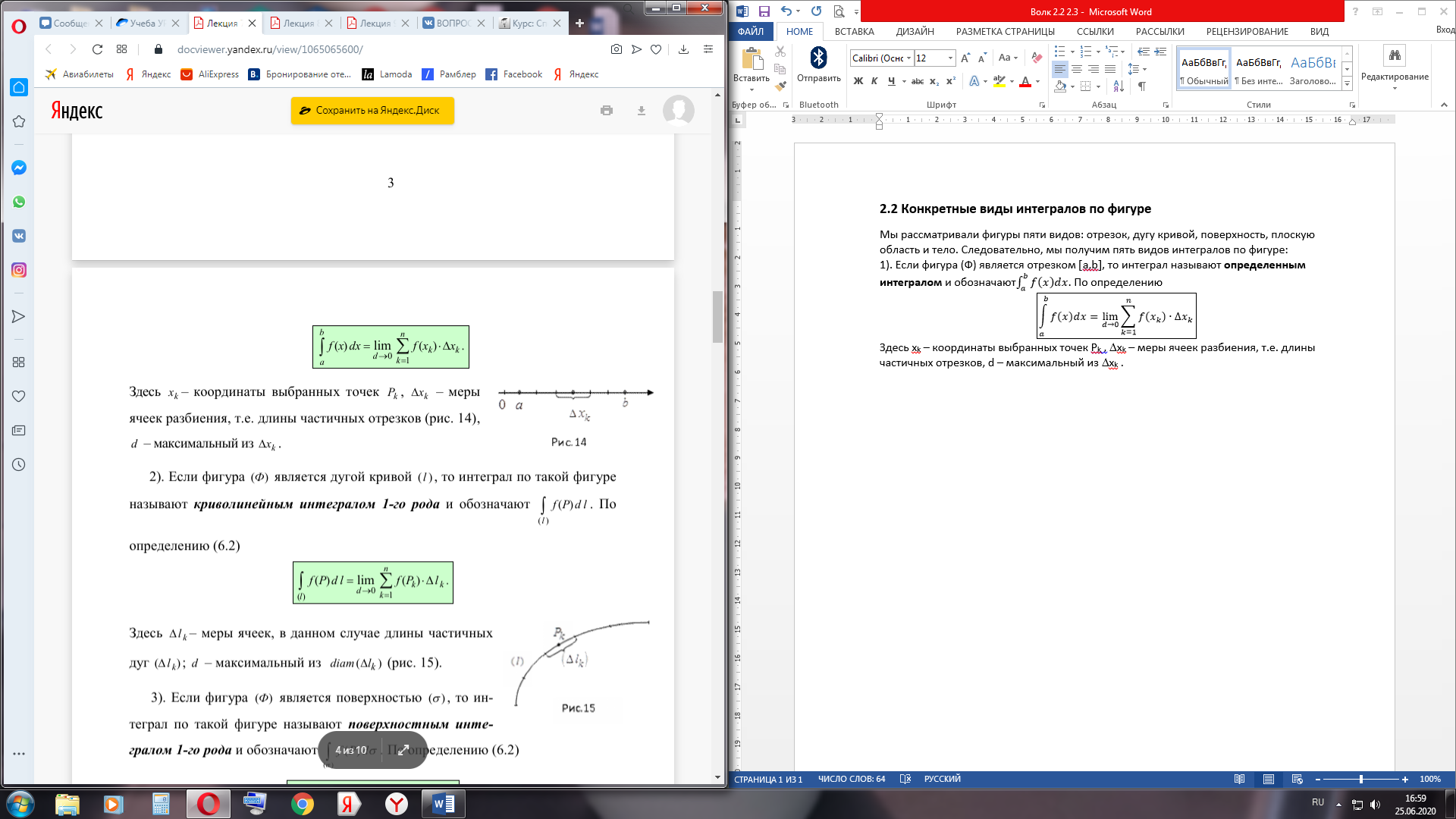 Здесь xk – координаты выбранных точек Pk, Dxk – меры ячеек разбиения, т.е. длины частичных отрезков, d – максимальный из Dxk.
Здесь xk – координаты выбранных точек Pk, Dxk – меры ячеек разбиения, т.е. длины частичных отрезков, d – максимальный из Dxk.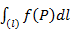 . По определению
. По определению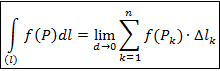
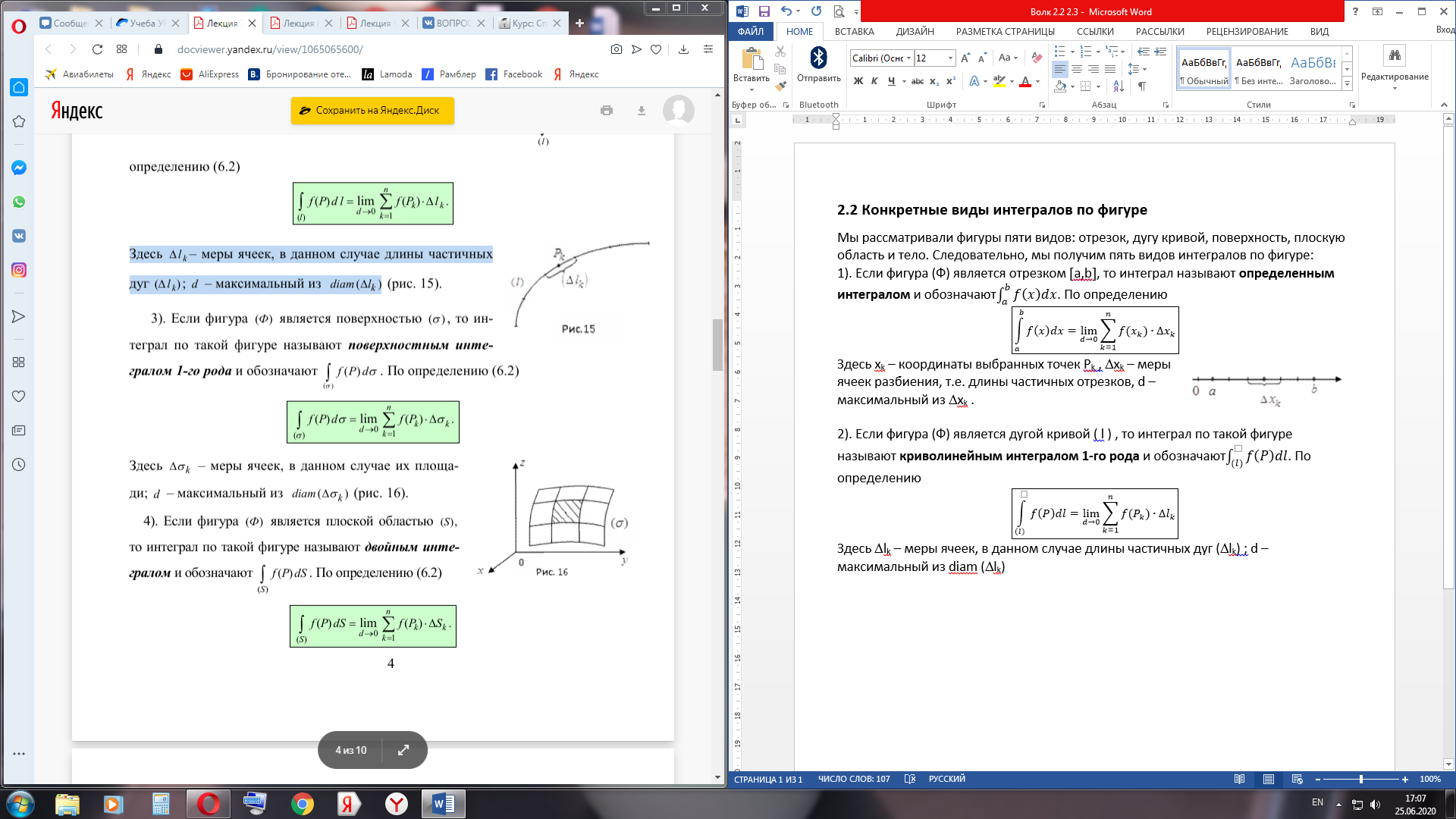
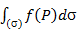 . По определению
. По определению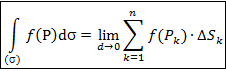
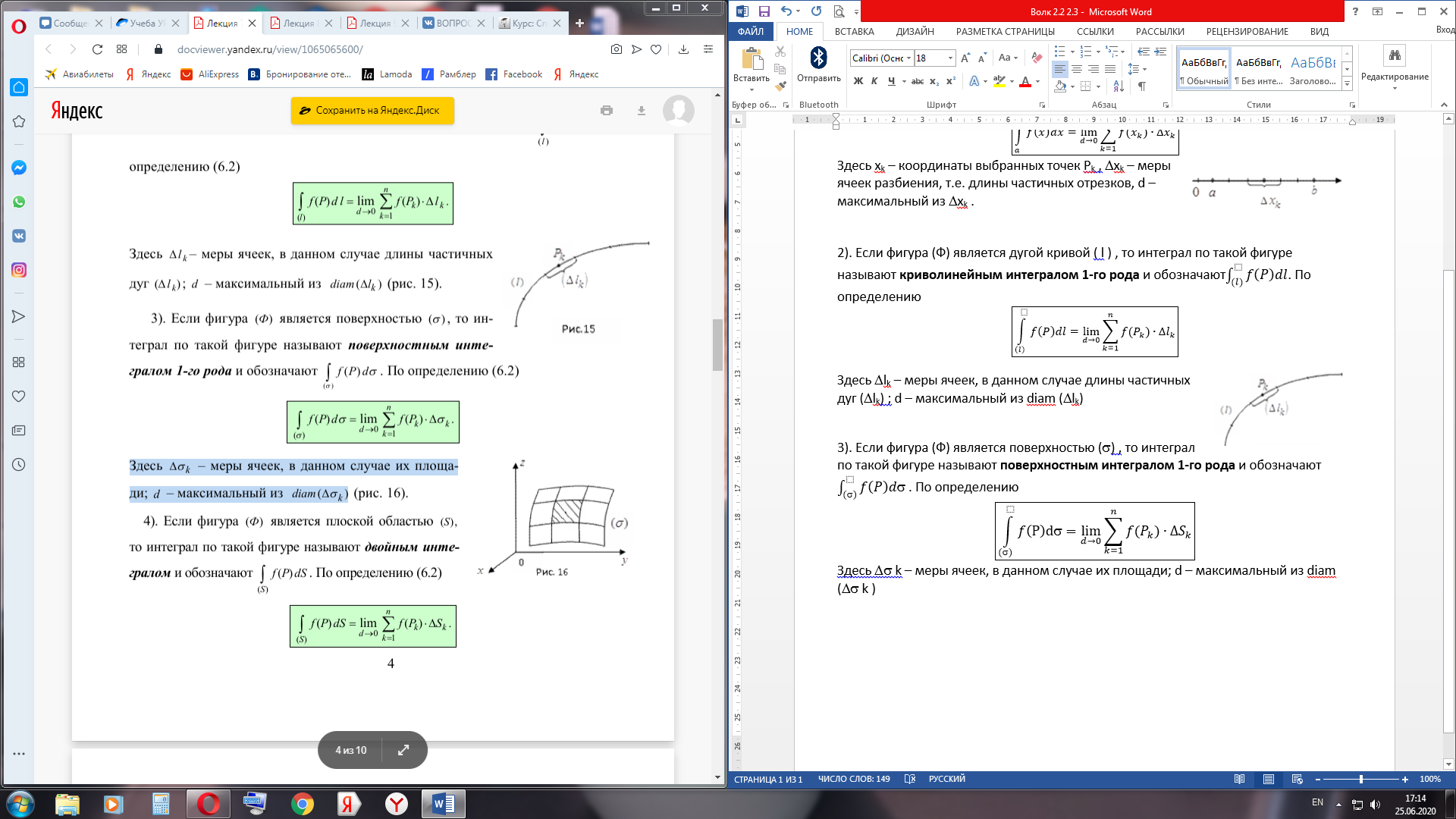 Здесь Dsk – меры ячеек, в данном случае их площади; d – максимальный из diam (Dsk).
Здесь Dsk – меры ячеек, в данном случае их площади; d – максимальный из diam (Dsk).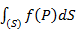 . По определению
. По определению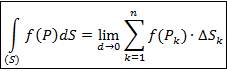
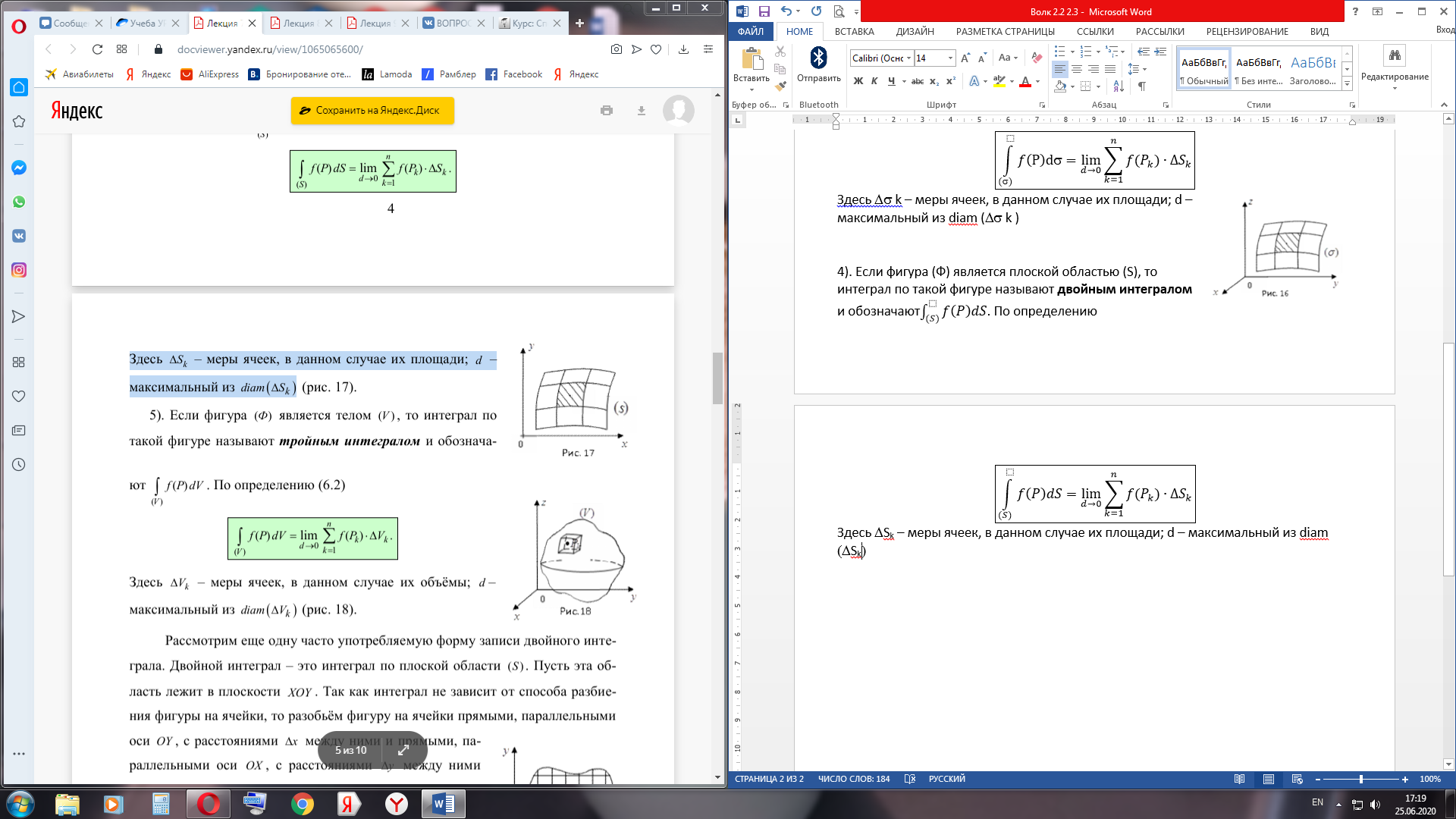 Здесь DSk – меры ячеек, в данном случае их площади; d – максимальный из diam (DSk).
Здесь DSk – меры ячеек, в данном случае их площади; d – максимальный из diam (DSk).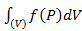 . По определению
. По определению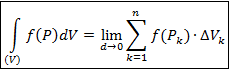
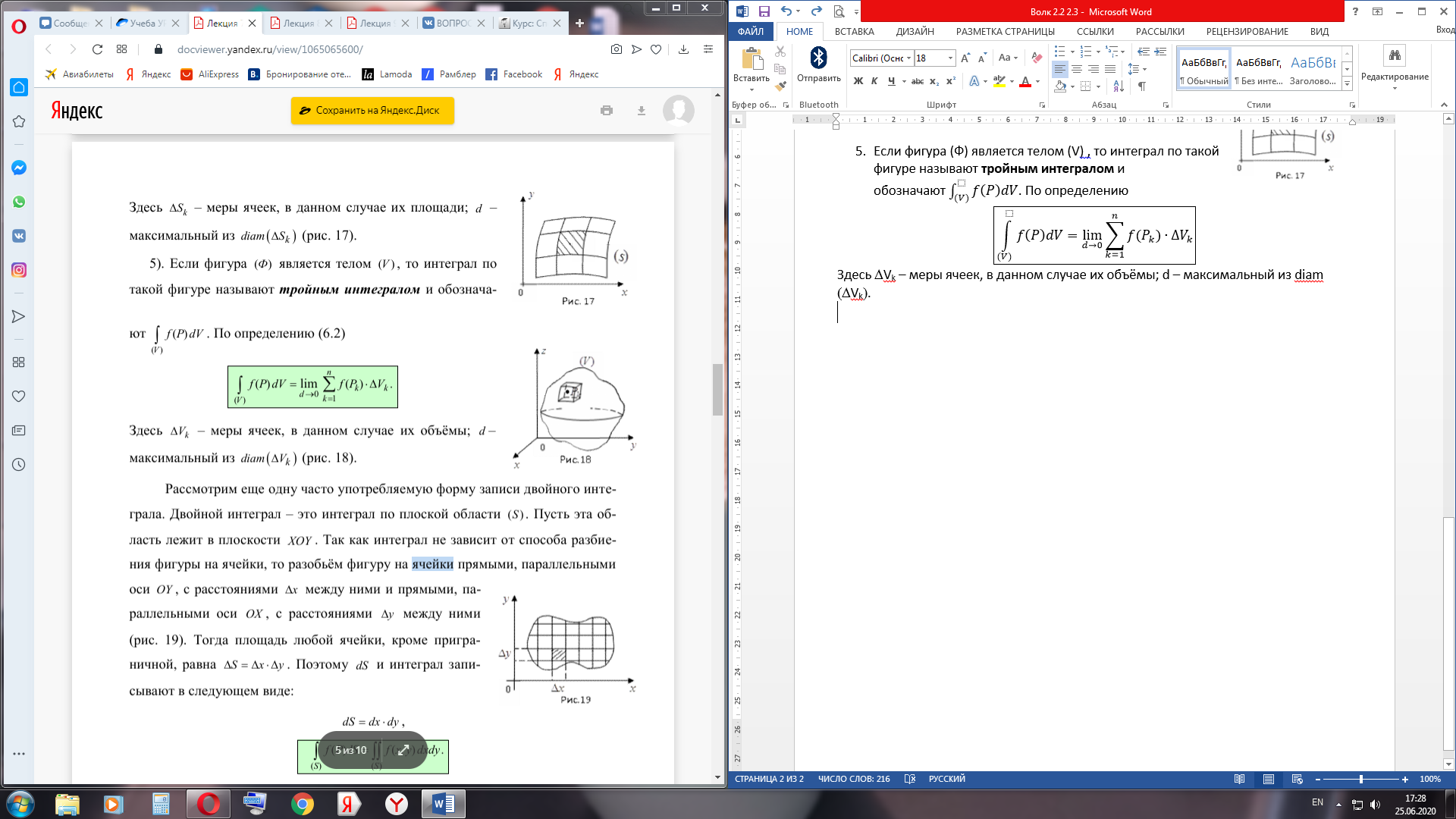 Здесь DVk – меры ячеек, в данном случае их объёмы; d – максимальный из diam (DVk).
Здесь DVk – меры ячеек, в данном случае их объёмы; d – максимальный из diam (DVk).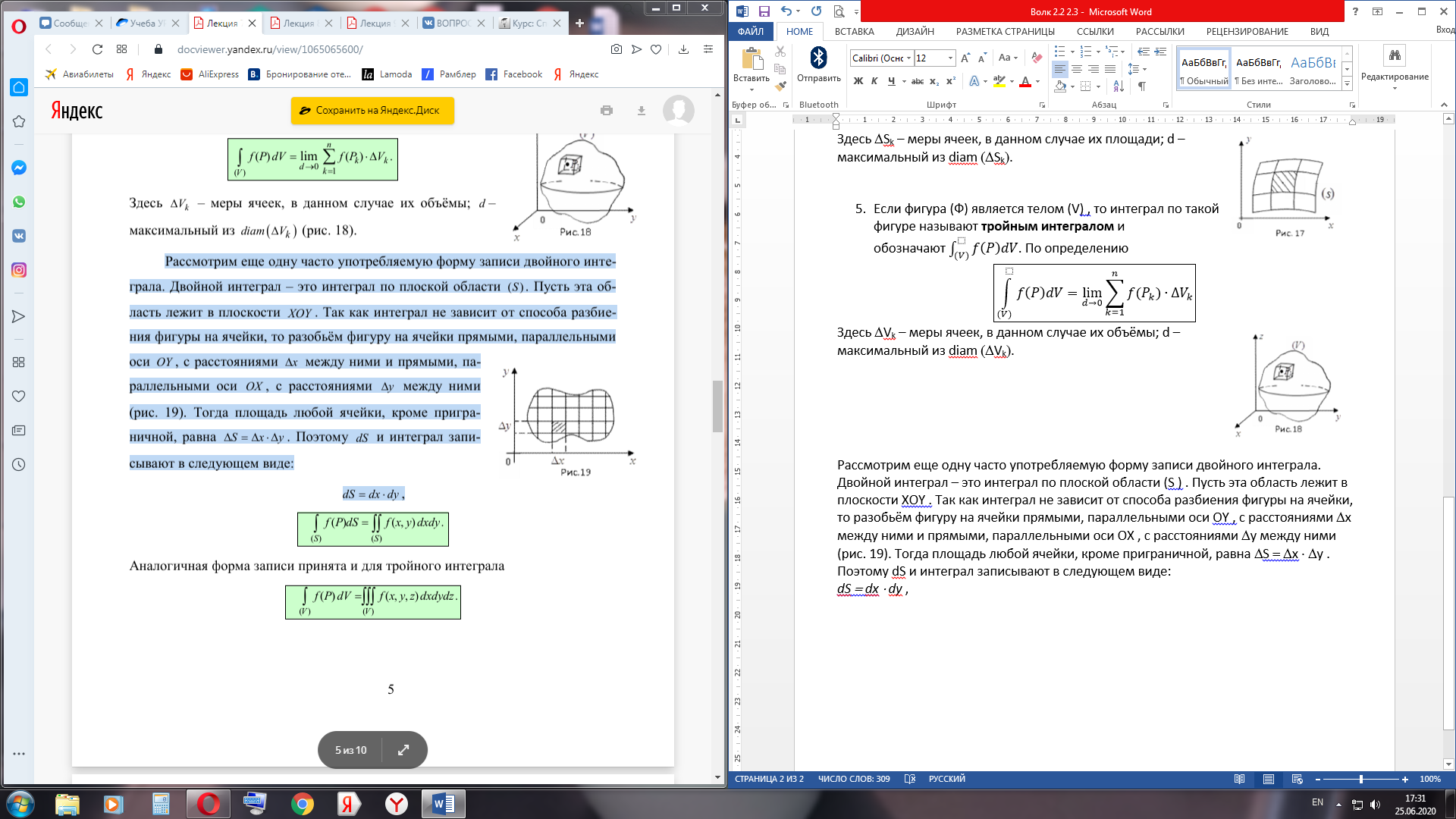 Рассмотрим еще одну часто употребляемую форму записи двойного интеграла. Двойной интеграл – это интеграл по плоской области (S). Пусть эта область лежит в плоскости XOY. Так как интеграл не зависит от способа разбиения фигуры на ячейки, то разобьём фигуру на ячейки прямыми, параллельными оси OY, с расстояниями Dx между ними и прямыми, параллельными оси OX, с расстояниями Dy между ними (рис. 19). Тогда площадь любой ячейки, кроме приграничной, равна DS = Dx × Dy. Поэтому dS и интеграл записывают в следующем виде:
Рассмотрим еще одну часто употребляемую форму записи двойного интеграла. Двойной интеграл – это интеграл по плоской области (S). Пусть эта область лежит в плоскости XOY. Так как интеграл не зависит от способа разбиения фигуры на ячейки, то разобьём фигуру на ячейки прямыми, параллельными оси OY, с расстояниями Dx между ними и прямыми, параллельными оси OX, с расстояниями Dy между ними (рис. 19). Тогда площадь любой ячейки, кроме приграничной, равна DS = Dx × Dy. Поэтому dS и интеграл записывают в следующем виде: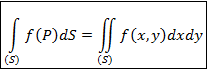
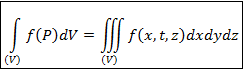
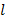 . Пусть задана точка M и вектор l, выходящий из точки M (рис. 53). Рассмотрим точку M 1, лежащую на векторе l, и величину
. Пусть задана точка M и вектор l, выходящий из точки M (рис. 53). Рассмотрим точку M 1, лежащую на векторе l, и величину 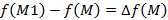 – приращение функции поля f (M) в точке M в направлении вектора l.
– приращение функции поля f (M) в точке M в направлении вектора l.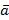 (M).
(M).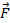 (M). Тогда в области D определено векторное поле
(M). Тогда в области D определено векторное поле 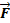 ((M).
((M).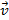 (M) скорости частицы жидкости. Тогда в области D определено векторное поле скоростей жидкости
(M) скорости частицы жидкости. Тогда в области D определено векторное поле скоростей жидкости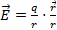 , где r r – вектор, идущий из начала координат в точку M (радиус-вектор точки M), r – его длина. Имеем векторное поле напряженностей
, где r r – вектор, идущий из начала координат в точку M (радиус-вектор точки M), r – его длина. Имеем векторное поле напряженностей 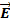 (M), создаваемое зарядом q.
(M), создаваемое зарядом q.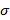 ) с единичным нормальным вектором n называют величину:
) с единичным нормальным вектором n называют величину: 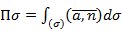
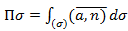 – векторная форма записи
– векторная форма записи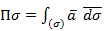 - векторная форма записи
- векторная форма записи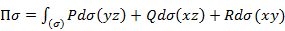 – координатная форма записи
– координатная форма записи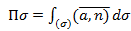
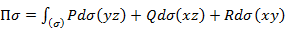 =
= 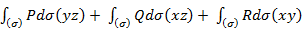

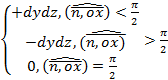
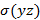
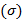 :
: 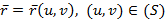
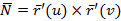
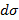 :
: 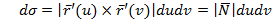
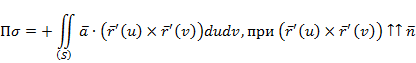
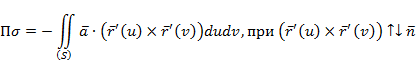
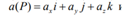 имеет непрерывные частные производные первого порядка по всем переменным
имеет непрерывные частные производные первого порядка по всем переменным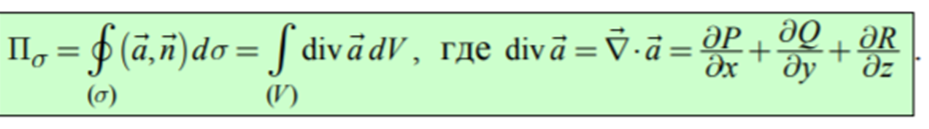
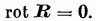
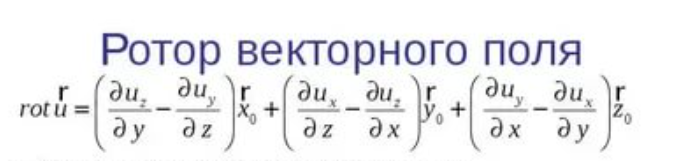
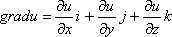

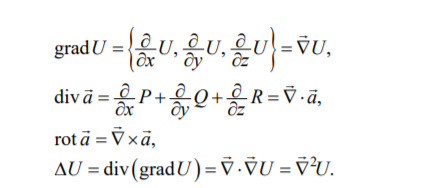

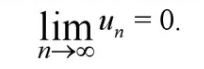
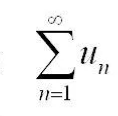 сходится и его сумма S, то ряд
сходится и его сумма S, то ряд 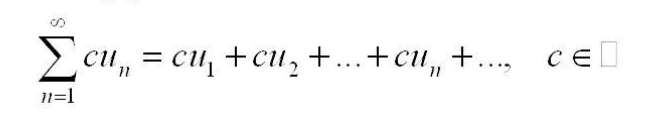 , где с= const тоже сходится и его сумма c*S
, где с= const тоже сходится и его сумма c*S 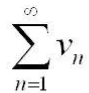 и
и 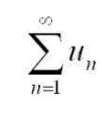 сходятся соответственно и их суммы равны
сходятся соответственно и их суммы равны 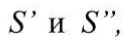 то ряды сходятся к
то ряды сходятся к 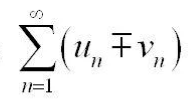 и сумма каждого ряда равна
и сумма каждого ряда равна 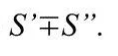
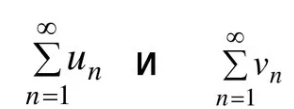 и ряд с большими членами сходится, то и ряд с меньшими членами также сходится.
и ряд с большими членами сходится, то и ряд с меньшими членами также сходится.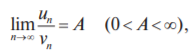 то ряды сходятся или расходятся одновременно.
то ряды сходятся или расходятся одновременно.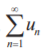 с положительными членами и существует конечный или бесконечный предел
с положительными членами и существует конечный или бесконечный предел 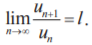
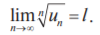
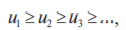 и пусть f (х) — такая непрерывная невозрастающая функция, что
и пусть f (х) — такая непрерывная невозрастающая функция, что 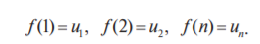
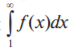 сходится, то сходится и ряд;
сходится, то сходится и ряд;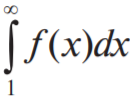 расходится, то расходится и ряд.
расходится, то расходится и ряд.


