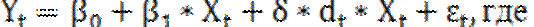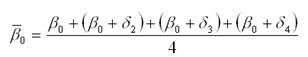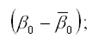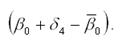Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интерпретация параметров парной линейной эконометрической модели.⇐ ПредыдущаяСтр 11 из 11
Параметр а1 показывает, на сколько единиц изменится значение Y при изменении Х на одну единицу. При этом обязательно надо указывать точный характер изменения (увеличение, уменьшение) конкретного числового значения и единиц измерения. Параметр а0 показывает, на сколько единиц график регрессии смещен вверх (вниз) при Х= 0. Экономическая интерпретация (если она допустима) – Значение Y при нулевом значении X. Часто экономическая интерпретация отсутствует. Поэтому, прежде чем давать интерпретацию а0 и а1 следует убедиться в высоком качестве уравнения регрессии. Например:
Сущность проверки статистической гипотезы заключается в том, чтобы установить, согласуются или нет данные наблюдений и выдвинутая гипотеза. Если при проверке гипотезы выборочные данные противоречат гипотезе Н0, то она отклоняется, в противном случае не отклоняется. При этом возможны ошибки 2-х родов. Ошибка 1-го рода состоит в том, что будет отвернута правильная нулевая гипотеза. Ошибка 2-го рода состоит в том, что будет принята нулевая гипотеза, в то время как в действительности верна альтернативная гипотеза. Исключить ошибки первого и второго рода невозможно в силу ограниченности выборки. Поэтому стремятся минимизировать потери от этих ошибок. Вероятность совершить ошибку первого рода принято обозначать a (уровень значимости). Вероятность совершить ошибку второго рода обозначают, b. Тогда вероятность не совершить ошибку второго рода (1- b) называется мощностью критерия. Для проверки статистической гипотеза используют специально подобранную СВ (статистику, критерий), точное или приближенное значение которой известно.Эту величину обозначают: U (или Z) – если она имеет стандартизированное нормальное распределение; T - если она распределена по закону Стьюдента; c2 - если она распределена по закону c2; F – если она имеет распределение Фишера. Для общности такую СВ будут обозначать через К. Статистическим критерием называют СВ К, которая служит для проверки нулевой гипотезы. После выбора определенного критерия множество всех его возможных значений разбивают на два непересекающихся подмножества. Совокупность значений критерия, при которых нулевая гипотеза отклоняется, и другое - при которых она не отклоняется.
Первое подмножество называют критической областью, второе - областью принятия гипотезы. Точки, разделяющие эти области, называют критическими. Проверка значимости (статистической) уравнения регрессии означает проверку соответствия модели, выражающей зависимость между переменными, экспериментальным данным, а также проверку достаточности включенных в уравнение объясняющих переменных для описания зависимой переменной. Правило проверки статистической значимости оценок a, b основывается на статистических свойствах оценок МНК и проверке статист. гипотез H0 H1. Невозможность отклонения какой-либо из гипотез означает статистическую незначимость соответствующего коэффициента и наоборот, отклонение какой-либо из гипотез означает, что соответствующий коэффициент статистически значим. Как всегда, проверка статистических гипотез осуществляется при некотором уровне значимости. В практических эконометрических исследованиях наиболее часто используются 5% и 1% уровни значимости. Выбор того или иного уровня значимости определяется исследователем. Напомним, что если нулевая гипотеза отклоняется при 1%-ном уровне значимости, то она автоматически отклоняется и при 5%-ном уровне. Если нулевая гипотеза принимается при 5%-ном уровне значимости, то она принимается и при 1%-ном уровне. Если же при 5%-ном уровне значимости нулевая гипотеза отклоняется, то необходимо проверить ее при 1%-ном уровне и, если при этом уровне она принимается, то результаты проверки гипотезы приводятся для двух уровней значимости. 46. Эффективность параметра регрессии а1, полученного МНК и полученного по крайним точкам Эффективность по МНК: Свойство эффективности оценок неизвестных параметров модели регрессии, полученных методом наименьших квадратов, доказывается с помощью теоремы Гаусса-Маркова. Сделаем следующие предположения о модели парной регрессии: 1) факторная переменная xi – неслучайная или детерминированная величина, кᴏᴛᴏᴩая не зависит от распределения случайной ошибки модели регрессии βi;
2) математическое ожидание случайной ошибки модели регрессии равно нулю во всех наблюдениях:
3) дисперсия случайной ошибки модели регрессии постоянна для всех наблюдений:;
4) между значениями случайных ошибок модели регрессии в любых двух наблюдениях отсутствует систематическая взаимосвязь, т. е. случайные ошибки модели регрессии не коррелированны между собой (ковариация случайных ошибок любых двух разных наблюдений равна нулю):
Это условие выполняется в том случае, если исходные данные не будут временными рядами; 5) на основании третьего и четвёртого условий часто добавляется пятое условие, заключающееся в том, что случайная ошибка модели регрессии – ϶ᴛᴏ случайная величина, подчиняющейся нормальному закону распределения с нулевым математическим ожиданием и дисперсией G2: εi~N(0, G2). В случае если выдвинутые предположения справедливы, то оценки неизвестных параметров модели парной регрессии, полученные методом наименьших квадратов, имеют наименьшую дисперсию в классе всех линейных несмещённых оценок, т. е. МНК-оценки можно считать эффективными оценками неизвестных параметров β0 и β1. В случае если выдвинутые предположения справедливы для модели множественной регрессии, то оценки неизвестных параметров данной модели регрессии, полученные методом наименьших квадратов, имеют наименьшую дисперсию в классе всех линейных несмещённых оценок, т. е. МНК-оценки можно считать эффективными оценками неизвестных параметров β0…βn. 47. Расчет параметров множественной линейной регрессии МНК. Формулы расчетов Предположим, что переменная Y есть линейная функция X, с неизвестными параметрами b1 and b2, оценка которых есть основная задача регрессионного анализа, а также имеется выборка из 4-х наблюдений X, значения которой известны. На практике большинство экономических зависимостей (Рi) не являются точными и действительное значение Y будет отличаться от теоретического. Каждое значение Y включает неслучайную объясняющую компоненту b1 + b2X, и компоненту случайного возмущения u. На практике можно видеть только Pi точки. Их можно использовать для аппроксимации линии Y = b1 + b2X. Эта аппроксимация обозначается как ŷ = b1 + b2X, где b1 - это оценка b1, а b2 – это оценка b2. Оцененная регрессионная прямая Используя теоретическую модель, Y можно представить в виде неслучайной компоненты b1 + b2X и случайной компоненты u. На практике значения b1 и b2 неизвестны и, следовательно неизвестны значения случайного возмущения. Для оцененной прямой в каждом наблюдении можно определить оценку и остаток, которые используются для прогноза. Для исходной парной линейной эконометрической модели, представленной в виде у=а0+а1х+ut необходимо построить парную линейную регрессию вида Построение линейной регрессии
и постоянный коэффициент
48. Оценка параметров нелинейной модели и запись полученной регрессии. Для учета влияния нескольких факторов, воздействующих на объект исследования используется множественная регрессия: yi = a0 + a1· xi1 + a2· xi2 + … + aj · xij +… + am· xim + εi, где i = 1,2,…,n – номер наблюдения, j = 1,2,…,m – номер фактора, yi – значение признака-результата, xij – значение j - го фактора для i –го наблюдения, εi – случайная составляющая, a0 – свободный член, показывает среднее значение yi при x1 = x2 =… xm = 0, aj – коэффициент регрессии при j – ом факторе, характеризует среднее изменение признака-результата y с изменением xj на одну единицу, при условии, что прочие факторы не изменяются. Уравнение множественной регрессии в матричной форме: Y = X·A + ε, где Y – вектор-столбец (nx1) зависимой переменной; X – матрица nx(m+1) независимых переменных значений факторов; A – вектор-столбец (m+1)x1 неизвестных коэффициентов регрессии; ε – вектор-столбец (nx1) случайных отклонений. Параметры системы нормальных уравнений находятся с помощью МНК по формуле: a = (XT · X)-1· XT · Y. где a – вектор параметров К факторам, включаемым в модель регрессии предъявляются следующие требования: · Должны иметь количественную оценку; · Должна быть тесная связь каждого фактора с результатом; · Не должны сильно коррелировать между собой.
49. Двухшаговый метод наименьших квадратов для оценки параметров структурной формы модели. Модель Сверхидентифицируема, если число приведенных коэффициентов больше числа структурных коэффициентов. В этом случае на основе коэффициентов приведенной формы можно получить два или более значений одного структурного коэффициента. Если система сверхидентифицируема, то КМНК не используется, ибо он не дает однозначных оценок для параметров структурной модели. В этом случае могут использоваться разные методы оценивания, среди которых наиболее распространенным и простым является двухшаговый метод наименьших квадратов (ДМНК).
Суть ДМНК заключается в следующем: Шаг 1. Обычным методом наименьших квадратов оценивается зависимость эндогенных переменных от всех экзогенных (фактически оценивается неограниченная приведённая форма). Шаг 2. Обычным методом наименьших квадратов оценивается структурная форма модели, где вместо эндогенных переменных используются их оценки, полученные на первом шаге При точной идентифицируемости системы ДМНК-оценки совпадают с КМНК-оценками. Можно показать, что ДМНК-оценки параметров каждого уравнения фактически равны:
Как видно из описания данного алгоритма, традиционный МНК применяется два раза (для определения оценок эндогенных переменных приведённой формы и для определения оценок структурных параметров уравнений системы), поэтому и получил название двухшагового. 50. Косвенный метод наименьших квадратов для оценки параметров структурной формы модели. Метод решения точно идентифицируемой системы уравнений (то есть все структурные коэффициенты определяются однозначно (единственным способом) по коэффициентам приведенной формы модели. И число параметров структурной модели равно числу параметров приведенной формы называется косвенным методом наименьших квадратов (КМНК), так как МНК применяется не прямо к структурным уравнениям, а к приведенным. Полученные значения параметров приведенных уравнений зависят только от входящих в приведенные уравнения экзогенных переменных и не содержат искажающего влияния других факторов на вариацию эндогенных переменных. При алгебраическом преобразовании параметров приведенных уравнений в параметры структурных уровней, естественно, никакие посторонние факторы на результат не влияют. Следовательно, при КМНК мы получим неискаженные, т.е. состоятельные и несмещенные, значения параметров структурных уравнений. Алгоритм КМНК включает 3 шага: 1) составление приведенной формы модели и выражение каждого коэффициента приведенной формы через структурные параметры; 2) применение обычного МНК к каждому уравнению приведенной формы и получение численных оценок приведенных параметров; 3) определение оценок параметров структурной формы по оценкам приведенных коэффициентов, используя соотношения, найденные на шаге 1. 51. Замещающие переменные. Причины и условия их применения. Требования к данным переменным. Переменные, которые вводятся в эконометрические модели вместо тех переменных, которые не поддаются измерению, называются замещающими. (Некоторые переменные, относящиеся к соц-экономическому положению или качеству образования, имеют расплывчатое определение и их нельзя измерить, другие показатели требуют для своего измерения очень много времени и средств.) Требование. Замещающая переменная должна коррелировать с переменной, которую она замещает. Если Cor(x,xpr)=+-1, то xpr – называют совершенным регрессором
В качестве замещающей переменной часто используется время и лаговые переменные. Имеются 2 причины для поиска замещающей переменной: 1) Если не использовать замещающую переменную, то регрессия может пострадать от смещения оценок и стат проверка будет неполноценной. 2) Результаты оценки регрессии с включением замещающей переменной могут дать косвенную информацию о переменных, которая замещена выбранной переменной. Предположим что истиной моделью явл. Y=a+b1x1+b2x2+…+bkxk+e и допустим, что не имеется данных по существенной переменой х1. Если невкл. В модель эту переменную то регрессия может пострадать от смещения оценок и стат-ая проверка будет некорректной. Если вместо отсутствующей переменной х1 использовать ее заменитьель z линейно связанный с х1, и построить регрессию yˆ=a+b2x2+…+bkxk +cz то оценки b2..bk их стандарт ошибки и коэф-т R2 будут такими же как и с использованием х1. На практике обычно невозможно найти замещающую переменную, имеющую строгую линейную зависимость с недостающей переменной, но если связь близка к линейной, то результат получается приблизительно на том же уровне. Основной проблемой является отсутствие возможности для проверки наличия линейной связи между истинной и замещающей переменной. И часто такая оценка сводится к субъективной оценке. 52. Методы подбора объясняющих переменных множественной эконометрической модели. Свойства, предъявляемые к переменным. Алгоритмы подбора. Множественная регрессия имеет вид: Е[Y/ x1, x2….. xm]=f (x1,x2….xm) Уравнение множественной регрессии: Y=f(β, X)+ ε Где (x1, x2, …, xm)- вектор объясняющих переменных, β -вектор параметров (подлежащих определению), ε – вектор случайных ошибок(отклонений) Y – зависимая переменная С формальной точки зрения, объясняющие переменные в линейной эконометрической модели должны обладать следующими свойствами: • иметь высокую вариабельность; • быть сильно коррелированными с объясняемой переменной; • быть слабо коррелированными между собой; • быть сильно коррелированными с представляемыми ими другими переменными, не используемыми в качестве объясняющих. Объясняющие переменные подбираются с помощью статистических методов. Процедура подбора переменных состоит из следующих этапов: 1. На основе накопленных знаний составляется множество так называемых потенциальных объясняющих переменных (первичных переменных), в которое включаются все важнейшие величины, влияющие на объясняемую переменную. Такие переменные будем обозначать 2. Собирается статистическая информация о реализациях как объясняемой переменной, так и потенциальных объясняющих переменных. Формируется вектор у наблюдаемых значений переменной Y и матрица X наблюдаемых значений переменных
3. Исключаются потенциальные объясняющие переменные, характеризующиеся слишком низким уровнем вариабельности. 4. Рассчитываются коэффициенты корреляции между всеми рассматриваемыми переменными. 5. Множество потенциальных объясняющих переменных редуцируется с помощью выбранной статистической процедуры. Индивидуальные показатели информационной емкости в рамках конкретной комбинации рассчитываются по формуле
Интегральные рассчитываются по формуле
53. Модели с бинарными фиктивными переменными и, в каких случаях они применяются. Термин “фиктивные переменные” используется как противоположность “значащим” переменным, показывающим уровень количественного показателя, принимающего значения из непрерывного интервала. Как правило, фиктивная переменная — это индикаторная переменная, отражающая качественную характеристику. Чаще всего применяются бинарные фиктивные переменные, принимающие два значения: 0 и 1, в зависимости от определенного условия. Например, в результате опроса группы людей 0 может означать, что опрашиваемый - мужчина, а 1 - женщина. Могут быть разного рода атрибутивные признаки, такие, например, как профессия, пол, образование, климатические условия, принадлежность к определенному региону. Заметим, что бинарный характер фиктивных переменных фактически влечет изменение структуры уравнения модели в зависимости от значения этих перем-ых. Такие модели называются моделями с переменной структурой. Кол-во фикт. перем-ых должно быть на 1 меньше числа возможных уравнений качественного фактора. По договорённости о состояние фактора, при котором все фикт.пер-ые равны 0, именуется базовым. К фиктивным переменным иногда относят регрессор, состоящий из одних единиц (т.е. константу, свободный член), также временной тренд. Фиктивные переменные, будучи экзогенными, не создают каких-либо трудностей при применении ОМНК. Фиктивные переменные являются эффективным инструментом построения регрессионных моделей и проверки гипотез. 54. Фиктивные переменные сдвига. Спецификация эконометрической модели. Пример применения фиктивных переменных Фиктивная переменная сдвига – это переменная, которая меняет точку пересечения линии регрессии с осью ординат в случае применения качественной переменной.
Переход фиктивной переменной с одной градации на другую вызывает скачкообразное изменение эндогенной переменной. Фиктивные переменные, которые приводят лишь к скачкообразному изменению эндогенной переменной, называются фиктивными переменными сдвига Фиктивные переменные применяют при построение динамических моделей, когда с определенного момента времени начинает действовать какой-либо качественный признак.
Введение дополнительного слагаемого в спецификацию модели позволяет учесть возможность одновременного сдвига (изменение свободного коэффициента) и наклона (коэффициента при количественном регрессоре) прямой зависимости переменной y от x. Значение фиктивной переменной dt=0 называется базовым, или сравнительным. Выбор базового значения определяется целями исследования или принимается произвольно. При замене базового значения переменной суть модели не меняется, а меняется знак параметра Y на противоположный. Для того, чтобы дать интерпретацию параметру δ, определим условное мат. ожидание зависимой переменной:
Т.о., величина δ -это среднее изменение изучаемого признака при переходе из одной категории в другую при неизменных значениях остальных параметров. Геометрическая интерпретация параметра δ:
55. Фиктивные переменные наклона. Спецификация эконометрической модели. Пример применения фиктивных переменных Фиктивная переменная наклона изменяет наклон линии регрессии. При помощи фиктивных переменных наклона можно построить кусочно-линейные модели, которые позволяют учесть структурные изменения в экономических процессах (например, введение новых правовых или налоговых ограничений, изменение политической ситуации и т. д.). Как правило, фиктивная переменная — это индикаторная переменная, отражающая качественную характеристику. Чаще всего применяются бинарные фиктивные переменные, принимающие два значения, 0 и 1, в зависимости от определенного условия. К фиктивным переменным иногда относят регрессор, состоящий из одних единиц (т.е. константу, свободный член), а также временной тренд. Фиктивные переменные, будучи экзогенными, не создают каких-либо трудностей при применении ОМНК. Фиктивные переменные являются эффективным инструментом построения регрессионных моделей и проверки гипотез.
Фиктивная переменная наклона изменяет наклон линии регрессии. При помощи фиктивных переменных наклона можно построить кусочно-линейные модели, которые позволяют учесть структурные изменения в экономических процессах (например, введение новых правовых или налоговых ограничений, изменение политической ситуации) Спецификация регрессионной модели в этом случае (например, для парной регрессионной модели, для простоты) имеет вид:
0 – до структурных изменений dt = 1 – после структурных изменений, dt - бинарная переменная Фиктивная переменная входит в уравнение в мультипликативной форме. Таким образом, введение в спецификацию модели дополнительного слагаемого в виде произведения количественной и фиктивной переменных позволяет учесть возможность одновременного сдвига (изменение свободного коэффициента) и наклона (коэффициента при количественном регрессоре) прямой зависимости переменной у от х.
Регрессионная модель, включающая в качестве фактора (факторов) фиктивную переменную, называется регрессионной моделью с переменной структурой. Число сезонных фиктивных переменных в регрессионной модели всегда должно быть на единицу меньше сезонов внутри года, т. е. должно быть равно величине L − 1. При моделировании годовых данных регрессионная модель, помимо фактора времени, должна содержать одиннадцать фиктивных компонент (12 − 1).
Каждому из сезонов соответствует определенное сочетание фиктивных переменных. Сезон, для которого значения всех фиктивных переменных равны нулю, принимается за базу сравнения. Для остальных сезонов одна из фиктивных переменных принимает значение, равное единице. Если имеются поквартальные данные, то значения фиктивных переменных D1, D2, D3 будут принимать следующие значения для каждого из кварталов. Тогда общий вид модели регрессии с переменной структурой будет иметь вид: yt=β0+ β1*t+δ2*D2+δ3*D3+δ4*D4+εt. На основе общей модели регрессии с переменной структурой можно составить базисную модель или модель тренда для первого квартала: yt=β0+ β1*t+εt. Также на основе общей модели регрессии с переменной структурой можно составить частные модели регрессии: 1) частная модель регрессии для второго квартала: yt=β0+ β1*t+δ2+εt; 2) частная модель регрессии для третьего квартала: yt=β0+ β1*t+δ3+εt; 3) частная модель регрессии для четвёртого квартала: yt=β0+ β1*t+δ4+εt. Данные частные модели регрессии отличаются друг от друга только на величину свободного члена δi. Коэффициент β1 характеризует среднее абсолютное изменение уровней временного ряда под влиянием основной тенденции. Сезонная компонента для каждого сезона рассчитывается как разность между средним значением свободных членов всех частных моделей регрессий и значением постоянного члена одной из моделей. Среднее значение свободных членов всех частных моделей регрессий рассчитывается по формуле: Для поквартальных данных оценка сезонных отклонений осуществляется по формулам: 1) оценка сезонного отклонения для первого квартала: 2) оценка сезонного отклонения для второго квартала: 3) оценка сезонного отклонения для третьего квартала: 4) оценка сезонного отклонения для четвёртого квартала: Сумма сезонных отклонений должна равняться нулю.
|
|||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-06-14; просмотров: 90; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.100.34 (0.069 с.) |


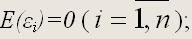



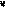



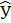 , предсказывающая значения Y (оценки Y). Разница между действительным и оцененным значением Y - это остаток e! Остаток не совпадает со случайной переменной. Случайное возмущение – это разница между неслучайным теоретическим значением и действительным значением. Остаток – это разница между действительным и оцененным значением.
, предсказывающая значения Y (оценки Y). Разница между действительным и оцененным значением Y - это остаток e! Остаток не совпадает со случайной переменной. Случайное возмущение – это разница между неслучайным теоретическим значением и действительным значением. Остаток – это разница между действительным и оцененным значением.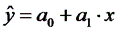
 сводится к оценке ее параметров а0 и а1
сводится к оценке ее параметров а0 и а1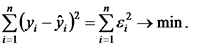
 Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений результативного признака у от оценочного у минимальна, т.е.
Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений результативного признака у от оценочного у минимальна, т.е. Для линейной регрессии параметры и находятся из системы нормальных уравнений:
Для линейной регрессии параметры и находятся из системы нормальных уравнений: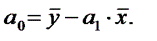 Решая систему, находим оценку коэффициента парной линейной регрессии:
Решая систему, находим оценку коэффициента парной линейной регрессии: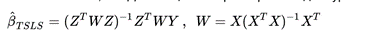 где Z - матрица всех переменных правой части данного уравнения, X - матрица всех экзогенных переменных системы.
где Z - матрица всех переменных правой части данного уравнения, X - матрица всех экзогенных переменных системы.
 в виде
в виде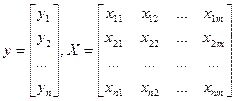
 ; (l=1,2,…,L; j=1,2,…
; (l=1,2,…,L; j=1,2,…  ), где l – номер переменной,
), где l – номер переменной, 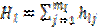 , (l=1,2,…,L). В качестве объясняющих выбирается такая комбинация переменных, которой соответствует максимальное значение интегрального показателя и формационной емкости.
, (l=1,2,…,L). В качестве объясняющих выбирается такая комбинация переменных, которой соответствует максимальное значение интегрального показателя и формационной емкости. — модель с фиктивной переменной сдвига;
— модель с фиктивной переменной сдвига;