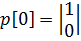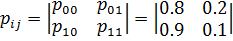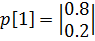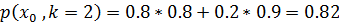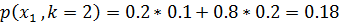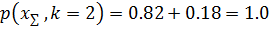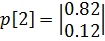Емкость контейнера – 10 изделий

2. Изделия поступают в случайный момент времени, величина которого распределена по закону Пуассона с параметром λ=10 (в среднем 10 минут на изготовление изделия)

 

Создайте новый скрипт. Скопируйте в него программу, приведенную ниже:

x=1:10;

y=1:10;

lambda =6;

for i=1:10

s=0;

for j=1:10

z= poissrnd(lambda);

s=s+z;

end

y(i)=s;

end

plot(x, y)

Запустите скрипт. Проанализируйте график времени заполнения контейнеров. Объясните логику программы.

 

Лабораторная работа №5.

Параметры эмпирического распределения

 

Создадим функцию для генерации эмпирических данных. Генерировать будем из суммы двух распределений: нормального и равномерного, сдвинутого от центра нормального. Для получения индивидуального распределения используем N – номер студента в списке группы.

Будем считать, что сгенерированные данные - это выборка из некоторой генеральной совокупности значений случайной величины.

Откроем окно m – функции:

 

New -> Functiion

 

В окно m функции внесем текст:

 

function x=pdisp(N,K)

for i=1:N

rand;

end

m=N+rand*10;

s=N/3;

x1 = normrnd(m,s,1,K);

a=N-s;

b=N+s*3;

x2 = unifrnd(a,b,1,K);

x=x1+x2;

end

 

Сохраним функцию Save As как pdisp. m

 

Вернемся в командное окно MatLab. Введём последовательно текст по строкам (комментарии можно не вводить):

 

N=input('Номер студента по списку =')

% Число данных

K=500;

%Зарезервируем матрицу-массив для y.

y=zeros(1,K);

% Сгенерируем данные

y=pdisp(N,K);

 

Возможно программа укажет, что функция pdisp находится в другой папке. Щелкните на 1-й фразе сообщения об ошибке (Change the MATLAB current folder). Программа исправит ошибку. Снова введите последнюю команду.

 

% Построим гистограмму

hist(y,10);

 

Рассчитаем статистические параметры случайной величины:

(Не забудьте перебить апострофы!)

 

disp('Оценка математического ожидания ')

M=mean(y)

disp(‘Оценка среднего квадратичного отклонения’)

S=std(y)

disp('% Среднегеометрическое ')

G=geomean(y)

disp('% Медиана распределения ')

ME=median(y)

disp('Первый, Второй, Третий, Четвёртый моменты распределения ')

M1=moment(y,1)

M2=moment(y,2)

M3=moment(y,3)

M4=moment(y,4)

%M1 должно равняться нулю

%Другие коэффициенты

disp('Ассиметрия ')

AS=(M3/S^3)

disp('Аксцесс')

AC=(M4/S^4-3)

 

Проведем статистическую проверку гипотезы методом Ярки-Бера на не противоречие распределения значений случайной величины нормальному закону:

 

H = jbtest(y)

 

Функция возвращает скаляр H, являющийся результатом проверки нулевой гипотезы для критического уровня значимости равного 0,05.

Нулевая гипотеза состоит в том, что распределение генеральной совокупности значений случайной величины не противоречит нормальному закону. Альтернативная гипотеза теста Ярки-Бера состоит в том, что распределение генеральной совокупности противоречит нормальному закону. Нулевая гипотеза принимается если Н=0. Если H =1, то нулевая гипотеза может быть отвергнута.

 

Лабораторная работа №6.

Марковские процессы

 

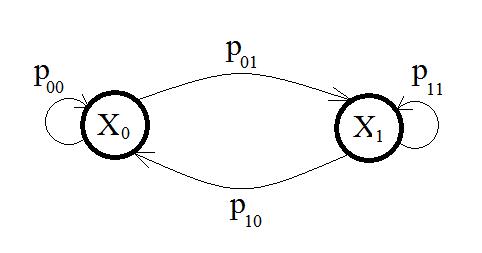
Случайный Марковский процесс (Цепи Маркова) назван в честь русского математика Маркова А.А. (1856-1922). Работы Маркова А.А. стали известны широкому кругу математиков (в т.ч. за рубежом) благодаря книге академика Колмогорова А.Н. (1936 г.).

Случайный процесс называется Марковским в том случае, если вероятность будущего состояния системы зависит только от его состояния в настоящий момент времени и не зависит от его состояния в прошлом. Марковский процесс является дискретным, если переход из одного состояния в другое совершается скачком (мгновенно).

Рассмотрим Марковский процесс на примере. Пусть имеем техническое устройство, которое может находиться в двух состояниях: исправно (x ₀) и неисправно (x ₁). Для иллюстрации Марковского процесса часто используются графы. Граф — абстрактный математический объект, представляющий собой множество вершин и набор рёбер, соединяющих их. Граф для двух состояний показан на рис.6.

Рис. 6

 

P₀₀ – вероятность того, что система останется в исправном состоянии;

P₀₁ – вероятность того, что система перейдет из исправного состояния в неисправное;

P₁₀ – вероятность того, что система перейдет из неисправного состояния в исправное;

P₁₁ – вероятность того, что система останется в неисправном состоянии.

В начальный момент времени система находится в исправном состоянии:

 

 

Пусть матрица переходов системы из i – го состояния в j – ое составляет:

 

 

После первого шага система перейдет в состояние:

 

 

Поскольку достоверно неизвестно в каком состоянии система после первого шага (k =1), для определения состояния системы на втором шаге надо применить формулу полной вероятности.

Полная вероятность того, что система будет находится в исправном состоянии на шаге k =2 состоит из вероятности исправного состояния на первом шаге умноженная на вероятность, что система останется в исправном состоянии плюс вероятность неисправного состояния на первом шаге, умноженная на вероятность перехода из неисправного состояния в исправное:

 

 

 

Вероятность противоположного события:

 

 

 

 

Суммарная вероятность:

 

 

Что и следовало ожидать.

Вектор состояния системы на втором шаге: