
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Нормальный закон распределения
Параметрами нормального закона распределения являются математическое ожидание M и D дисперсия. Дисперсия имеет размерность квадрата случайной величины, поэтому удобнее пользоваться другой величиной – среднеквадратическим отклонением:
σ =
Функция normrnd(M,SIGMA, m, n) предназначена для генерации матрицы m x n псевдослучайных чисел по нормальному закону для M (математического ожидания) и SIGMA (среднеквадратического отклонения). Скалярный параметр n задает длину выборки. Зададим 100 значений параметра x (вектор 1 х 100), имеющим нормальный закон распределения с математическим ожиданием M =0 и среднеквадратическим отклонением σ =1
y=normrnd(0, 1, 1, 100);
Для построения гистограммы по сгенерированным данным расcчитаем центры 20 интервалов в диапазоне от -3 до 3:
x=zeros(1, 20); d=(3-(-3))/38;
Ширина интервала 2* d.
for i=1:20 x(i)=-3+ 2*d*(i-1); end
Построим гистограмму значений y, попавших в интервалы x.
hist(y, x)
Запомним значения гистограммы
y1=hist(y, x);
y 1 - высота столбцов гистограммы. Значения графика плотности эмпирического закона определим из условия (площади под графиком эмпирической плотности распределения должна равняться 1):
Тогда
y11=y1./ (2*d*100);
Посчитаем теоретические значения нормального закона распределения для значений x:
y0=normpdf(x, 0, 1);
Сравним графики теоретического и экспериментального законов плотности распределения:
plot(x, y11,'-g', x, y0, '-r')
Определим среднее значение для эмпирического распределения:
m=sum(x.*y1)/100
Математическое ожидание теоретического распределения равно нулю. Неувязка указывает на недостаточное количество сгенерированных данных.
Среднеквадратическое отклонение:
sx=0 for i=1:20 sx= sx+(m-x(i))^2*y1(i); end sigma= sqrt(sx/100)
Теоретическое значение среднеквадратического отклонения 1.
Рассмотрим три закона нормального распределения с математическими ожиданиями -2, 0, 2 и среднеквадратичным отклонением, равным 1.
Создадим массив для данных:
z1=zeros(1,100); z2=zeros(1,100); z3=zeros(1,100); w1=zeros(1,11); w2=zeros(1,11); w3=zeros(1,11);
Заполним массивы случайными числами, распределенными по нормальному закону:
z1=normrnd(-2, 1, 1, 100); z2= normrnd(0, 1, 1, 100); z3= normrnd(2, 1, 1, 100);
Найдем центры интервалов для каждого распределения:
t1=-5:0.6:1; t2=-3:0.6:3; t3=-1:0.6:5;
Шаг d=0.6. Построим гистограммы распределений:
hist(z1,t1) hist(z2,t2) hist(z3,t3)
Запомним значения столбцов гистограммы:
w1=hist(z1,t1); w2=hist(z2,t2); w3=hist(z3,t3);
Нормализируем эмпирические плотности распределений:
d=0.6 w11=w1./ (2*d*100); w22=w2./ (2*d*100); w33=w3./ (2*d*100);
Построим графики:
plot(t1,w11, '-g',t2,w22, '-r',t3,w33, '-b')
Рассчитаем средние значения распределений:
m1=sum(t1.*w1)/100 m2=sum(t2.*w2)/100 m3=sum(t3.*w3)/100
Теоретические значения математических ожиданий -2, 0, 2. Рассчитаем среднеквадратичные отклонения:
sx1=0; sx2=0; sx3=0; for i=1:11 sx1= sx1+(m1-t1(i))^2*w1(i); sx2= sx1+(m2-t2(i))^2*w2(i); sx3= sx3+(m3-t3(i))^2*w3(i); end
sigma1= sqrt(sx1/100) sigma2= sqrt(sx2/100) sigma3= sqrt(sx3/100)
Как и в прошлый раз, теоретическое значение во всех трех случаях равно1.
Для дальнейшего анализа объединим все три распределения:
q=zeros(1,300); for i=1:100 q(i)=z1(i); q(i+100)=z2(i); q(i+200)=z3(i); end
Массив интервалов:
p=zeros(1, 20);
Шаг интервала:
d=(5-(-5))/38;
Ширина интервала 2*d:
for i=1:20 p(i)=-5+ 2*d*(i-1); end
Гистограмма распределения:
hist(q, p)
Запомним значения столбцов:
s1=hist(q,p);
s1 - высота столбцов.
Определим координаты эмпирического графика плотности распределения
s11=s1./ (2*d*300);
Значение математического ожидания распределения равно 0. Теоретическое среднеквадратичное отклонение найдем исходя из того, что в диапазон (-5, +5) укладывается 6 σ (±3).
σ=10/6=1.667
Теоретические значения графика нормального закона распределения:
s0=normpdf(p, 0, 1.667);
Сравним графики теоретического и экспериментального законов плотности распределения:
plot(p,s11,'-g', p, s0, '-r')
Определим среднее значение для эмпирического распределения:
mm=sum(p.*s1)/300
Теоретическое значение математического ожидания 0. Среднеквадратическое отклонение:
sxx=0; for i=1:20 sxx= sxx+(mm-p(i))^2*s1(i); end sigmas= sqrt(sxx/300)
Теоретическое значение 1.667.
|
|||||
|
Последнее изменение этой страницы: 2021-05-11; просмотров: 111; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.213.126 (0.017 с.) |
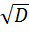
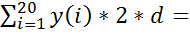 1
1


