
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгоритм решения системы линейных уравнений методом ГауссаСтр 1 из 24Следующая ⇒
Алгебра матриц Матрицей размера
Если Верхнетреугольная матрица – квадратная матрица, у которой все элементы, находящиеся ниже главной диагонали равны 0. Единичная матрица
Операции над матрицами Сложение матриц. Суммой двух матриц A и B размерами
Умножение матрицы на число. Умножением матрицы A на число
Транспонирование. Транспонированием матрицы A называется матрица
Умножение матриц. Умножением матриц A и B размерами
Свойства операций. 1. 2. Для каждой нулевой матрицы размера 3. 4. 5. 6. Если существует результат произведения 7. Если A и B квадратные, тогда 8. 9. 10.
Определитель матрицы Минора Алгебраическим дополнением к элементу
Определитель матрицы (детерминант) – скалярная величина, которая может быть вычислена и поставлена в однозначное соответствие любой квадратной матрице. Определитель матрицы A обозначается как
Данная формула является разложением матрицы A по первой строке. Определитель можно находить по формуле аналогичной, указанной формуле, раскладывая по любой строке или столбцу. Определитель матрицы A размером 2x2 называется число
Определитель матрицы A размером 3x3 называется число
Формулы для случаев 2x2 и 3x3 считают тоже число, что и общая формула для нахождения определителя.
Теорема: Определитель верхнетреугольной матрицы равен произведению элементов главной диагонали. Свойства определителя 1. 2. Если у матрицы поменять местами две строки, то определитель поменяет знак. 3. Если в матрице есть строка или столбец из нулей, то ее определитель равен нулю. 4. Если у матрицы две одинаковые строки или два одинаковых столбца, то ее определитель равен нулю. 5. Общий множитель строки или столбца можно выносить за знак определителя. 6. Если к строке матрицы прибавить или вычесть другую строку, помноженную на любое число, то определитель не изменится. 7.
Обратные матрицы Пусть задана квадратная матрица Если Если A – невырожденная матрица, тогда у нее существует обратная матрица
В данной формуле
Системы линейных уравнений Системой из m линейных уравнений с n неизвестными называется система вида
В данном соотношении Матрица, составленная из коэффициентов при неизвестных, называется матрицей системы. При добавлении в матрицу системы свободные коэффициенты будет получена расширенная матрица системы. Набор из n чисел
Метод Крамера Теорема: Если у системы из n линейных уравнений с n неизвестными матрица системы невырожденная, тогда у системы существует единственное решение, которое можно найти следующим образом
В данной формуле
Матричный метод Если ввести столбец неизвестных
Равносильно системе уравнений
В случае, когда m=n и A – невырожденная матрица, тогда решение системы в матричном виде прите вид
Метод Гаусса Элементарными называются преобразования матрицы 1. Поменять местами две строки. 2. Умножить строку на число, отличное от 0. 3. Прибавить или вычесть из строки другую строку, умноженную на любое число. Элементарные преобразования расширенной матрицы системы приводят к эквивалентной системе, у которой остаются те же решения. Элементарные преобразования относятся только к строчкам матрицы. Ступенчатая матрица – матрица, у которой все ненулевые строки располагаются над всеми чисто нулевыми строками и ведущий элемент каждой ненулевой строки располагается строго правее ведущего элемента в строке, расположенной выше данной. Верхнетреугольная матрица – частный случай ступенчатой матрицы. Алгоритм приведения матрицы к ступенчатому виду с помощью элементарных преобразований 1. Ставим на место первой строки строчку, начинающуюся не с 0. 2. С помощью первой строки обнулим все элементы первого столбца. 3. Повторяем действия 1 и 2 для каждой последующей строки и столбца без учета уже нулевых столбцов и использованных строк. Ранг матрицы Минора, порожденная матрицей Рангом матрицы A ( Теорема Кронеккера-Карелли: Если ранг матрицы системы равен рангу расширенной матрицы системы, тогда система совместна. Если у совместной системы ранг матрицы равен числу неизвестных, тогда решение будет единственным. Если ранг матрицы A меньше числа переменных n, тогда решений системы бесконечно много и для их записи потребуется
Векторная алгебра Вектором называется направленный отрезок. Примеры векторов и их наименований представлены на рисунке 1.
Рисунок 1. Примеры векторов. Вектор не зависит от точки приложения. Нулевой вектор – вектор нулевой длины. Два вектора являются коллинеарными, если они параллельны. Три вектора и более являются компланарными, если они все параллельны некоторой плоскости.
Направляющие косинусы Пусть
Вектор с координатами из направляющих косинусов – отнормированный вектор
Аналитическая геометрия Прямая на плоскости Уравнение с угловым коэффициентом
Рисунок 5. Прямая, заданная уравнением с угловым коэффициентом. Вертикальная прямая имеет уравнение Прямая, проходящая через точку
Рисунок 6. Прямая, проходящая через заданную точку и вектор нормали. Для построения такого вида прямых задается дополнительная точка
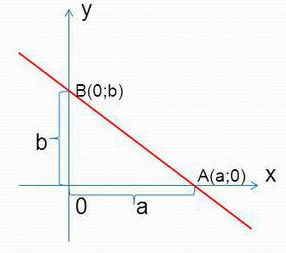
Преобразовав уравнение прямой, проходящей через точку и вектор нормали, можно получить общее уравнение прямой вида Преобразовав уже общее уравнение прямой, будет получено уравнение в прямой в отрезках вида
Построение прямой такого вида представлено на рисунке 7.
Рисунок 7. Построение прямой, заданном в уравнении в отрезках. Дальнейший анализ возможности задать прямую на плоскости приведет еще к двум видам уравнений. Первым из них является параметрическое уравнение прямой, проходящей через точку
Из полученного уравнения вытекает каноническое уравнение прямой
Построение прямой по последним двум последним уравнениям представлены на рисунке 8.
Рисунок 8. Построение прямой, заданной точкой и направляющим вектором. Помимо всех вышеуказанных способов существует еще способ задания прямой с помощью двух точек
Пример прямой такого вида представлен на рисунке 9.
Рисунок 9. Прямая, заданная с помощью двух точек. Помимо способов задания прямой на плоскости, следует определить признаки взаимного расположения прямых на плоскости. Если прямые заданы уравнением с угловым коэффициентом, тогда тангенс угла между заданными прямыми
Исходя из этого уравнения, выделены признаки взаимного расположения прямых: при
Рассматривая общие уравнения прямых, которые имеют вид
Аналогично предыдущему случаю, из этого уравнения вытекают признаки параллельности прямых, если Используя общее уравнение прямой
Расстоянием считается минимальный отрезок (перпендикуляр) от заданной точки до указанной прямой.
Плоскость в пространстве Пусть задана точка
Построение такого вида плоскости представлено на рисунке 10. Для построения выбирается произвольная точка
Рисунок 10. Плоскость, заданная с помощью точки и вектора нормали. Преобразовав предыдущее уравнение можно получить общее уравнение плоскости
Если Дальнейшее преобразования общего уравнения плоскости при условии
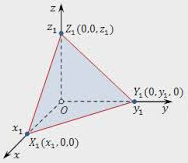
В данном уравнении a, b и c – точки пересечения с соответствующими осями координат и не равны нулю. Построение плоскости такого вида представлено на рисунке 11.
Рисунок 11. Плоскость, заданная с помощью уравнения в отрезках. Помимо вышеуказанных способов задания плоскости в пространстве, также плоскость можно задать с помощью трех точек в пространстве
Рисунок 12. Плоскость, заданная с помощью трех точек. Способ построения подразумевает введения четвертой точки
Помимо рассмотренных способов задания плоскости в пространстве, важным также является анализ взаимного расположения плоскостей в пространстве. Пусть заданы две плоскости в пространстве
Исходя из данного уравнения признаки расположения плоскостей в пространстве будут иметь вид: Если задана плоскость
Прямая в пространстве Поскольку пересечение двух плоскостей в пространстве задают прямую, тогда данная прямая в пространстве описывается системой общих уравнений пересекающихся плоскостей
Построение прямой, указанным способом представлено на рисунке 13.
Рисунок 13. Прямая, заданная пересечением двух плоскостей.
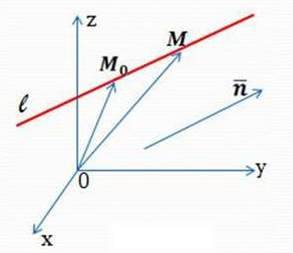
Вторым способом задания прямой в пространстве является задание прямой с помощью точки
Построение прямой с помощью точки и направляющего вектора представлено на рисунке 14.
Рисунок 14. Задание прямой с помощью точки и направляющего вектора. Преобразовав данное уравнение, получим каноническое уравнение прямой в пространстве
Последний рассматриваемый способ построения прямой в пространстве подразумевает введение второй точки
Проанализируем признаки взаимного расположения прямых в пространстве. Пусть заданы две прямые
Исходя из этого уравнения, прямые параллельны, если
Кривые второго порядка Кривой второго порядка называется линия, которая задается уравнением второго порядка вида
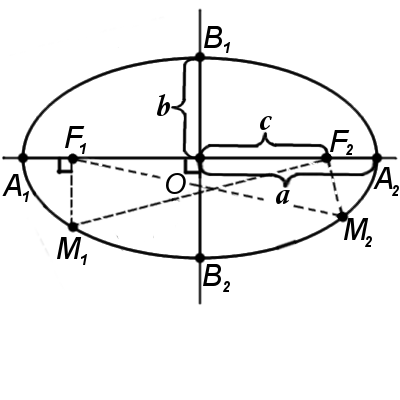
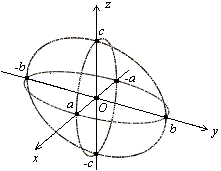
В данном уравнении A, B и C – не равны нулю одновременно. С помощью рассматриваемого уравнения могут быть заданы кривые следующих типов (случаи 4 – 7 называются вырожденными): 1. Эллипс; 2. Гипербола; 3. Парабола; 4. Мнимый эллипс 5. Пара пересекающихся прямых 6. Пара параллельных прямых 7. Точка Эллипс Пусть даны две точки
Рисунок 15. Изображение эллипса. Рассмотрим эллипс на координатной плоскости так чтобы его фокусы были симметричны относительно Oy и лежали на оси Ox (рисунок 16).
Рисунок 16. Расположение эллипса на координатной плоскости. Пусть
Таким образом получим соотношение
Преобразовав полученное соотношение, получим простейшее уравнение эллипса
В полученном уравнении a и b – большие и малые полуоси соответственно. При
Если центр эллипса находится в произвольной точке
Уравнение окружности со смещенным центром, в таком случае, примет вид
Гипербола Зафиксируем две точки Обозначим
Исходя из этого, получим соотношение
Из полученного соотношения получим простейшее уравнение гиперболы
Пример гиперболы представлен на рисунке 17.
Рисунок 17. Изображение гиперболы. Исследовав полученное уравнение гиперболы, получим асимптотические прямые вида
Рисунок 18. Гипербола относительно асимптотических прямых. Прямоугольник с вершинами Если фокусы гиперболы расположить симметрично относительно Oy, тогда ее уравнение примет вид
Если центр гиперболы сместить в точку
Парабола Зафиксируем точку
Рисунок 19. Изображение параболы. При таких условиях парабола пройдет через начало координат. Уравнение такого вида параболы имеет вид
Если Если вершину параболы сместить в точку
Пример параболы со смещенным центром представлен на рисунке 20.
Рисунок 20. Изображение параболы со смещенным центром.
Поверхности второго порядка Пусть на плоскости xOy задана некоторая кривая k с уравнением Если образующая k является кривой второго порядка, тогда соответствующий цилиндр – цилиндр второго порядка. Аналогично можно расположить цилиндр параллельно Ox или Oy, уравнения которых будут содержать y и z или x и z соответственно. Рассмотрим основные типы цилиндров, которые основываются на рассмотренных в трех предыдущих разделах кривых второго порядка. Для удобства все цилиндры расположены параллельно Oz. Первым случаем является эллиптический цилиндр, который имеет уравнение
Пример эллиптического цилиндра представлен на рисунке 21.
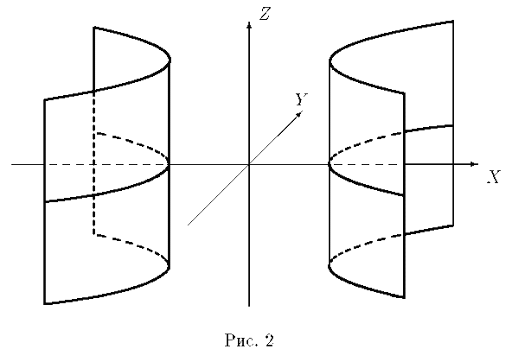
Рисунок 21. Эллиптический цилиндр. Вторым случаем является гиперболический цилиндр, который имеет уравнение
Пример гиперболического цилиндра представлен на рисунке 22.
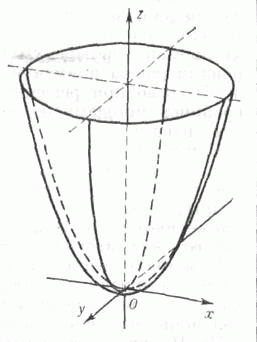
Рисунок 22. Гиперболический цилиндр. Последним случаем является параболический цилиндр, который имеет уравнение
Пример параболического цилиндра представлен на рисунке 23.
Рисунок 23. Параболический цилиндр. Случаи, когда образующая цилиндра имеет смещенный центр в своей плоскости, строятся аналогично рассмотренным выше, с учетом смещения центра образующей кривой.
Поверхности вращения Поверхностью второго порядка называется поверхность, которая задается уравнением второго порядка относительно переменных x, y и z следующего вида
В данном уравнении коэффициенты A, B, C, D, E и F не равны нулю. Рассмотренные в предыдущем разделе цилиндры второго порядка – пример поверхности второго порядка. Помимо цилиндров можно задавать поверхности второго порядка с помощью вращения кривых второго порядка. Основными случаями таких поверхностей являются: · Эллипсоид вращения, имеющий уравнение
Пример эллипсоида вращения представлен на рисунке 24.
Рисунок 24. Эллипсоид вращения. · Конус, имеющий уравнение
Пример конуса представлен на рисунке 25.
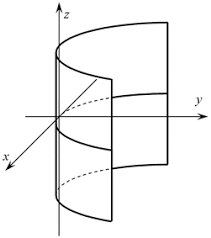
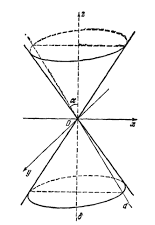
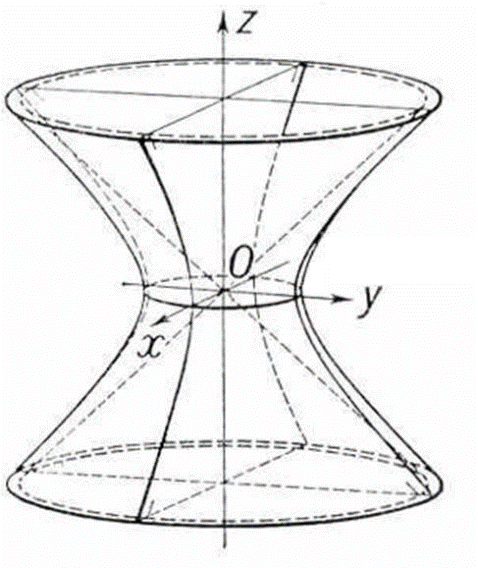
Рисунок 25. Конус. · Однополосный гиперболоид, имеющий уравнение
Пример однополосного гиперболоида представлен на рисунке 26.
Рисунок 26. Однополосный гиперболоид. · Двуполостный гиперболоид, имеющий уравнение
Пример двуполостного гиперболоида представлен на рисунке 27.
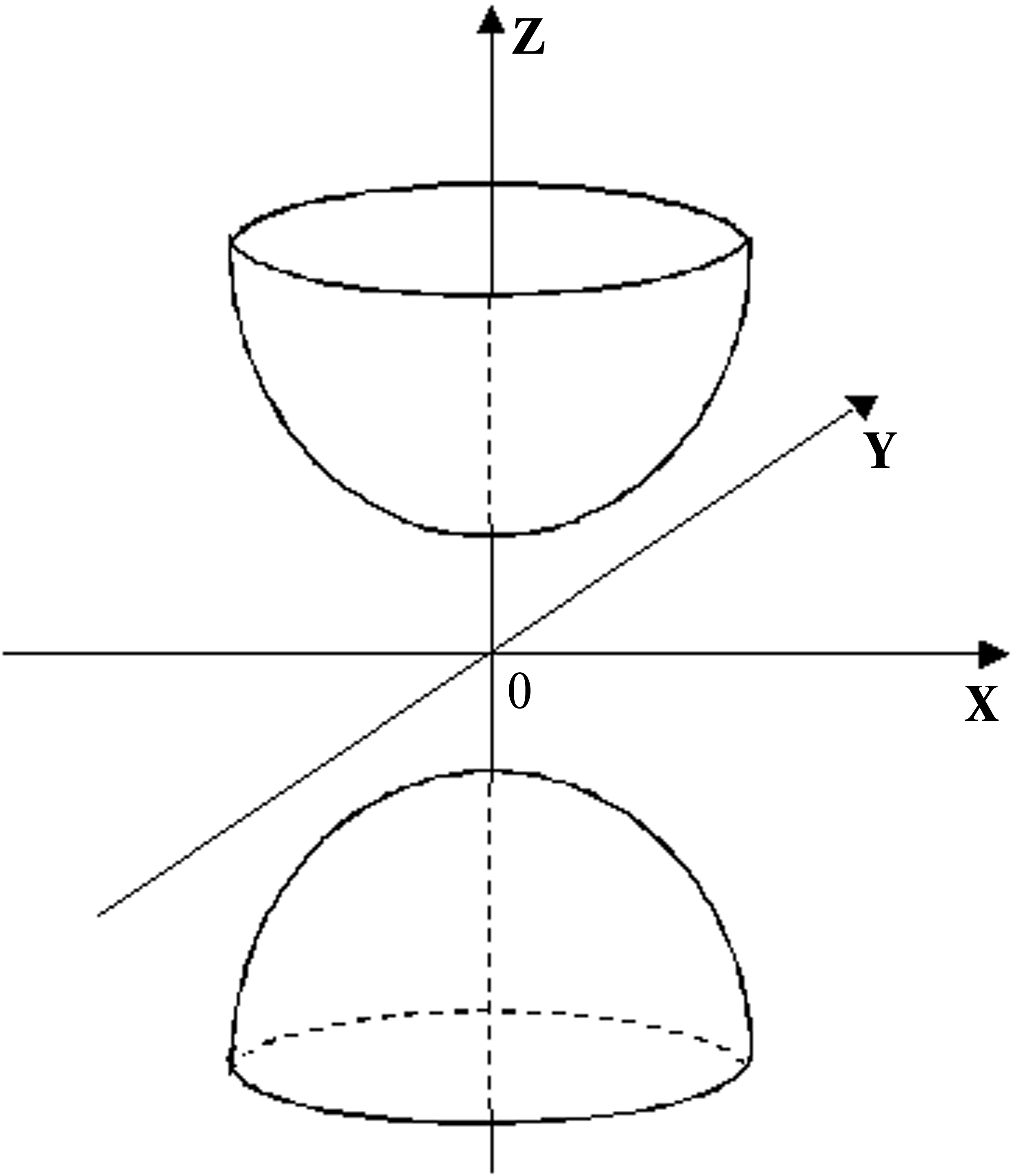
Рисунок 27. Двуполостный гиперболоид. · Эллиптический параболоид, имеющий уравнение
Пример эллиптического параболоида представлен на рисунке 28.
Рисунок 28. Эллиптический параболоид. · Гиперболический параболоид, имеющий уравнение
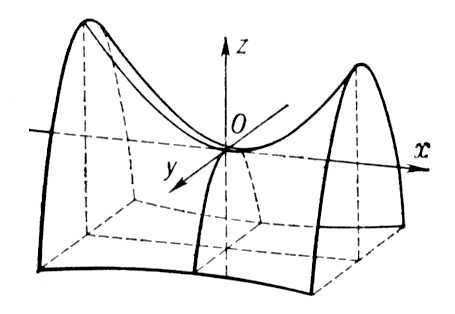
Пример гиперболического параболоида представлен на рисунке 29.
Рисунок 29. Гиперболический параболоид. Гиперболический параболоид не относится к поверхностям вращения и приведен в качестве примера поверхности второго порядка, выпадающей из классификации.
Числа и множества Множества и действия с ними Множество относится к неопределяемым понятиям. Множество задается своими элементами одной или различной природы. Множество при его описании задается перечислением его элементов в фигурных скобках. В других случаях, в фигурных скобках задается правило составления элементов или их общие признаки
Множество, не имеющие элементов, называют пустым множеством Над множествами можно проводить следующие действия: 1. Сравнение Если все элементы множества A принадлежат множеству B, тогда A – подмножество B
Если при этом
2. Объединение – множество 3. Пересечение – множество 4. Дополнение – множество 5. Разность – множество Указанные операции над множествами обладают следующими свойствами: 1. 2. 3. 4. 5. 6. 7. 8. 9.
Множества чисел Кроме рассмотренных выше конечных множеств можно встретить и бесконечные множества, которые бывают двух основных видов:
|
|||||||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 116; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.23.127.197 (0.266 с.) |
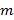 x
x 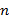 называется таблица их m строк и n столбцов.
называется таблица их m строк и n столбцов.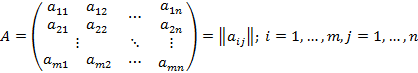
 , тогда матрица называется квадратной, в ее элементы
, тогда матрица называется квадратной, в ее элементы 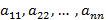 – главной диагональю. Вторая диагональ называется побочной.
– главной диагональю. Вторая диагональ называется побочной.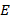 – квадратная матрица, у которой все элементы главной диагонали равны 1, а остальные равны 0.
– квадратная матрица, у которой все элементы главной диагонали равны 1, а остальные равны 0.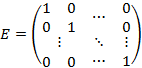
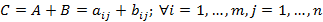
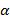 называется матрица C, у которой все элементы равны результату произведения элементов матрицы A на число
называется матрица C, у которой все элементы равны результату произведения элементов матрицы A на число 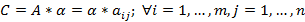
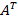 , которая получена преобразованием всех строк в столбцы с тем же номером
, которая получена преобразованием всех строк в столбцы с тем же номером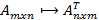
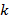 соответственно называется матрица C, у которой все элементы равны соотношению
соответственно называется матрица C, у которой все элементы равны соотношению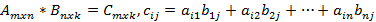
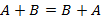 .
.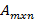
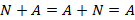 , где N – нулевая матрица (все элементы равны 0).
, где N – нулевая матрица (все элементы равны 0).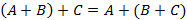 .
.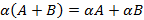 .
.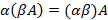 , где
, где 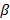 – числа.
– числа.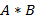 , тогда не всегда существует
, тогда не всегда существует 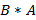 .
.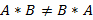 .
.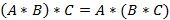 .
.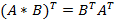 .
.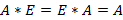 .
.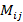 квадратной матрицы A называется определитель матрицы, которая получается из матрицы A удалением i-ой строки и j-столбца.
квадратной матрицы A называется определитель матрицы, которая получается из матрицы A удалением i-ой строки и j-столбца.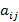 матрицы A называется число
матрицы A называется число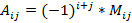
 ,
,  или
или 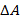 .
.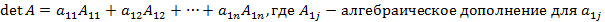
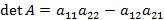
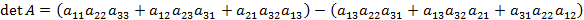
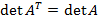 .
.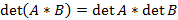 .
.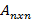 , тогда матрица
, тогда матрица 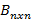 называется обратной, если выполняется равенство
называется обратной, если выполняется равенство 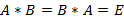 . Если A и B являются обратными матрицами, тогда
. Если A и B являются обратными матрицами, тогда 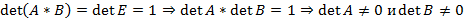 , таким образом, обратная матрица существует, только если у исходной матрицы
, таким образом, обратная матрица существует, только если у исходной матрицы 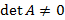 .
.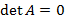 , тогда матрица A называется вырожденной.
, тогда матрица A называется вырожденной.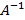 , которую можно найти по формуле
, которую можно найти по формуле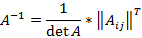
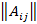 – матрица из алгебраических дополнений (присоединенная матрица) для элементов матрицы A.
– матрица из алгебраических дополнений (присоединенная матрица) для элементов матрицы A.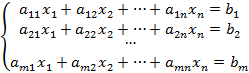
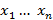 – неизвестные,
– неизвестные, 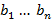 – свободные коэффициенты.
– свободные коэффициенты. называется решением системы, если при подстановке этих чисел в систему ее уравнения обратятся в верные равенства. Решить систему – найти все возможные значения набора из n чисел
называется решением системы, если при подстановке этих чисел в систему ее уравнения обратятся в верные равенства. Решить систему – найти все возможные значения набора из n чисел 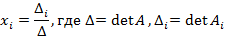
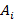 – матрица, полученная из A заменой i-го столбца на столбец свободных коэффициентов b.
– матрица, полученная из A заменой i-го столбца на столбец свободных коэффициентов b.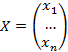 и столбец свободных коэффициентов
и столбец свободных коэффициентов 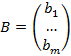 , тогда матричное уравнение
, тогда матричное уравнение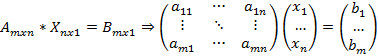
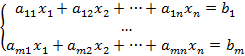
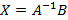
 ) называется наибольший порядок k не нулевого минора, порожденного этой матрицей. Элементарные преобразования не меняют ранг матрицы. Ранг ступенчатой матрицы равен рангу исходной матрицы. Ранг ступенчатой матрицы равен числу ее ненулевых строк.
) называется наибольший порядок k не нулевого минора, порожденного этой матрицей. Элементарные преобразования не меняют ранг матрицы. Ранг ступенчатой матрицы равен рангу исходной матрицы. Ранг ступенчатой матрицы равен числу ее ненулевых строк.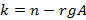 свободных переменных.
свободных переменных.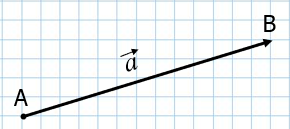
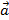 образует с координатными осями Ox, Oy, Oz углы
образует с координатными осями Ox, Oy, Oz углы 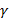 соответственно, тогда
соответственно, тогда  ,
, 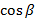 и
и 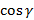 называют направляющими косинусами
называют направляющими косинусами 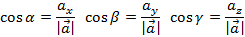
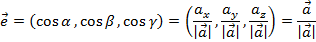
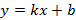 задает все не вертикальные прямые (рисунок 5). В данном уравнении коэффициент
задает все не вертикальные прямые (рисунок 5). В данном уравнении коэффициент 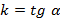 , который влияет на прямую следующим образом:
, который влияет на прямую следующим образом: 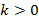 – прямая возрастает,
– прямая возрастает, 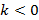 – прямая убывает,
– прямая убывает, 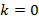 – прямая параллельная оси Ox.
– прямая параллельная оси Ox.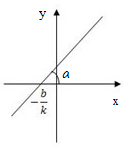
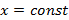 и его невозможно получить из рассматриваемого уравнения.
и его невозможно получить из рассматриваемого уравнения.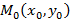 и вектор нормали
и вектор нормали 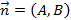 имеет уравнение
имеет уравнение 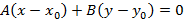 . Построение такого вида прямой представлено на рисунке 6.
. Построение такого вида прямой представлено на рисунке 6.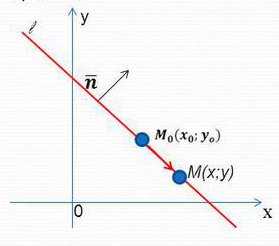
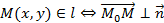 и исходя из координат вектора
и исходя из координат вектора 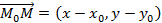 выводится указанное уравнение.
выводится указанное уравнение.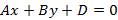 , где A и B – координаты вектора нормали. Полученное уравнение задает все прямые, в том числе и вертикальные прямые.
, где A и B – координаты вектора нормали. Полученное уравнение задает все прямые, в том числе и вертикальные прямые.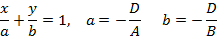
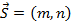
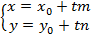
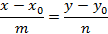
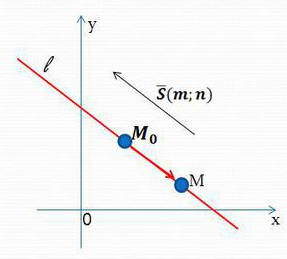
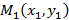

 , имеющими уравнения
, имеющими уравнения 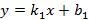 и
и 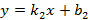 будет равен
будет равен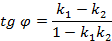
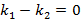 – прямые параллельны и при
– прямые параллельны и при 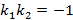 – прямые перпендикулярны.
– прямые перпендикулярны.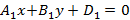 и
и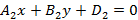 получим косинус угла между прямыми
получим косинус угла между прямыми 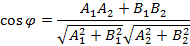
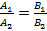 и признак перпендикулярности, если
и признак перпендикулярности, если 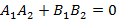 . Угол
. Угол 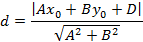
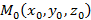 и вектор нормали
и вектор нормали 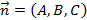 . С их помощью можно найти уравнение плоскости, проходящей через заданную точку и вектор нормали. Данное уравнение имеет вид
. С их помощью можно найти уравнение плоскости, проходящей через заданную точку и вектор нормали. Данное уравнение имеет вид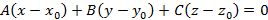
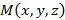 , тогда полученный вектор
, тогда полученный вектор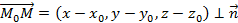 , из которого выводится рассматриваемое уравнение.
, из которого выводится рассматриваемое уравнение.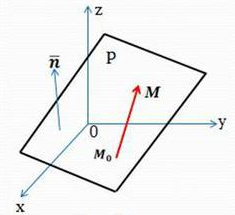
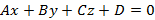
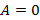 , тогда уравнение плоскости примет вид
, тогда уравнение плоскости примет вид 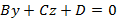 и задает плоскость параллельную Ox. Аналогично, если
и задает плоскость параллельную Ox. Аналогично, если 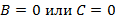 , тогда уравнение плоскости примет вид
, тогда уравнение плоскости примет вид 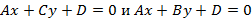 соответственно и задают плоскости параллельные Oy и Oz соответственно. Если
соответственно и задают плоскости параллельные Oy и Oz соответственно. Если 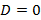 , тогда получим уравнение
, тогда получим уравнение 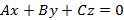 , которая задает плоскость, проходящую через начало координат.
, которая задает плоскость, проходящую через начало координат.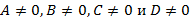 , тогда получим уравнение плоскости в отрезках
, тогда получим уравнение плоскости в отрезках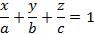
 , которые не лежат на одной прямой. Способ построения плоскости такого вида представлен на рисунке 12.
, которые не лежат на одной прямой. Способ построения плоскости такого вида представлен на рисунке 12.
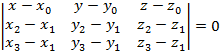
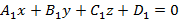 и
и 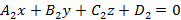 . Если угол между плоскостями равен
. Если угол между плоскостями равен 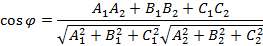
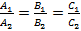 – плоскости параллельны или
– плоскости параллельны или 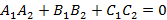 – плоскости перпендикулярны.
– плоскости перпендикулярны.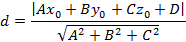
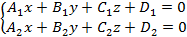
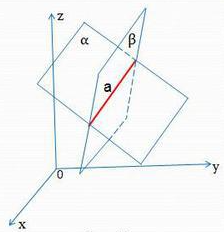
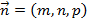 . Из этих данных можно получить параметрическое уравнение прямой в пространстве
. Из этих данных можно получить параметрическое уравнение прямой в пространстве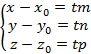
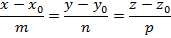
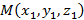 , следовательно возможно получить уравнение прямой в пространстве, проходящей через две заданные точки
, следовательно возможно получить уравнение прямой в пространстве, проходящей через две заданные точки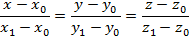
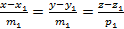 и
и 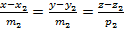 , тогда заданные прямые пересекаются или скрещиваются под углом
, тогда заданные прямые пересекаются или скрещиваются под углом 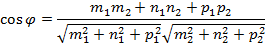
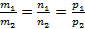 или прямые перпендикулярны, если
или прямые перпендикулярны, если 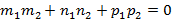 .
.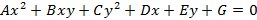
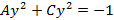 ;
;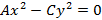 ;
;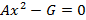 ;
;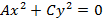 .
.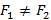 , которые называются фокусами. Множество всех точек
, которые называются фокусами. Множество всех точек 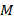 таких, что
таких, что 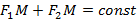 – сумма расстояний от
– сумма расстояний от 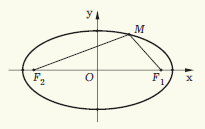
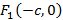 и
и 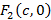 , таким образом межфокусное расстояние
, таким образом межфокусное расстояние 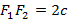 . Обозначим расстояние из определения
. Обозначим расстояние из определения 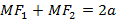 , в котором
, в котором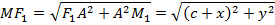
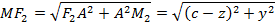
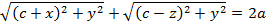
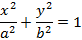
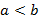 – эллипс втянут по вертикали, а его фокусы будут лежат на оси Oy. Если
– эллипс втянут по вертикали, а его фокусы будут лежат на оси Oy. Если 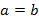 , тогда эллипс превратится в окружность, при этом межфокусное расстояние будет равно нулю и будут лежать в начале координат. Уравнение окружности в данном случае примет вид
, тогда эллипс превратится в окружность, при этом межфокусное расстояние будет равно нулю и будут лежать в начале координат. Уравнение окружности в данном случае примет вид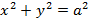
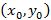 , тогда уравнение эллипса со смещенным центром примет вид
, тогда уравнение эллипса со смещенным центром примет вид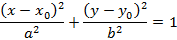
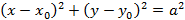
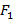 и
и 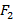 , которые называют фокусами, тогда множество точек M таких, что модуль разности от заданной точки до фокусов
, которые называют фокусами, тогда множество точек M таких, что модуль разности от заданной точки до фокусов 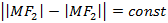 называется гиперболой.
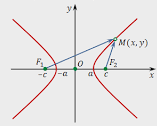
называется гиперболой.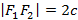 и расположим фокусы
и расположим фокусы 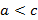 и рассмотрим точки
и рассмотрим точки 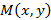 , такие что
, такие что 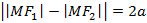 , тогда будут получены соотношения
, тогда будут получены соотношения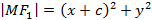
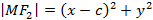
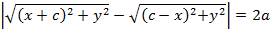
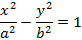
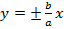 , к которым стремятся ветви гиперболы. Построение гиперболы относительно асимптотических прямых представлено на рисунке 18.
, к которым стремятся ветви гиперболы. Построение гиперболы относительно асимптотических прямых представлено на рисунке 18.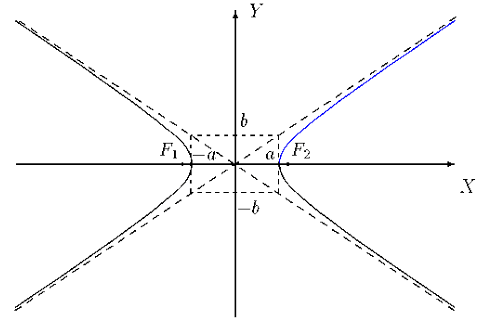
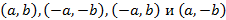 называется характеристическим. Его диагонали задают направление асимптотических прямых.
называется характеристическим. Его диагонали задают направление асимптотических прямых.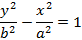
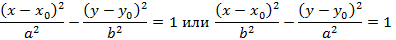
 – фокус и прямую
– фокус и прямую  – директриса, такая что
– директриса, такая что  . Множество всех точек M, равноудаленных от фокуса и директрисы
. Множество всех точек M, равноудаленных от фокуса и директрисы 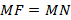 называется параболой. Обозначим p – расстояние от фокуса до директрисы и расположим
называется параболой. Обозначим p – расстояние от фокуса до директрисы и расположим 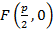 на си Ox, а директрису перпендикулярную Ox. Построение подставлено на рисунке 19.
на си Ox, а директрису перпендикулярную Ox. Построение подставлено на рисунке 19.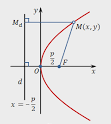
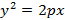
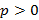 , тогда ветви параболы направлены в сторону увеличения x; при
, тогда ветви параболы направлены в сторону увеличения x; при 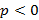 , тогда ветви параболы направлены в сторону уменьшения x. Если в рассматриваемом уравнении поменять роли x и y таким образом, что
, тогда ветви параболы направлены в сторону уменьшения x. Если в рассматриваемом уравнении поменять роли x и y таким образом, что 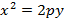 , тогда ветви параболы будут смотреть в сторону увеличения y (
, тогда ветви параболы будут смотреть в сторону увеличения y (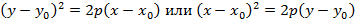
 . Если это уравнение рассмотреть в пространстве, то оно задаст поверхность параллельную Oz, которая называется цилиндром с образующей k.
. Если это уравнение рассмотреть в пространстве, то оно задаст поверхность параллельную Oz, которая называется цилиндром с образующей k.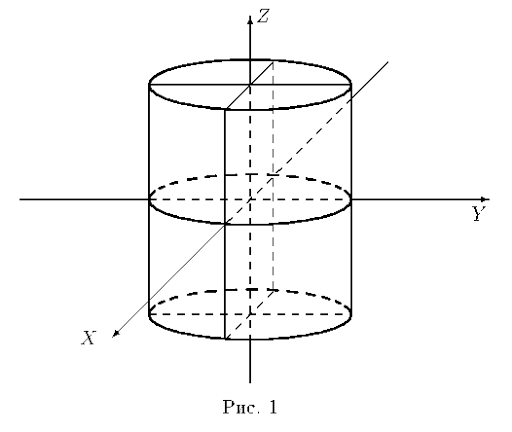
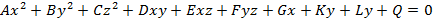
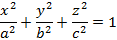
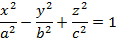
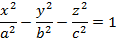
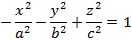
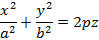
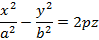
 . Например, множество действительных решений для уравнения
. Например, множество действительных решений для уравнения 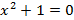 является пустым, хотя имеются два комплексных корня.
является пустым, хотя имеются два комплексных корня.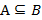
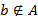 , тогда
, тогда 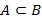 – A совпадает с B кроме некоторых элементов.
– A совпадает с B кроме некоторых элементов.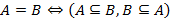 – A и B состоит из одинаковых элементов. Порядок следования элементов в обычном множестве не важен. В случае повторения элементов, учитывается каждый из них единожды с учетом его кратности.
– A и B состоит из одинаковых элементов. Порядок следования элементов в обычном множестве не важен. В случае повторения элементов, учитывается каждый из них единожды с учетом его кратности.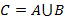 , состоящее из всех элементов этих множеств.
, состоящее из всех элементов этих множеств.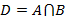 , состоящее из общих элементов для этих множеств.
, состоящее из общих элементов для этих множеств.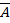 , состоящее из элементов универсального множества
, состоящее из элементов универсального множества 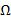 , которые не принадлежат множеству A.
, которые не принадлежат множеству A.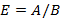 , состоящее из элементов множества A, которые не принадлежат B.
, состоящее из элементов множества A, которые не принадлежат B.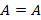 – любое равенство можно прочесть и справа на лево, и слева на право;
– любое равенство можно прочесть и справа на лево, и слева на право;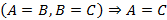 ;
;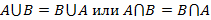 ;
;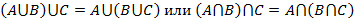 ;
;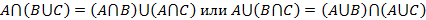 ;
;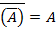 ;
;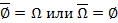 ;
;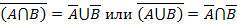 ;
;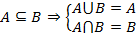 .
.


