
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства математического ожидания
1. Математическое ожидание постоянной величины равно самой постоянной: 2. Постоянный множитель можно выносить за знак математического ожидания: 3. Математическое ожидание алгебраической суммы конечного числа случайных величин равно алгебраической сумме их математических ожиданий:
4. Математическое ожидание произведения конечного числа независимых случайных величин равно произведению их математических ожиданий:
5. Математическое ожидание отклонения случайной величины от ее математического ожидания равно нулю: Дисперсия случайной величины На практике часто требуется оценить рассеяние возможных значений случайной величины вокруг ее среднего значения. Дисперсией
Дисперсия — это мера рассеяния случайной величины около ее математического ожидания. Если Х — дискретная случайная величина, то дисперсию вычисляют по следующим формулам: Свойства дисперсии случайной величины 1. Дисперсия постоянной величины С равна нулю: 2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат: 3. Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин: 4. Дисперсия разности двух независимых случайных величин равна сумме их дисперсий: Средним квадратическим отклонением Биномиальный закон распределения Если вероятность появления события А в каждом испытании постоянна и равна р, то число появлений события А — дискретная случайная величина Х, принимающая значения 0, 1, 2, …, Математическое ожидание и дисперсия случайной величины Х, распределенной по биномиальному закону, вычисляется по формулам: Распределение Пуассона
Если число испытаний велико, а вероятность появления события р в каждом испытании очень мала, то вместо формулы Бернулли пользуются приближенной формулой Пуассона:
|
|||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 81; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.122.46 (0.005 с.) |
 .
.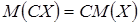 .
.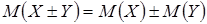 .
.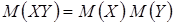 .
.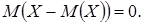
 случайной величины Х называется математическое ожидание квадрата ее отклонения от ее математического ожидания:
случайной величины Х называется математическое ожидание квадрата ее отклонения от ее математического ожидания: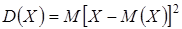 .
. , где а = М (Х);
, где а = М (Х); 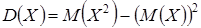 .
.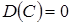 .
.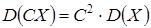 .
.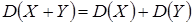 .
.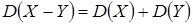 .
. случайной величины Х называется арифметическое значение корня квадратного из ее дисперсии:
случайной величины Х называется арифметическое значение корня квадратного из ее дисперсии: 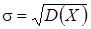 . Среднее квадратическое отклонение характеризует степень отклонения случайной величины от ее математического ожидания и имеет размерность значений случайной величины.
. Среднее квадратическое отклонение характеризует степень отклонения случайной величины от ее математического ожидания и имеет размерность значений случайной величины.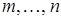 с вероятностями
с вероятностями 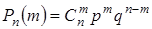 (формула Бернулли), где
(формула Бернулли), где 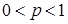 ,
, 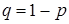 ,
, 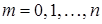 .
.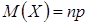 ,
,  .
.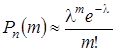 , где
, где 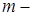 число появлений события в n независимых испытаниях; m принимает значения
число появлений события в n независимых испытаниях; m принимает значения 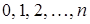 .
. 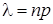 (среднее число появлений события в n испытаниях). Математическое ожидание и дисперсия случайной величины, распределенной по закону Пуассона, равны параметру, определяющему этот закон т. е.:
(среднее число появлений события в n испытаниях). Математическое ожидание и дисперсия случайной величины, распределенной по закону Пуассона, равны параметру, определяющему этот закон т. е.: 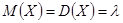 .
.


