
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вычисление длины дуги плоской кривой в декартовых
Координатах Если кривая задана уравнением
вычисляется по формуле:
Вычисление длины дуги кривой, заданной параметрически Если кривая задана параметрически
Пример. Найти длину дуги кривой а) Решение. а) Так как кривая задана в декартовой системе координат уравнением
б) Кривая задана параметрически, поэтому воспользуемся формулой (14). Найдём
Вычисление объёмов тел вращения Если тело образовано вращением вокруг оси OX криволинейной трапеции, ограниченной кривой
Пример. Найти объём тела, полученного вращением вокруг оси OX фигуры, ограниченной линиями: Решение. Построим криволинейную трапецию, вращением которой получается тело вращения (рис. 6). Чтобы получить искомый объем тела вращения, из объема
Несобственные интегралы Определение. Несобственными интегралами называются интегралы с бесконечными пределами (несобственные интегралы 1-го рода) и интегралы от неограниченных функций (несобственные интегралы 2-го рода). Пусть функция Определение. Если существует конечный предел Геометрический смысл несобственного интеграла
Аналогично определяются несобственные интегралы на промежутках
Рассмотрим, как вычисляются несобственные интегралы 1-го рода.
где Аналогично, Пример. Исследовать на сходимость интеграл Решение.
Рассмотрим несобственные интегралы 2-го рода. Пусть функция
При этом несобственный интеграл называется сходящимся, если существуют оба предела в правой части равенства, и расходящимся, если не существует хотя бы один из них. Геометрический смысл несобственного интеграла Пример. Исследовать на сходимость интеграл Решение. Интеграл рода, так как промежуток интегрирования содержит точку бесконечного разрыва
|
|||||||||||
|
Последнее изменение этой страницы: 2021-05-27; просмотров: 92; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.110.58 (0.011 с.) |
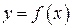 , функция
, функция 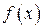 имеет непрерывную производную при всех
имеет непрерывную производную при всех 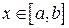 , то длина дуги
, то длина дуги 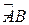 (рис. 4) этой кривой, заключённой между точками
(рис. 4) этой кривой, заключённой между точками 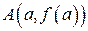 и
и 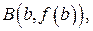

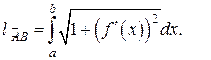 (13)
(13)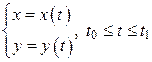 , и функции
, и функции  имеют непрерывные производные при всех
имеют непрерывные производные при всех 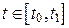 , то длина дуги
, то длина дуги  до
до  , вычисляется по формуле:
, вычисляется по формуле: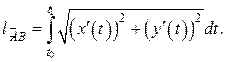 (14)
(14)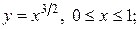 б)
б) 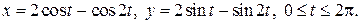
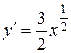 и подставим в (13):
и подставим в (13):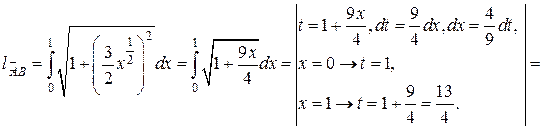
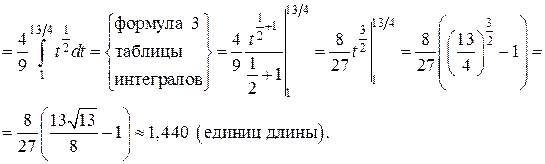
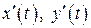 :
: 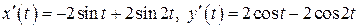 и подставим в (14):
и подставим в (14):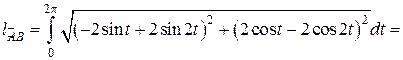
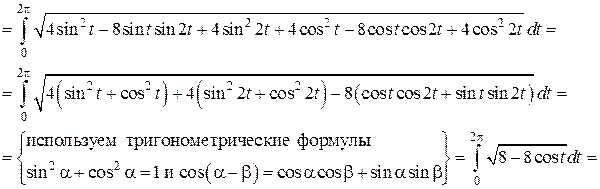
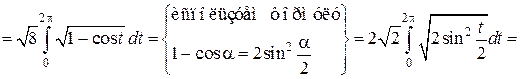
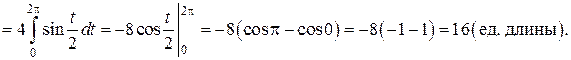
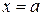 ,
, 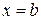 (рис. 5), то его объём вычисляется по формуле:
(рис. 5), то его объём вычисляется по формуле: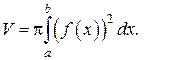 (15)
(15)

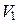 тела, полученного вращением фигуры ОАВС, вычтем объем
тела, полученного вращением фигуры ОАВС, вычтем объем 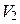 тела, полученного вращением фигуры ОАВ:
тела, полученного вращением фигуры ОАВ: 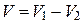 . По формуле (15) найдём
. По формуле (15) найдём  (ед. объёма);
(ед. объёма);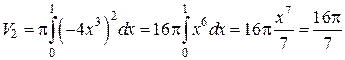 (ед. объёма);
(ед. объёма);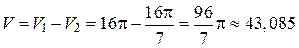 (ед. объёма).
(ед. объёма).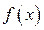 определена и непрерывна на полусегменте
определена и непрерывна на полусегменте 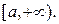 Возьмём любое
Возьмём любое 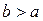 и рассмотрим интеграл
и рассмотрим интеграл 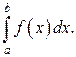
 то этот предел называется несобственным интегралом от функции
то этот предел называется несобственным интегралом от функции 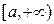 и обозначается
и обозначается 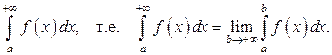 Говорят, что в этом случае несобственный интеграл существует или сходится. Если при
Говорят, что в этом случае несобственный интеграл существует или сходится. Если при 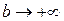 интеграл
интеграл 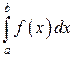 не имеет конечного предела, то говорят, что интеграл
не имеет конечного предела, то говорят, что интеграл 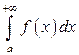 не существует или расходится.
не существует или расходится.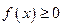 для всех
для всех 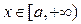 он выражает площадь неограниченной области, заключённой между линиями
он выражает площадь неограниченной области, заключённой между линиями  и осью ОХ.
и осью ОХ.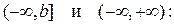
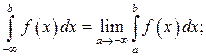
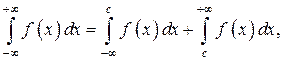 где с – любая точка на интервале
где с – любая точка на интервале 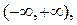 причём
причём 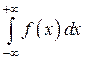 существует, если сходятся оба интеграла в правой части, и расходится, если расходится хотя бы один из них.
существует, если сходятся оба интеграла в правой части, и расходится, если расходится хотя бы один из них.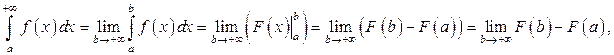
 первообразная для
первообразная для 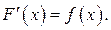
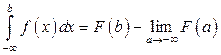 и
и 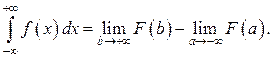
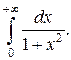
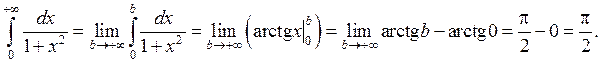 Значит, интеграл сходится и его величина равна
Значит, интеграл сходится и его величина равна 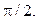
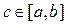 и непрерывна при
и непрерывна при 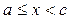 и
и  тогда полагают, что несобственный интеграл определяется формулой:
тогда полагают, что несобственный интеграл определяется формулой: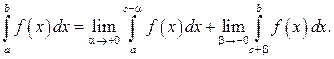 (16)
(16)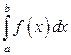 состоит в том, что при
состоит в том, что при 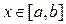 он выражает площадь неограниченной области, заключённой между линиями
он выражает площадь неограниченной области, заключённой между линиями 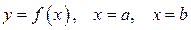 и осью ОХ.
и осью ОХ.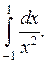
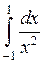 является несобственным интегралом 2-го
является несобственным интегралом 2-го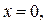 поэтому согласно формуле (16):
поэтому согласно формуле (16):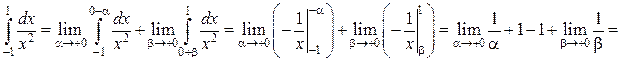
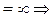 несобственный интеграл расходится.
несобственный интеграл расходится.


