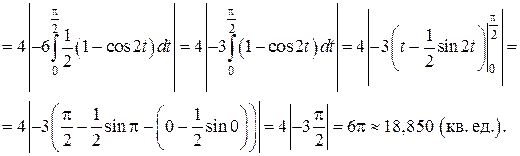Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Замена переменной в определённом интеграле
Теорема (о замене переменной в определённом интеграле). Пусть функция y = f (x) непрерывна на [ a, b ]. Если функция
Алгоритм замены переменной в определённом интеграле: 1. Старую и новую переменные связать соотношением 2. Найти связь между дифференциалами переменных x и t: 3. Определить новые пределы интегрирования α и β из уравнений 4. В искомом интеграле перейти к новой переменной по формуле (9) и заменить пределы интегрирования. Проинтегрировать и вычислить по формуле Ньютона–Лейбница (8). Пример. Вычислить определённый интеграл Решение.
Интегрирование по частям в определённом интеграле Формула интегрирования по частям (3) в случае определённого интеграла приобретает вид:
Пример. Вычислить определённый интеграл Решение.
Приложения определённого интеграла Определённый интеграл используется в различных приложениях: при вычислении площадей плоских фигур, длин дуг плоских кривых, объемов тел вращения, площадей поверхностей вращения, работы переменной силы на отрезке, пути, пройденного за промежуток времени, статических моментов и моментов инерции плоских дуг и фигур и т. д. Площади плоских фигур Вычисление площадей плоских фигур в декартовой системе координат Теорема. Если плоская фигура (рис. 1) ограничена линиями
Пример. Найти площадь фигуры, ограниченной линиями:
Решение. Построим схематический рисунок (рис. 2). Для построения параболы найдём координаты её вершины Площадь S фигуры, ограниченной обеими линиями (она отмечена на рис. 2 штриховкой) вычислим согласно формуле (11). Для определения нижнего и верхнего пределов интегрирования в этой формуле составим и решим уравнение Площадь полученной фигуры найдем по формуле (11), при
Вычисление площадей фигур, ограниченных линиями, заданными
Параметрически Площадь криволинейной трапеции, ограниченной сверху кривой, заданной параметрически уравнениями
Пример. Найти площадь фигуры, ограниченной линиями, заданными параметрически: Решение. Для построения фигуры составим таблицу значений координат (x, y) точек кривой, соответствующих различным значениям параметра
Нанесём точки (x, y) на координатную плоскость XOY и соединим их плавной линией. Когда параметр
Заметим, что для вычисления площади по формуле (9), построение чертежа не является обязательным, а носит иллюстративный характер. Длина дуги плоской кривой
|
|||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-27; просмотров: 115; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.157.39 (0.007 с.) |
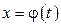 имеет непрерывную производную на отрезке
имеет непрерывную производную на отрезке  при
при 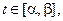 значение функции
значение функции 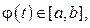 и, кроме того,
и, кроме того, 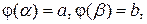 то справедлива формула
то справедлива формула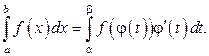 (9)
(9)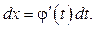
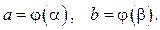
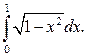
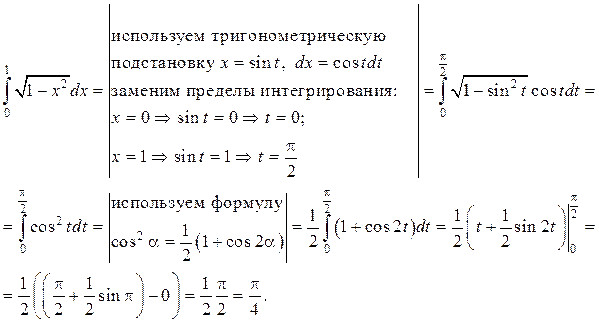
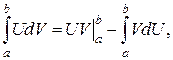 (10)
(10)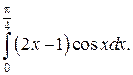
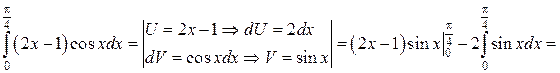
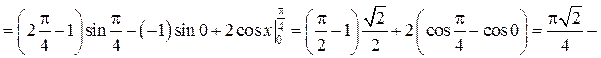
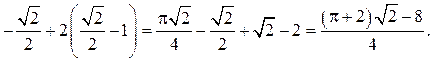

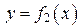 , где
, где 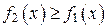 для всех
для всех 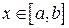 , и прямыми
, и прямыми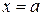 ,
, 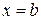 , то её площадь вычисляется по формуле:
, то её площадь вычисляется по формуле: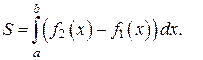 (11)
(11)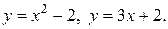
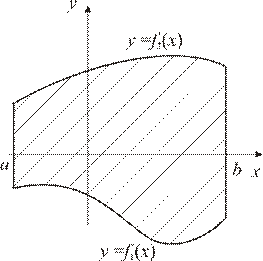

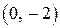 и направим верви параболы вверх. Для построения прямой достаточно двух точек, например
и направим верви параболы вверх. Для построения прямой достаточно двух точек, например 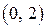 и
и  .
.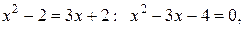
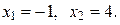 Итак, имеем
Итак, имеем 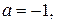
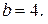
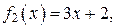
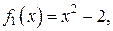 (поскольку
(поскольку 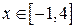 ), получаем:
), получаем: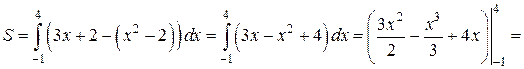
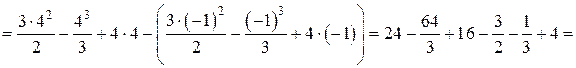
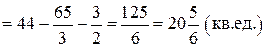
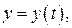
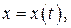 где функции
где функции 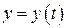 и
и 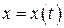 имеют непрерывные производные для всех
имеют непрерывные производные для всех 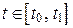 , и функция y (t) сохраняет знак на промежутке
, и функция y (t) сохраняет знак на промежутке 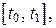 прямыми x = a, x = b, где a = x (t 0), b = x (t 1), и осью OX, вычисляется по формуле:
прямыми x = a, x = b, где a = x (t 0), b = x (t 1), и осью OX, вычисляется по формуле: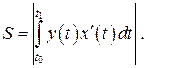 (12)
(12)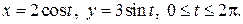
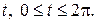
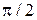
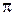
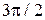

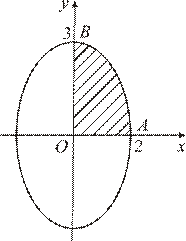
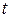 изменяется от
изменяется от 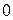 до
до 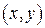 описывает эллипс (известно, что
описывает эллипс (известно, что 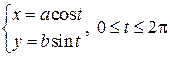 – параметрические формулы, задающие эллипс с полуосями a и b). Учитывая симметрию фигуры относительно координатных осей OX и OY, найдём её площадь S, умножив на 4 площадь криволинейной трапеции AOB. Согласно формуле (12) получим:
– параметрические формулы, задающие эллипс с полуосями a и b). Учитывая симметрию фигуры относительно координатных осей OX и OY, найдём её площадь S, умножив на 4 площадь криволинейной трапеции AOB. Согласно формуле (12) получим: