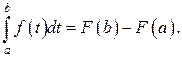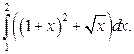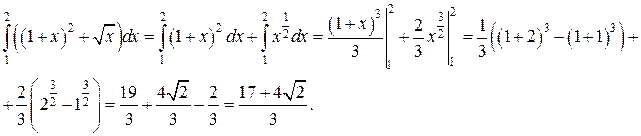Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определённый интеграл, теорема его существования
Рассмотрим функцию 1. Отрезок [ a,b ] разобьём точками 2. Внутри каждого отрезка
называемую интегральной суммой для функции 3. Обозначим
Определение. Если существует конечный предел при
При этом а называется нижним пределом, а b Если функция Определение. Криволинейной трапецией называется плоская фигура, ограниченная сверху графиком функции Можно показать, что площадь криволинейной трапеции с основанием [ a,b ] и ограниченной сверху графиком функции
Теорема (существования определённого интеграла). Если функция Свойства определённого интеграла
Замечание. Свойство 3 справедливо при любом расположении точки с по отношению к а и b при условии интегрируемости функции f (x) на большем из отрезков.
6) Если 7) Если 8) Теорема (о среднем значении функции на отрезке). Если функция
Определение. Средним значением функции
Формула Ньютона–Лейбница Теорема (о производной от интеграла с переменным верхним пределом). Пусть функция
Доказательство. Обозначим Следствие. Теорема (формула Ньютона–Лейбница). Если функция
где Доказательство. По следствию из предыдущей теоремы
Пример. Вычислить определённый интеграл Решение.
|
|||||
|
Последнее изменение этой страницы: 2021-05-27; просмотров: 69; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.166.61 (0.009 с.) |
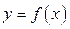 , которая непрерывна на отрезке [ a,b ]. Выполним следующие операции:
, которая непрерывна на отрезке [ a,b ]. Выполним следующие операции: на n произвольных частей и обозначим длины отрезков
на n произвольных частей и обозначим длины отрезков 
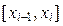 возьмём произвольную точку С i и вычислим в ней значение функции
возьмём произвольную точку С i и вычислим в ней значение функции 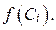 Составим сумму произведений значений функции
Составим сумму произведений значений функции  на
на 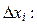
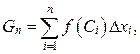 (5)
(5)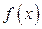 на отрезке [ a,b ].
на отрезке [ a,b ].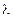 длину наибольшего из отрезков разбиений
длину наибольшего из отрезков разбиений 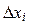 , т.е.,
, т.е., 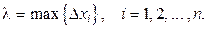 В равенстве (5) перейдём к пределу при
В равенстве (5) перейдём к пределу при 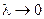 :
: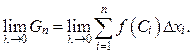 (6)
(6)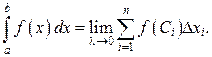 (7)
(7)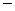 верхним пределом интегрирования.
верхним пределом интегрирования.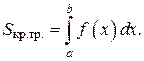
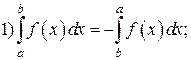

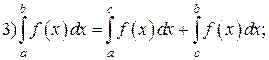

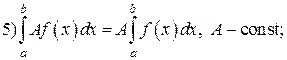
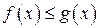 для всех
для всех 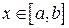 , то
, то 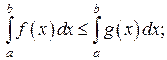
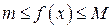 для всех
для всех 


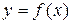 непрерывна на [ a,b ], тогда производная от определённого интеграла с переменным верхним пределом равна значению подынтегральной функции на этом верхнем пределе:
непрерывна на [ a,b ], тогда производная от определённого интеграла с переменным верхним пределом равна значению подынтегральной функции на этом верхнем пределе: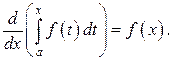
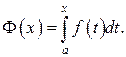 Придадим переменной х приращение
Придадим переменной х приращение 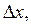 тогда
тогда 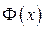 получит приращение
получит приращение 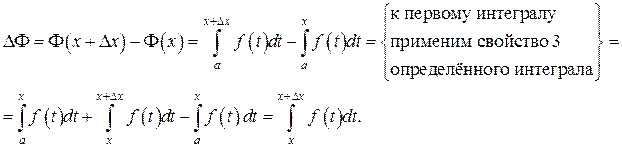
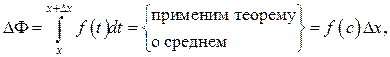 где с – некоторая точка между х и
где с – некоторая точка между х и 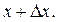 По определению производной имеем
По определению производной имеем 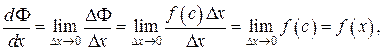 причём последнее равенство справедливо ввиду непрерывности функции
причём последнее равенство справедливо ввиду непрерывности функции 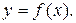
 первообразная для функции
первообразная для функции 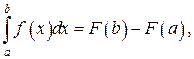 (8)
(8)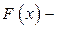 любая первообразная для функции
любая первообразная для функции 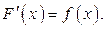
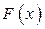 отличается от
отличается от 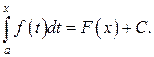 При
При 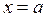 получим
получим 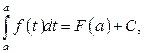 с другой стороны, по свойству 2 определённого интеграла
с другой стороны, по свойству 2 определённого интеграла 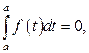 , следовательно,
, следовательно,  и
и  При
При 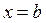 имеем
имеем