
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
З адание для контрольной работы. Вариант задания определяется остатком от деления номера зачетной книжки на число 40. ⇐ ПредыдущаяСтр 7 из 7
Вариант задания определяется остатком от деления номера зачетной книжки на число 40. А. Для образующей x (t) найти изображение x (z), для заданного периодследования импульсов Т. Б. Задана передаточная функция W РАЗ (s) разомкнутой САУ. Для неё: 1. Найти ДПФ разомкнутой W РАЗ (z) и замкнутой W ЗАМ (z) импульсной САУ. 2. Рассчитать переходный процесс способом разложения в ряд и табличным способом. Построить график и найти длительность переходного процесса в импульсах. 3. Рассчитать ДПФ последовательного корректирующего устройства, с которым в САУ переходный процесс примет заданный вид. 4. Составить разностное уравнение работы рассчитанного в п.3 корректирующего устройства.
Таблица 5.3 - Варианты задания к занятию №5
Продолжение таблицы 5.3
Продолжение таблицы 5.3
Продолжение таблицы 5.3
Продолжение таблицы 5.3
Продолжение таблицы 5.3
Продолжение таблицы 5.3
Вопросы для самоконтроля 1. Поясните способ описания импульсных сигналов z-изображениями и назовите достоинства и недостатки способа. 2. Поясните свойства неооднозначности оригиналов и z-изображений импульсных сигналов и как эту неоднозначность свести к минимуму? 3. Какова эквивалентная ДПФ последовательно соединенных звеньев? Как на расчет эквивалент-ной ДПФ влияет вид сигнала, которым связаны звенья последовательной цепи? 4. Какова эквивалентная ДПФ параллельно соединенных звеньев? 5. Какова эквивалентная ДПФ соединения звеньев с обратной связью? 6. Поясните вычисления дискретной передаточной функции, приведенные в примере. 7. Как рассчитать z-изображение переходного процесса? 8. Поясните метод расчета переходного процесса разложением в ряд.
9. Поясните табличный метод расчета переходного процесса. 10. Как рассчитать установившееся значение и продолжительность переходного процесса? Рекомендуемая литература: [2], [3], [4]. Расчеты оптимальных САУ вариационным методом и с использование принципа максимума Понтрягина
Рекомендации по изучению теоретических вопросов курса
Основные формулы и теоремы вариационного исчисления Вариационное исчисление позволяет отыскивать экстремали функционала, Основной теоремой вариационного исчисления является теорема Эйлера: если функция у=у (t) доставляет экстремум интегралу J, то она должна удовлетворять следующему дифференциальному уравнению (уравнению Эйлера): Решение уравнения Эйлера называется экстремалью. Применим уравнение Эйлера для определения формы линии на плоскости, которая кратчайшим способом соединяет две точки – А и В. Длина элементарного участка траектории согласно рис.5.1а равна
Длина всей линии
Здесь Находим частные производные от F и производную по аргументу х
Подставляем (5.3) в уравнение Эйлера (5.2)
откуда
Это уравнение прямой линии, соединяющей точки А и В. Постоянные интегрирования находятся из условия прохождения прямой чрез точки А и В. В общем случае уравнение Эйлера является дифференциальным уравнением второго порядка, и в решение его входят две произвольные постоянные. Эти произвольные постоянные должны быть определены из граничных условий. Простейшим случаем граничных условий является условие, чтобы кривая у (t) проходила через две заданные точки: В частных случаях уравнение Эйлера может превращаться в дифференциальное уравнение 1-го порядка, или даже в уравнение, не содержащее производных. Соответственно должно уменьшаться и число задаваемых граничных условий. Уравнение Эйлера является необходимым, но не достаточным условием, т.е. функции, удовлетворяющие уравнению (6.2), в некоторых случаях могут не доставлять экстремума. Для того чтобы решения уравнения Эйлера доставляли экстремум функционалу (6.1), достаточно, чтобы они не имели самосопряженных точек (условие Якоби) и выполнялось условие (Лежандра):
Задача о разыскании экстремума функционала (6.1) является простейшей задачей вариационного исчисления. фазовые переменные которого наложены ограничения типа неравенств. Главными достоинствами метода являются: - достаточно простое определение экстремалей, состоящих из кусочно-непрерывных функций, которые могут иметь разрывы (изменяться скачком); - учитываются ограничения типа неравенств (5.7). Теоремы принципа максимума справедливы для систем управления, поведение которых описывается системой дифференциальных уравнений первого порядка:
где уi - фазовые координаты объекта; uj - управления. Базовая постановка задачи оптимального формулируется следующим образом: отыскать управления и u (t), переводящие систему за время Т из положения у (0) в положение у (Т) и доставляющие экстремум функционалу Решение, полученное в такой постановке, затем распространяется (трансформируется) на оптимальные САУ произвольного типа. Переход к описанию объекта управления в виде системы уравнений вида (6.4) от линейного уравнения n -го порядка, например, осуществляется путем замены переменных
Тогда, обозначая
В число фазовых координат объекта включают еще величину у0, характеризующую текущее значение функционала, т.е.
Дифференциальное уравнение для координаты у0 записывается запишем окончательно систему уравнений задачи оптимального управления:
Важную роль в принципе максимума играют вспомогательные переменные ψ0 (t), ψ1 (t) ,…, ψn (t) и функция Н, называемая гамильтонианом Функции ψi (t) определяются из дифференциальных уравнений Если в (6.9) подставить функцию Н (6.8), то получим систему дифференциальных уравнений относительно функций ψi (t)
Теперь сформулируем основную теорему принципа максимума: Оптимальное управление и (t) с координатами u 1 (t) ,…, ur (t), доставляющее минимум функционалу J, одновременно обеспечивает максимум гамильтониану Н (6.8) при условии, что существует ненулевая непрерывная функция ψ (t) с координатами ψ1 (t) ,…, ψ r (t), удовлетворяющими уравнениям (6.9), т.е.
Особенностью принципа максимума является то, что вариационная задача нахождения функции и (t), доставляющей экстремум функционалу J, заменена гораздо более простой задачей математического анализа нахождения параметра и, доставляющего максимум вспомогательной функции Н (и).
Пример решения 1. Требуется найти экстремум функционала. Решим вариационным методом
при граничных условиях
Найдём частные производные:
Вычислим полную производную по t от Fy':
Составляем дифференциальное уравнение Эйлера вида:
или, после упрощений
Его общее решение имеет вид
Для нахождения произвольных постоянных C1 и C2 подставим решение в граничные условия:
Видно, что система имеет единственное решение. Решая эту систему, найдём значения C1 и C2:
и тогда уравнение экстремали имеет вид:
Уравнение Эйлера является необходимым, но не достаточным условием, т.е. функции в некоторых случаях могут не доставлять экстремума. Для того чтобы ре-шения уравнения Эйлера доставляли экстремум функционалу, достаточно, чтобы они не имели самосопряженных точек (условие Якоби) и выполнялось условие (Лежандра) для минимума
Условие выполняется 2. Решение с использованием принципов максимума Понтрягина
Переводим из операторной формы в дифференциальную
Составляем систему уравнений, заменяя индексами производные
Нахоим ДУ для координаты
Составляем систему уравнений оптимального управления
Вводим вспомогательные переменные, используя функцию гамильтониана
Находим частные производные
Получаем систему дифференциальных уравнений относительно переменной hi
Решим систему уравнений
Получаем неоднородное дифференциальное уравнение
Решение уравнения имеет вид
Сначала отыскиваем корни характеристического уравнения
Так как характеристическое уравнение имеет два корня, и корни не имеют комплексный вид, то решение ДУ имеет вид
Метод неопределенных коэффициентов
Получаем решение дифференциального уравнения
Оптимальное управление имеет вид
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-13; просмотров: 45; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.111.85 (0.087 с.) |
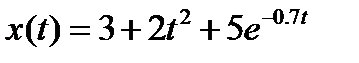

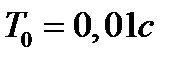




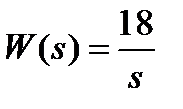




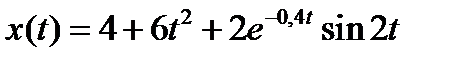
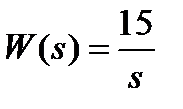

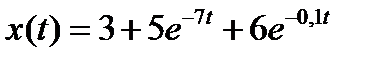

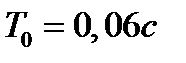
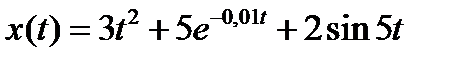


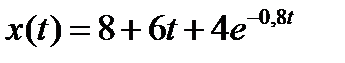

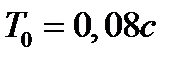
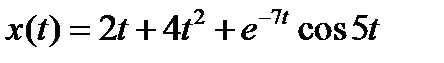


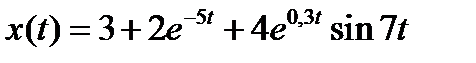



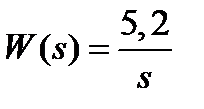
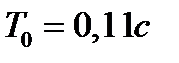

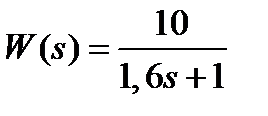

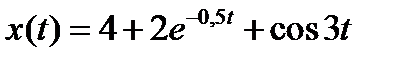


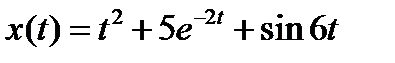


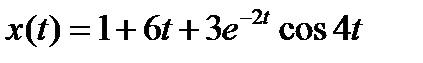

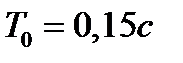







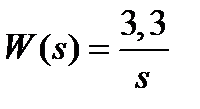


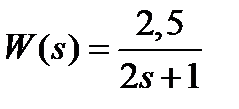
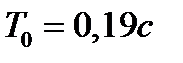



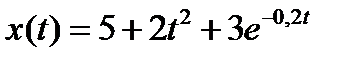
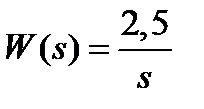


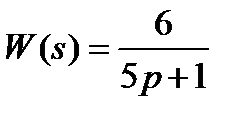
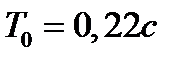
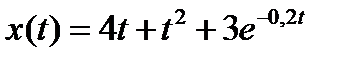


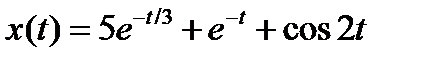
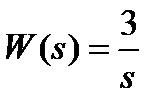


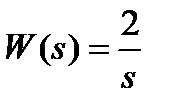
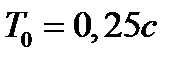

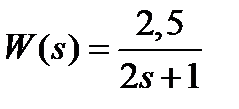






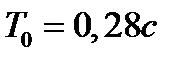


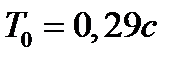

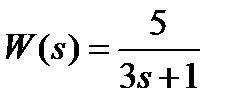
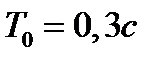
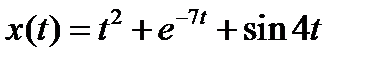

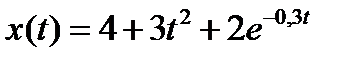


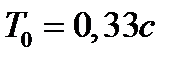



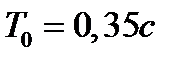
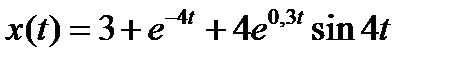
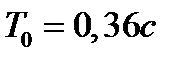

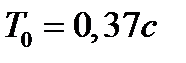

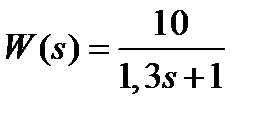



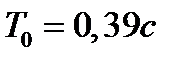
 (6.1)
(6.1)
 . (6.1)
. (6.1)
 (6.3)
(6.3)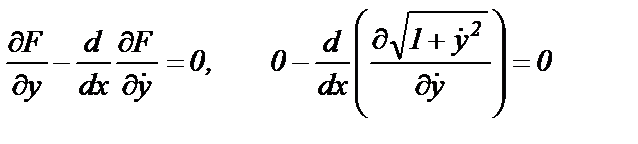 ,
,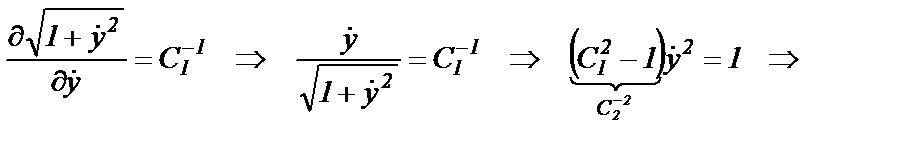

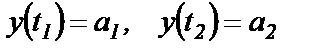 .
.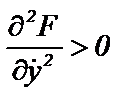 - для минимума и
- для минимума и  - для максимума функционала (6.1).
- для максимума функционала (6.1).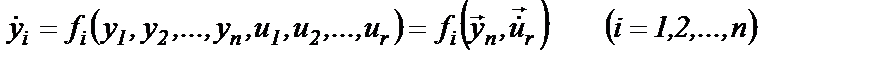 (6.4)
(6.4)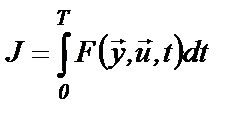 (6.5)
(6.5) и подстановки их в исходное уравнение. Пусть уравнение объекта с одним управляющим воздействием и имеет вид
и подстановки их в исходное уравнение. Пусть уравнение объекта с одним управляющим воздействием и имеет вид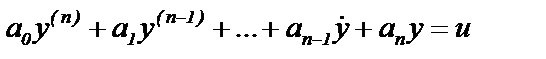
 можем записать систему п уравнений первого порядка, эквивалентную системе (6.4):
можем записать систему п уравнений первого порядка, эквивалентную системе (6.4):

 (6.6)
(6.6)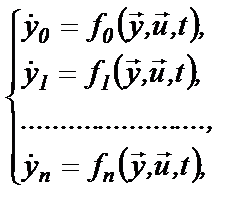 или в общем виде
или в общем виде 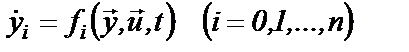 (6.7)
(6.7)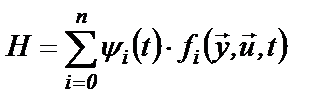 (6.8)
(6.8)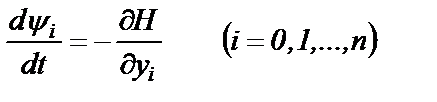 (6.9)
(6.9) (6.10)
(6.10)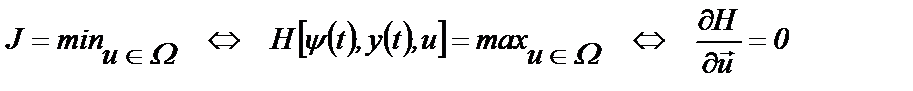
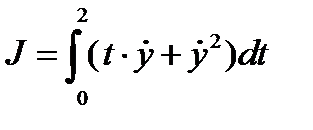
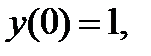
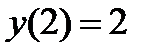 .
.
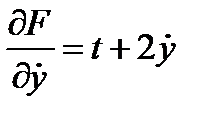 .
. .
.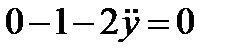 .
. .
. ,
,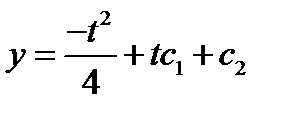 .
.

 .
.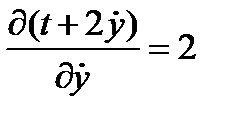 .
.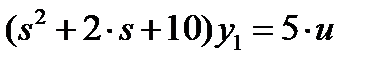 ,
,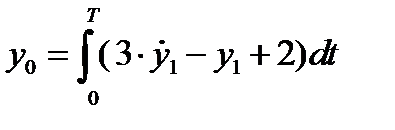 .
.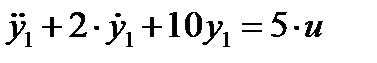 .
.

 , характеризующей текущее состояния функционала
, характеризующей текущее состояния функционала

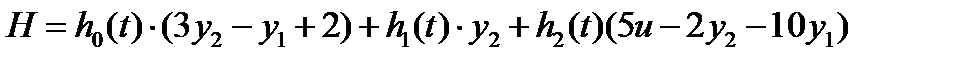
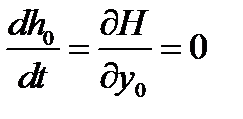 ,
,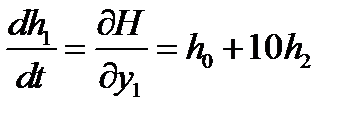 ,
, .
.
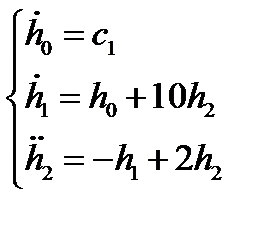
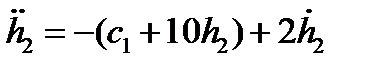 .
. .
. .
. ,
,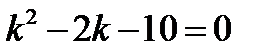 ,
,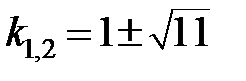 .
. ,
, .
. ,
,
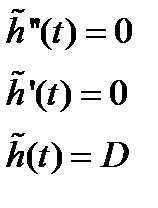
 ,
, .
.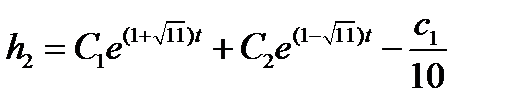 .
.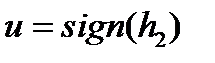 ,
, .
.


