Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
З адание для контрольной работы. Вариант задания определяется остатком от деления номера зачетной книжки на число 40.
Вариант задания определяется остатком от деления номера зачетной книжки на число 40. Для САУ (рисунок 3.1) объектом и регулятором с передаточными функциями, указанными в таблице 3.1, выполнить следующие действия: 1. Определить тип регулятора. 2. Произвести оценку устойчивости по критерию Гурвица. 3. Рассчитать ошибки регулирования для двух сигналов – x 1 и x 2.
Таблица 3.3 - Варианты задания к занятию №3
Продолжение таблицы 3.3
Продолжение таблицы 3.3
Вопросы для самоконтроля 1. Дайте определение устойчивости. Назовите прямые методы устойчивости и дайте характеристику области их применимости. 2. Перечислите основные прямые показатели, которыми оценивается качество работы САУ. 3. Что представляют собой критерии устойчивости? В чем состоят их преимущества перед прямыми методами? 4. Приведите формулировку критерия устойчивости. 5. Поясните процедуры определения допустимых настроек САУ по условию устойчивости. 6. Приведите вывод выражения установившейся ошибки регулирования. Рекомендуемая литература: [2], [3], [4]. Расчет переходного процесса в импульсной САУ и синтез регулятора по заданному переходному процессу
Рекомендации по изучению теоретических вопросов курса САУ является нелинейной, если в ней есть хотя бы один элемент, описываемый нелинейным либо алгебраическим, либо дифференциальных уравнений такого типа, линеаризация которого невозможна. Линеаризация может быть невозможна при наличии у характеристик точек излома, а также в тех случаях, когда сигналы звена нельзя считать малыми
Недостатки нелинейных САУ является сложность расчетов, обусловленная отсутствием аналитического описания (формул) нелинейностей. Для расчета нелинейных САУ разработаны эффективные специальные методы – метод фазовых переменных, гармонический метод. Метод фазовых траекторий является основным методом расчета нелинейных САУ. Основными достоинствами метода являются понижение порядка решаемых дифференциальных уравнений и наглядность решений. Пусть САУ описывается дифференциальным уравнением вида
Фазовые переменные у0, у1, у2,… этого дифференциального уравнения определяется как базовый сигнал у и производные от него:
В расчетах обычно используются две у 0, у 1 или три у 0, у 1, у 2 фазовые переменные. При двух фазовых переменных у0 и у1 порядок дифференциального уравнения понижается на единицу, а решение уравнения в фазовых переменных отображается в виде фазовой траектории на плоскости с координатами у 0 и у 1 по осям абсцисс и ординат. При трех фазовых переменных у 0 , у 1 и у 2 порядок дифференциального уравнения понижается на два, а решение уравнения в фазовых переменных отображается в виде фазовой траектории в трехмерном пространстве с координатными у 0 , у 1 и у 2. Понижение порядка дифференциального уравнения даже на единицу упрощает его решение и, как будет установлено ниже на примерах расчета, решения являются алгебраическими функциями, а не экспонентами и тригонометрическими функциями. Свойства фазовых траекторий. Фазовые траектории на плоскости у и
- ось абсцисс у пересекается фазовыми траекториями 3 и 4 под прямым углом, так как на этой оси
- линии отдельных траекторий 1 и 5 допускают разрывы по вертикали, если фазовое уравнение является алгебраическим, и разрывы не допускаются (линии 1 и 6), если фазовое уравнение дифференциальное любого порядка. Пусть дифференциальное уравнение линейной САУ 2-го порядка имеет вид
Очевидно, что для этой САУ принужденное решение упр будет нулевым. От вида корней характеристического уравнения будет зависеть не только вид свободного решения, но и устойчивость САУ, т.е. придет ли система к принужденному значению.
Расчет выполняется в следующей последовательности: 1. Описываем САУ системой обыкновенных уравнений: 2. Преобразуем дифференциальное уравнение системы в фазовое дифференциальное уравнение, которое будет содержать только фазовые переменные ε и 3. Подготавливаем фазовую плоскость к построению фазовых траекторий путем выделения на ней областей, в которых значение выходного сигнала и описывается формулой. 4. Задавшись начальными условиями ε0 и 5. Производим заключение о характере переходного процесса в САУ
Рассмотрим переходные процессы и фазовые траектории линейной САУ при различных корнях характеристического уравнения. 1. Корни чисто мнимые s 1,2=± jω. Переходным процессом являются незатухающие гармонические колебания, а фазовой траекторией является эллипс. Аналогичные замкнутые фазовые траектории имеются в нелинейных САУ с той разницей, что фазовая траектория не является эллипсом, а, поэтому, незатухающие переходные процессы являются негармоническими. Незатухающие негармонические колебания в нелинейных САУ называются автоколебаниями. 2. Корни комплексные s 1,2= α ± jβ. Переходным процессом являются затухающие гармонические колебания при α <0 и расходящиеся колебания при α >0. Фазовыми траекториями являются, соответственно, сходящиеся и расходящиеся спирали, навивающиеся вокруг особых точек – фокусов. 3. Корни действительные s 1= α 1 и s 2= α 2 одинакового знака. Переходным процессом являются затухающие экспоненциальные графики при α1,2<0 и расходящиеся экспоненциальные графики при α 1,2>0. Фазовыми траекториями являются, соответственно, сходящиеся и расходящиеся пучки, привязанные к особым точкам – узлам. 4. Корни действительные s 1= α 1 и s 2= α 2 разного знака. Переходным процессом являются расходящиеся экспоненциальные графики (рис.3.8а). Фазовыми траекториями являются серии расходящихся линий, которые по форме подобны седлу П ример решения
Задание Для нелинейной САУ, представленной на рисунке 4.2 рассчитать и построить переходный процесс на фазовой плоскости.
Рисунок 4.2 - Нелинейная САУ со звеном 2-го порядка с идеальным трехпозиционным реле
Решение 1. Описываем САУ системой обыкновенных уравнений: u = f (ε) - обобщенное описание нелинейности; (4.1) ε =0-у - уравнение элемента сравнения. Система из трех уравнений (4.1) содержит три сигнала-функции - сигнала-функции у, ε и и Нужно рассчитать выходной сигнал схемы – сигнал у, исключив из системы (4.1) сигналы ε и и. Однако, так как входным и выходным сигналами нелинейности являются, соответственно, ε и и, то желательно эти сигналы не исключать из системы уравнений, иначе потребуется перестройка графика нелинейности для иных входных и выходных сигналов, что сделать непросто. Учитывая третье уравнение ε =-у системы (4.1), исключим сигнал у. Получим следующее описание САУ
2. Преобразуем дифференциальное уравнение системы (4.2) в фазовое дифференциальное уравнение, которое будет содержать только фазовые переменные ε и
Система (3.13) обыкновенных уравнений после подстановки в нее (4.3) превратится в систему фазовых уравнений
Так как система фазовых уравнений содержит дифференциальное уравнение, то на фазовой траектории не должно быть разрывов и скачков по любой оси - ε и 3. Подготавливаем фазовую плоскость к построению фазовых траекторий путем выделения на ней областей, в которых значение выходного сигнала и описывается формулой. Так как выходной сигнал и нелинейности принимает всего три значения (-ит, 0 и ит ), то таких формул будет три – и=-ит, и=0 и и=ит. Поэтому, областей на фазовой плоскости будет также три.
Рисунок 4.3 - Фазовые траектории нелинейной САУ звеном 2-го порядка с идеальным трехпозиционным реле
Из графика нелинейности, приведенной на рис.4.2, видно, что при ε<-ε m значение выходного сигнала нелинейности равно –ит, при ε>ε m значение выходного сигнала нелинейности равно ит, а при -εт ≤ ε ≤ εт равно 0. Разбиение фазовой плоскости в соответствии с этими условиями на три области приведено на рис.3.10. Области отделены друг от друга линиями переключения ЛП1 и ЛП2, так как на этих линиях изменяются скачком (переключаются) значения сигнала и. 4. Задавшись начальными условиями ε0 и а). Область с и=ит. Дифференциальное фазовое уравнение согласно (4.4)
и его решение
Это парабола 0-1, симметричная относительно оси ε, с ветвями, направленными справа налево. б). Область с и=0. Дифференциальное фазовое уравнение согласно (3.15)
и его решение
Это прямая линия 1-2, параллельная оси ε. в). Область с и=-ит. Дифференциальное фазовое уравнение согласно (4.4)
и его решение
Это парабола 2-3, симметричная относительно оси ε, с ветвями, направленными слева направо. г). Область с и=0. Это прямая линия 3-4 (4.5), параллельная оси ε. 5. Заключение о характере переходного процесса в САУ. На рис.4.3 обозначены косой чертой одинаковые по величине отрезки. Их равенство следует из свойства симметричности графиков парабол и параллельности к оси абсцисс линий (4.5). Значит, фазовая траектория будет замкнутой линией, а переходный процесс будет периодическим незатухающим. Замкнутая линия - не эллипс и, поэтому, в САУ установятся автоколебания.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-13; просмотров: 46; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.200.180 (0.07 с.) |
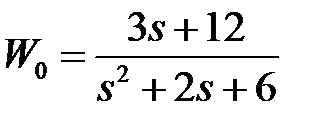
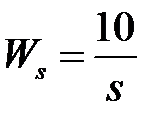
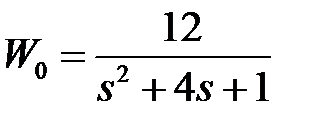
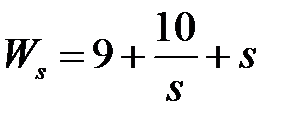


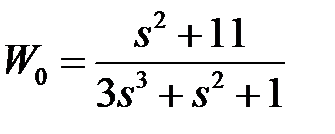
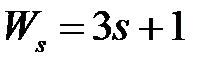

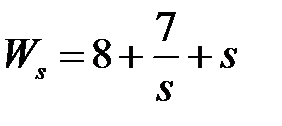

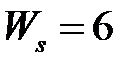
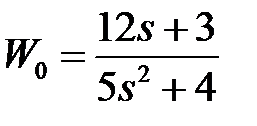


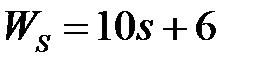
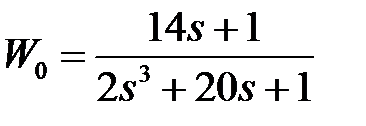


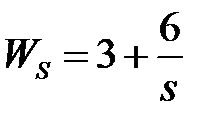


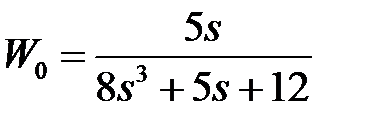
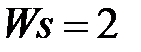
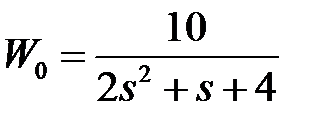

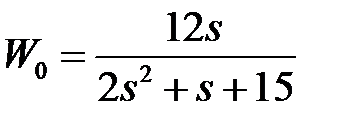
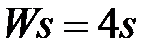
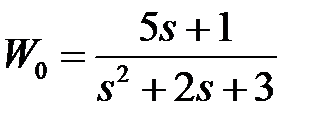
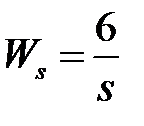
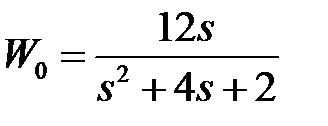
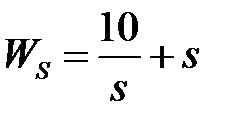
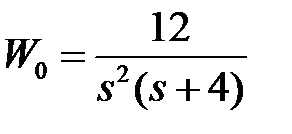


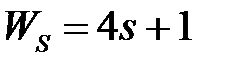
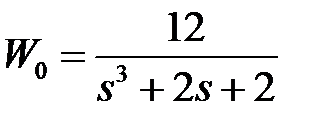


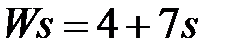
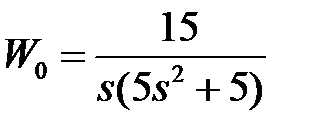



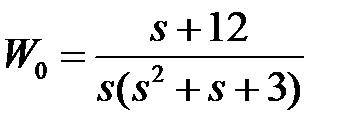
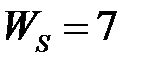




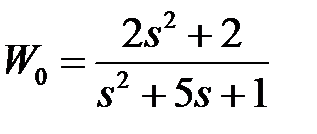
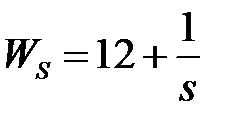



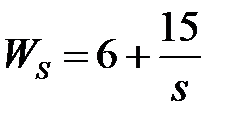
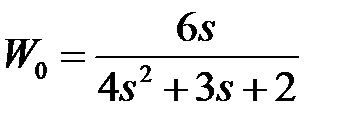
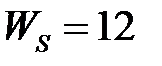
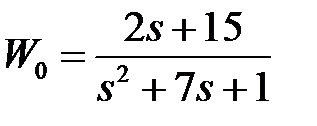
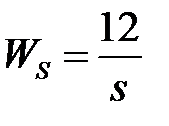
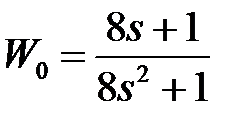



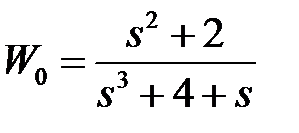
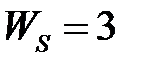

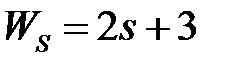
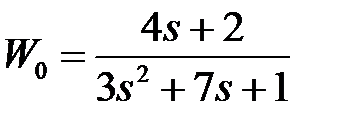
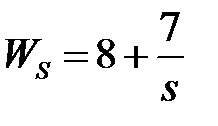
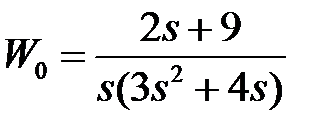
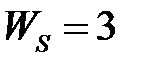
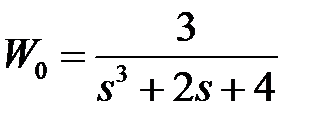


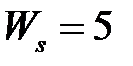


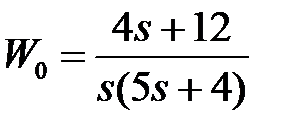
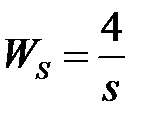

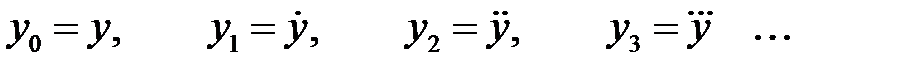
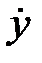 обладают следующими свойствами (рис.4.1):
обладают следующими свойствами (рис.4.1): - в верхней полуплоскости движение по фазовым траекториям 1 осуществляется слева направо (так как в верхней полуплоскости
- в верхней полуплоскости движение по фазовым траекториям 1 осуществляется слева направо (так как в верхней полуплоскости  и, поэтому значение у только возрастает), а в нижней – справа налево по траекториям 2;
и, поэтому значение у только возрастает), а в нижней – справа налево по траекториям 2;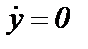 и, поэтому у не изменяется;
и, поэтому у не изменяется;
 и не будет содержать время t.
и не будет содержать время t. , решаем дифференциальное уравнение системы по областям, очерченными линиями переключения
, решаем дифференциальное уравнение системы по областям, очерченными линиями переключения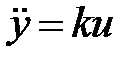 - дифференциальное уравнение линейного звена;
- дифференциальное уравнение линейного звена;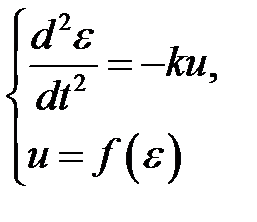 (4.2)
(4.2)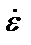 и не будет содержать время t. Выполним преобразования
и не будет содержать время t. Выполним преобразования и
и 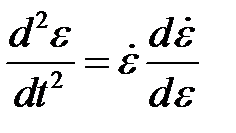 (4.3)
(4.3) (4.4)
(4.4) (см. рис.4.3).
(см. рис.4.3).
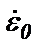 , решаем дифференциальное уравнение системы по областям, очерченными линиями переключения ЛП1 и ЛП2.
, решаем дифференциальное уравнение системы по областям, очерченными линиями переключения ЛП1 и ЛП2.


 (4.5)
(4.5)