
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Функциональная, статистическая зависимости системы случайных величин. Условная средняя ⇐ ПредыдущаяСтр 5 из 5
Во многих задачах требуется установить и оценить зависимость изучаемой случайной величины Y от одной или нескольких случайных величин. Две случайные величины X и Y могут быть связаны между собой функциональной, статистической зависимостью или быть независимыми. Функциональная зависимость (строгая, жесткая) встречается крайне редко, т.к. одна случайная величина или обе подвержены действию случайных факторов. Причем среди случайных факторов могут быть общие. В этом случае возникает статистическая зависимость.
Пример. СВ X зависит от случайных факторов Z1; Z2; Z3 СВ Y зависит от случайных факторов Z2; Z3; Z4; Z5 Т.к. среди этих факторов есть общие, то между случайными величинами X и Y есть статистическая зависимость.
Определение. Статистической зависимостью называется зависимость, при которой изменение одной из величин влечет за собой изменение распределения другой величины.
Если статистическая зависимость проявляется в том, что при изменении одной величины, изменяется среднее значение другой, то такая зависимость называется корреляционной. Корреляционная зависимость - это мягкая зависимость в отличии от жесткой функциональной.
В качестве оценок математических ожиданий принимают условные средние, которые найдены по данным наблюдений (по выборке). Определение. Условным средним
Например, при значении x =2 наблюдавшиеся значения Y: y1=3, y2=7, y3=4. Условное среднее Аналогично условным средним
Линейная корреляционная зависимость. Выборочные уравнения прямой регрессии Y на X. Коэффициент корреляции В результате n независимых опытов получено n пар чисел (xi; yi).
Ограничимся приближенным представлением (а точное представление здесь не возможно), что между Х и Y существует корреляционная зависимость, близкая к линейной. Параметры этого линейного уравнения a0 и a1 находят методом наименьших квадратов путем составления и решения системы нормальных уравнений.
Система для МНК (метода наименьших квадратов)
Метод наименьших квадратов «рассчитан» на то, чтобы квадраты отклонений значений (xi;yi) от прямой линии были наименьшими.
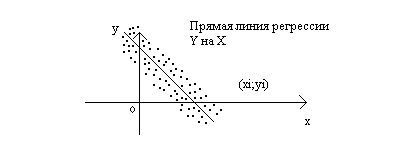
Графическое представление системы (x;y) на плоскости называется полем корреляции. Определение. Выборочным уравнением прямой регрессии Y на X называется уравнение
x - переменная величина; σ x, σ y - средние квадратические отклонения X и Y; rB - коэффициент корреляции. Коэффициент корреляции отражает связь между признаками X и Y. Если коэффициент корреляции близок к нулю (rB ≈0), то X и Y не зависимы и никакого влияния друг на друга не оказывают, т.е. не коррелированные. Если коэффициент корреляции близок к одному (rB ≈1), то между X и Y существует корреляционная зависимость близкая к линейной функциональной. Оценить значимость коэффициента корреляции можно по критерию Стьюдента.
Пример Проведены 20 независимых опытов по изучению зависимости случайных величин X и Y а) построить график зависимости (поле корреляции) между переменными X и Y, по которому найти модель уравнения регрессии; б) рассчитать параметры уравнения регрессии методом наименьших квадратов (МНК); в) оценить тесноту связи между переменными с помощью показателей корреляции и детерминации: г) оценить значимость коэффициентов корреляции и регрессии по критерию Стьюдента при уровне значимости
Решение. а) В прямоугольной системе координат строим график зависимости переменных X и Y На график наносим точки Визуально анализируя характер расположения точек на графике, приходим к выводу, что связь между переменными X и Y может быть выражена линейным уравнением регрессии
б) Параметры уравнения регрессии находим методом наименьших квадратов, путем составления и решения системы нормальных уравнений:
Составим расчетную таблицу.
Тогда система примет вид:
Решим систему по формулам Камера.
Следовательно, Таким образом, уравнение регрессии Y на X имеет вид:
Построим линию регрессии Y на X по таблице
Линия регрессии изображена на рисунке.
в) При линейной зависимости степень тесноты связи между X и Y определяется с помощью коэффициента корреляции
Найдем:
Вычислим средние квдратические отклонения
Отсюда, Т.к. Коэффициент детерминации равен г) Оценить значимость коэффициента корреляции. Нулевая гипотеза Конкурирующая гипотеза Для проверки нулевой гипотезы применим критерий Стьюдента. Уровень значимости По таблице критических точек распределения Стьюдента по уровню значимости
Т.к. Вывод: выборочный коэффициент корреляции значим, случайные величины X и Y коррелированы.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-12; просмотров: 341; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.17.20 (0.02 с.) |
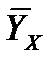 называется среднее арифметическое значение наблюдавшихся значений Y, соответствующих значению X = x.
называется среднее арифметическое значение наблюдавшихся значений Y, соответствующих значению X = x.
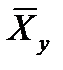 называется среднее арифметическое наблюдавшихся значений
называется среднее арифметическое наблюдавшихся значений  , соответствующих значению Y = y.
, соответствующих значению Y = y.
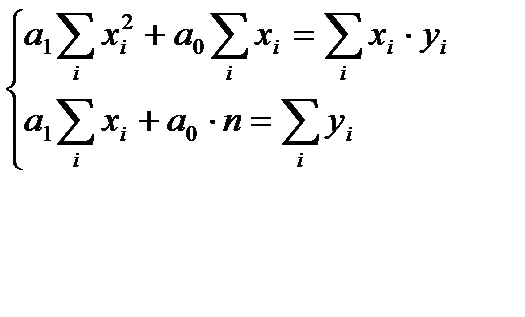
 - выборочное уравнение прямой регрессии Y на X;
- выборочное уравнение прямой регрессии Y на X;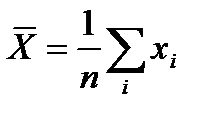 - среднее арифметическое значение X;
- среднее арифметическое значение X;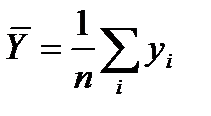 -среднее арифметическое значение Y;
-среднее арифметическое значение Y; ;
;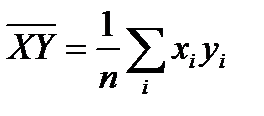 .
.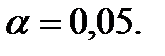
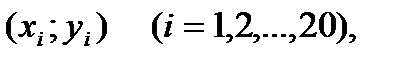 координаты которых соответствуют значениям переменных X и Y.
координаты которых соответствуют значениям переменных X и Y.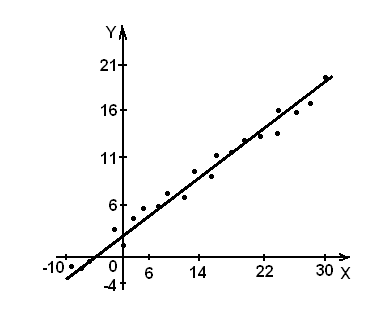
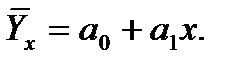
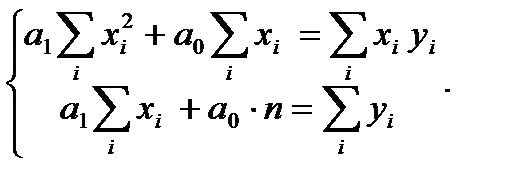

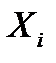

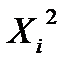

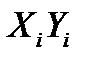
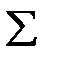
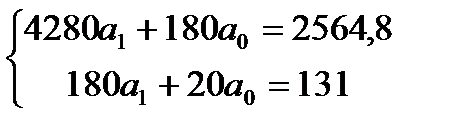
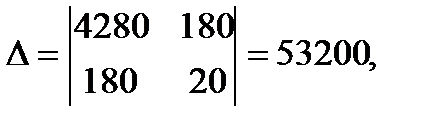
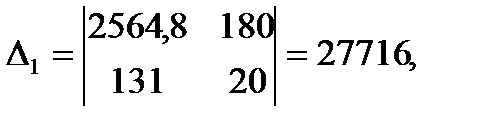
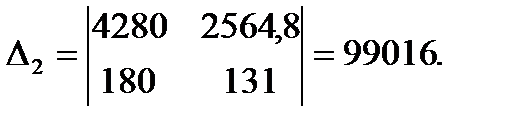
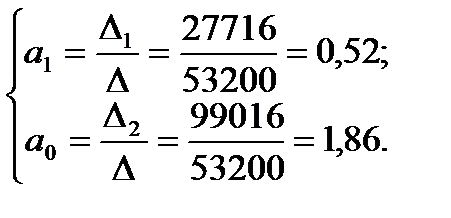
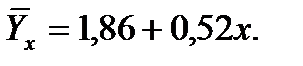

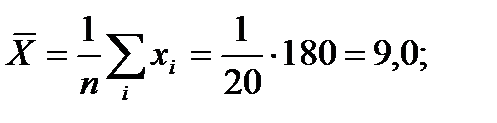
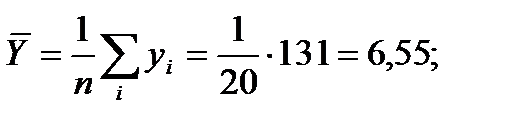
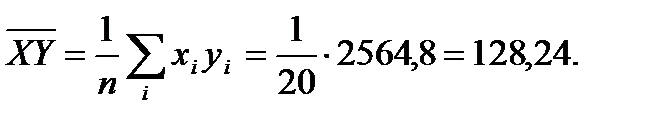
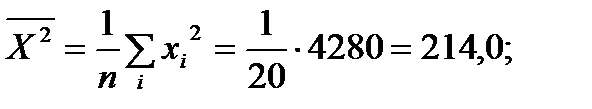
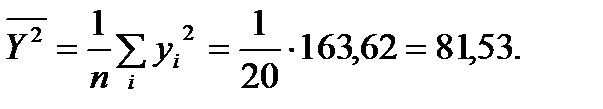
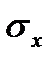 и
и 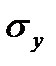 :
: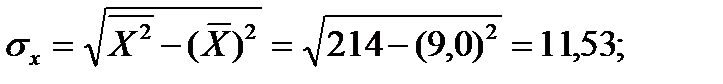


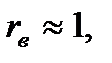 то между признаками связь очень тесная, близкая к линейной функциональной.
то между признаками связь очень тесная, близкая к линейной функциональной.
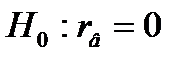 - переменная X не оказывает существенного влияния на Y.
- переменная X не оказывает существенного влияния на Y.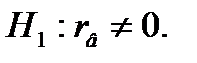
 Найдем наблюдаемое значение критерия
Найдем наблюдаемое значение критерия 
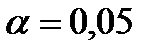 и числу степеней свободы
и числу степеней свободы 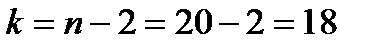 найдем критическую точку
найдем критическую точку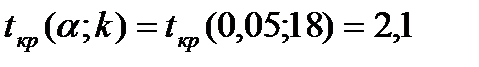 двусторонней критической области.
двусторонней критической области.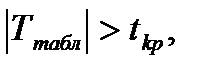 то нулевую гипотезу отвергаем.
то нулевую гипотезу отвергаем.


