
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Раздел № 2 «Математическая статистика»Стр 1 из 5Следующая ⇒
КУРС ЛЕКЦИЙ «Теория вероятностей. Математическая статистика» Семестр для студентов очной формы обучения Раздел № 2 «Математическая статистика» Волгодонск Предмет и задачи математической статистики Математическая статистика занимается изучением массовых явлений методами теории вероятностей. К задачам математической статистики относятся: 1. Разработка методов сбора информации, способы группировки статистических сведений полученных в результате наблюдений или специально поставленных экспериментов. 2. Разработка методов анализа полной информации в зависимости от целей исследования. Сюда относятся: а) оценка неизвестной вероятности события, оценка неизвестной функции распределения, оценка параметров распределения, оценка зависимости одной случайной величины от другой. б) проверка статистических гипотез о виде неизвестного распределения. Современная математическая статистика разрабатывает способы определения числа необходимых исследований до начала исследования, т.е. планирует эксперимент. Современную МС определяют как науку о принятии решений в условиях неопределенности. Генеральная и выборочная совокупности Пусть требуется изучить совокупность одинаковых объектов относительно некоторого качественного или количественного признака. Например: Для партии деталей качественный признак – их стандартность, а количественный – контролируемый размер деталей. Иногда проводят сплошное обследование каждого объекта. Если совокупность содержит большое число объектов, то провести сплошное обследование невозможно. В таких случаях случайным образом отбирают ограниченное число объектов и их изучают. Опр: Выборочной совокупностью (выборкой) называют совокупность случайно выбранных объектов. Опр: Генеральной совокупностью называется совокупность из которой произведена выборка. Опр: Объемом совокупности называется число объектов. Объем генеральной совокупности N Объем выборки n Например: Из партии в 1000 деталей выбрано 100. N =1000; n =100 Пример: В условиях предыдущей задачи, таблица (**), построить эмпирическую функцию распределения и ее график.
0, x ≤ 0,1 5/25 0,1< x ≤ 0,3
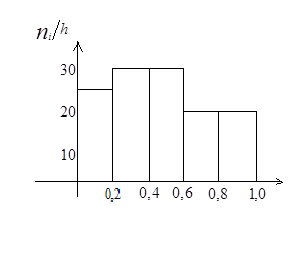
(5+6+6)25= 17/25 0,5< x ≤ 0,7 (5+6+6+4)/25= 21/25 0,7< x ≤ 0,9 (5+6+6+4+4)/25= 25/25= 1 x > 0,9 График Полигон и гистограмма Для наглядности строят различные графики статистического распределения, в частности полигон и гистограмму. Полигоном частот называется ломаная, звенья которой соединяют точки с координатами ( Построить полигон частот по распределению (таблица (**)). В случае непрерывного распределения для интервалов строят гистограмму частот. Находят шаг интервала h. На оси абсцисс откладывают частичный интервал, на оси ординат плотность частоты Гистограммой частот называется ступенчатая фигура, состоящая из прямоугольников. Основания прямоугольников – частичные интервалы, а высота – плотность частоты. Интервальные оценки Опр: Интервальной называют оценку, которая определяется 2-мя числами, концами интервала. Опр: Доверительным называется интервал, который с заданной надежностью покрывает оцениваемый параметр. Надежность оценки - это вероятность попадания в доверительный интервал. Рассмотрим 3 интервальные оценки параметров нормально распределенного признака 1. Интервальной оценкой с надежностью
Где точность Параметр t находят из соотношения Пример: Найти доверительный интервал для оценки с надежностью
Интервальная оценка Находим t, По таблице найдем t=1,96
2. Интервальной оценкой с надежностью Пример: По данным 9 независимых равноточных измерений некоторой физической величины из генеральной совокупности найдено выборочное среднее квадратическое отклонение равно Оценить истинное значение физической величины с надежностью По таблице
3. Интервальной оценкой с надёжностью σ нормально распределённого количественного признака Х по исправленному выборочному среднему квадратическому отклонению S служит интервал
где q находят по таблицам по известным n и Пример. По данным выборки объёма n =16 найдено исправленное выборочное среднее квадратическое отклонение S =1 нормально распределённого признака в генеральной совокупности. Найти с надёжностью 1(1-0,44) < σ <1(1+0,44) 0,56 < σ <1,44. Определение. Статистической называют гипотезу о виде неизвестного распределения и о параметрах известного распределения.
«Гипотеза – “есть ли жизнь на Марсе?”, статистической не является».
Определение. Нулевой (основной) называют выдвинутую гипотезу H 0. Конкурирующей (альтернативной) называют гипотезу H 1, которая противоречит основной.
Если нулевая гипотеза отвергается, то ее место занимают конкурирующая гипотеза. Например: Для нормальной случайной величины нулевая гипотеза H 0: a =10, а конкурирующая гипотеза H 1: a ≠10. Эти гипотезы о равенстве некоторого параметра известного распределения.
Определение. Различают гипотезы с одним или несколькими числом предположений. Гипотеза с одним числом предположений называется простой, гипотеза с большим количеством предположений называется сложной. Простая H 0: а=10 (σ -известно и равно 1) Сложная H 0: а=10 (σ -неизвестно)
При принятии гипотезы можно либо принимать нулевую гипотезу, либо ее отвергнуть, потому что выдвинутая гипотеза может быть правильной, а может быть не правильной. Если отвергается правильная гипотеза, то совершается ошибка первого рода. Если принимается конкурирующая гипотеза, то совершается ошибка второго рода. Последствия этих ошибок разные.
Определение. Статистическим критерием называют случайную величину K, которая служит для проверки нулевой гипотезы. Для проверки гипотезы по данным выборки вычисляют частные значения, входящие в критерий величин и получают наблюдаемое значение критерия.
Определение. Наблюдаемым значением критерия K набл называют значение, полученное по выборке.
Определение. Критической областью называют совокупные значения критерия, при которых нулевую гипотезу отвергают, а областью принятия гипотезы – там, где нулевую гипотезу принимают.
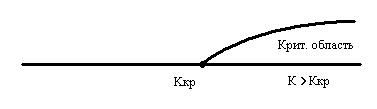
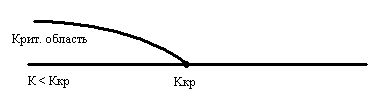
Основной принцип проверки статистических гипотез состоит в следующем: если наблюдаемое значение критерия принадлежит критической области, то нулевую гипотезу нужно отвергнуть. Определение. Критической точкой K крит называют точку, разделяющую критическую область и область принятия гипотезы. Различают правосторонние, левосторонние и двусторонние критические области. Правосторонняя Левосторонняя
Двусторонняя
K > KKP Для нахождения критической точки ККР задаются малой величиной: уровнем значимости α. Уровень значимости α – это вероятность попадания в критическую область. Для правосторонней области: Для левосторонней области: Для двусторонней области: Для уровня значимости предполагается, что нулевая гипотеза справедлива. Определение. Мощностью критерия называется вероятность попадания его в критическую область при условии, что конкурирующая гипотеза справедлива. Важно чтобы мощность критерия была максимальной.
Замечание. По критерию согласия Пирсона объем выборки должен быть велик (n≥50).
Пример. По данным выборки получены эмпирические и теоретические частоты. Проверить гипотезу о нормальном распределении генеральной совокупности по критерию согласия Пирсона при заданном уровне значимости. Эмпирические и теоретические частоты заданы таблицей.
Уровень значимости α=0,05
Вычислим наблюдаемое значение критерия Составим расчетную таблицу.
Контроль
Найдем число степеней свободы K =8-3=5 По уровню значимости α=0,05 и числу степеней свободы K =5 по таблице критических точек χ2кр(α;κ) находим критическую точку правосторонней критической области χ2кр(0,05;5)=11,1.
Т.к. χ2набл< χ2кр, то нет основания отвергнуть гипотезу о нормальном распределении генеральной совокупности, т.е. эмпирические и теоретические частоты различаются не значимо (их различие носит случайный характер).
Элементы теории корреляции Пример. СВ X зависит от случайных факторов Z1; Z2; Z3 СВ Y зависит от случайных факторов Z2; Z3; Z4; Z5 Т.к. среди этих факторов есть общие, то между случайными величинами X и Y есть статистическая зависимость.
Определение. Статистической зависимостью называется зависимость, при которой изменение одной из величин влечет за собой изменение распределения другой величины.
Если статистическая зависимость проявляется в том, что при изменении одной величины, изменяется среднее значение другой, то такая зависимость называется корреляционной. Корреляционная зависимость - это мягкая зависимость в отличии от жесткой функциональной.
В качестве оценок математических ожиданий принимают условные средние, которые найдены по данным наблюдений (по выборке). Определение. Условным средним
Например, при значении x =2 наблюдавшиеся значения Y: y1=3, y2=7, y3=4. Условное среднее Аналогично условным средним
Определение. Выборочным уравнением прямой регрессии Y на X называется уравнение
x - переменная величина; σ x, σ y - средние квадратические отклонения X и Y; rB - коэффициент корреляции. Коэффициент корреляции отражает связь между признаками X и Y. Если коэффициент корреляции близок к нулю (rB ≈0), то X и Y не зависимы и никакого влияния друг на друга не оказывают, т.е. не коррелированные. Если коэффициент корреляции близок к одному (rB ≈1), то между X и Y существует корреляционная зависимость близкая к линейной функциональной.
Оценить значимость коэффициента корреляции можно по критерию Стьюдента.
Пример Проведены 20 независимых опытов по изучению зависимости случайных величин X и Y а) построить график зависимости (поле корреляции) между переменными X и Y, по которому найти модель уравнения регрессии; б) рассчитать параметры уравнения регрессии методом наименьших квадратов (МНК); в) оценить тесноту связи между переменными с помощью показателей корреляции и детерминации: г) оценить значимость коэффициентов корреляции и регрессии по критерию Стьюдента при уровне значимости
Решение. а) В прямоугольной системе координат строим график зависимости переменных X и Y На график наносим точки Визуально анализируя характер расположения точек на графике, приходим к выводу, что связь между переменными X и Y может быть выражена линейным уравнением регрессии б) Параметры уравнения регрессии находим методом наименьших квадратов, путем составления и решения системы нормальных уравнений:
Составим расчетную таблицу.
Тогда система примет вид:
Решим систему по формулам Камера.
Следовательно, Таким образом, уравнение регрессии Y на X имеет вид:
Построим линию регрессии Y на X по таблице
Линия регрессии изображена на рисунке.
в) При линейной зависимости степень тесноты связи между X и Y определяется с помощью коэффициента корреляции
Найдем:
Вычислим средние квдратические отклонения
Отсюда, Т.к. Коэффициент детерминации равен г) Оценить значимость коэффициента корреляции. Нулевая гипотеза Конкурирующая гипотеза Для проверки нулевой гипотезы применим критерий Стьюдента. Уровень значимости По таблице критических точек распределения Стьюдента по уровню значимости
Т.к. Вывод: выборочный коэффициент корреляции значим, случайные величины X и Y коррелированы. КУРС ЛЕКЦИЙ «Теория вероятностей. Математическая статистика» Семестр для студентов очной формы обучения Раздел № 2 «Математическая статистика» Волгодонск
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-12; просмотров: 53; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.136.165 (0.108 с.) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 (x) = (5+6)/25= 11/25 0,3< x ≤ 0,5
(x) = (5+6)/25= 11/25 0,3< x ≤ 0,5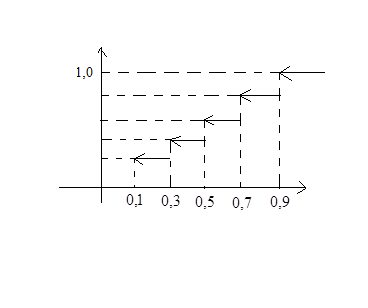
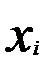 ;
; 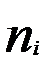 ). На оси абсцисс откладывают варианты
). На оси абсцисс откладывают варианты 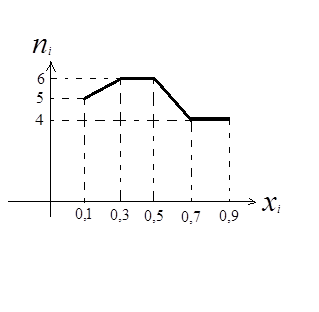
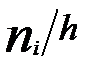 .
.
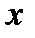 генеральной совокупности.
генеральной совокупности.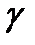 математического ожидания, а нормально распределенного количественного признака
математического ожидания, а нормально распределенного количественного признака 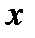 по выборочной средней
по выборочной средней 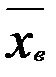 при измененном среднем квадратическом отклонении
при измененном среднем квадратическом отклонении  генеральной совокупности служит интервал
генеральной совокупности служит интервал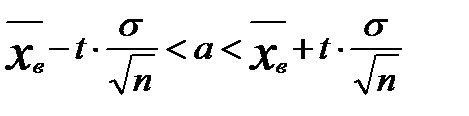
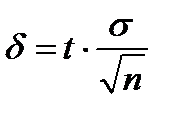
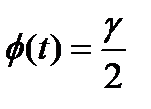
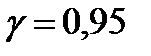 неизвестного математического ожидания
неизвестного математического ожидания 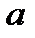 нормально распределенного количественного признака
нормально распределенного количественного признака 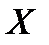 по выборочной средней
по выборочной средней 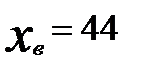 , генеральное среднее квадратическое отклонение
, генеральное среднее квадратическое отклонение 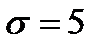 объем выборки равен 25.
объем выборки равен 25.
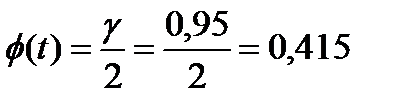
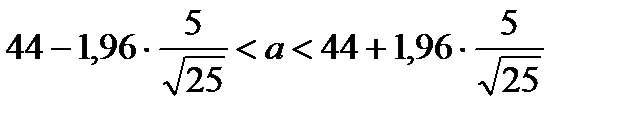
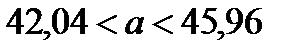
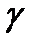 математического ожидания
математического ожидания 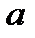 нормально распределенного количественного признака
нормально распределенного количественного признака 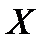 генеральной совокупности по выборочной средней и неизмененном среднем квадратическом отклонении и малом объеме выборки
генеральной совокупности по выборочной средней и неизмененном среднем квадратическом отклонении и малом объеме выборки 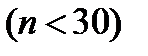 служит следующий интервал:
служит следующий интервал: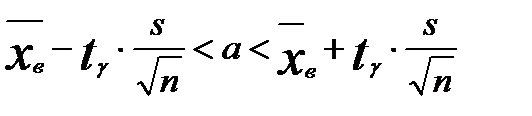
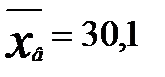
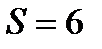 .
.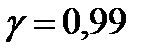 . Предусматривается, что величина распределена нормально.
. Предусматривается, что величина распределена нормально.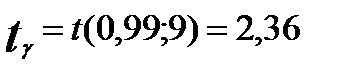
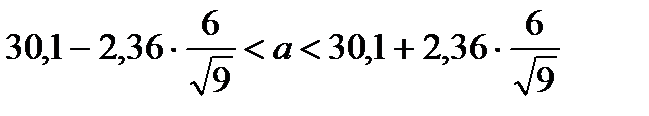
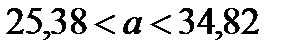
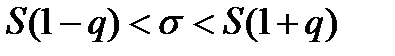 при q <1
при q <1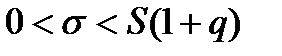 при q >1,
при q >1,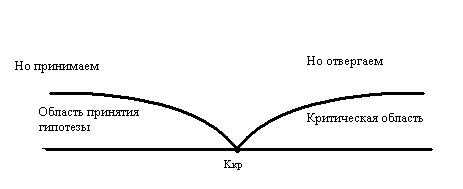
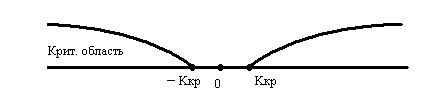 K < - K КР
K < - K КР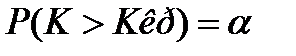
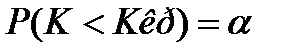

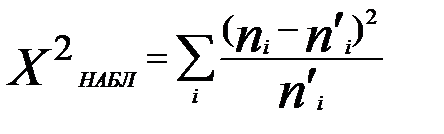
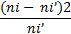

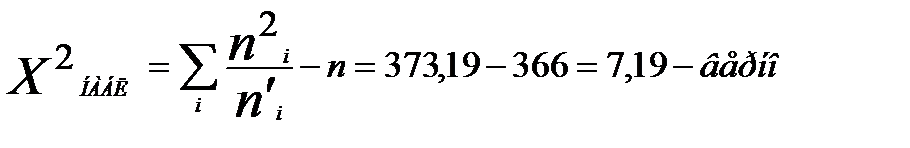
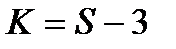 , где S-число различных вариант.
, где S-число различных вариант.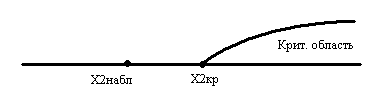
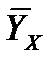 называется среднее арифметическое значение наблюдавшихся значений Y, соответствующих значению X = x.
называется среднее арифметическое значение наблюдавшихся значений Y, соответствующих значению X = x.
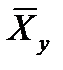 называется среднее арифметическое наблюдавшихся значений
называется среднее арифметическое наблюдавшихся значений  , соответствующих значению Y = y.
, соответствующих значению Y = y. - выборочное уравнение прямой регрессии Y на X;
- выборочное уравнение прямой регрессии Y на X;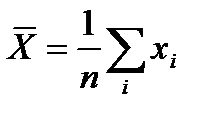 - среднее арифметическое значение X;
- среднее арифметическое значение X;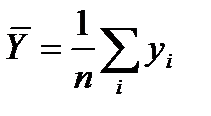 -среднее арифметическое значение Y;
-среднее арифметическое значение Y; ;
;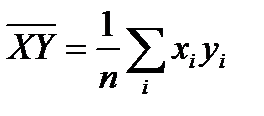 .
.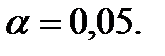
 координаты которых соответствуют значениям переменных X и Y.
координаты которых соответствуют значениям переменных X и Y.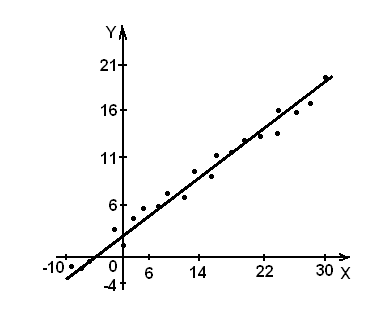
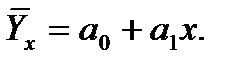
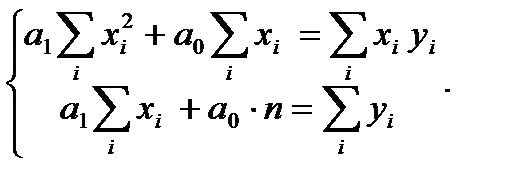

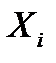

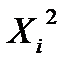

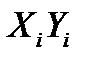
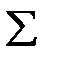
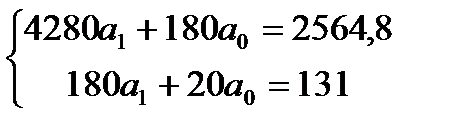
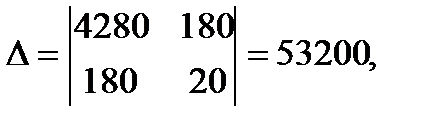
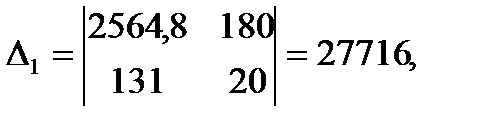
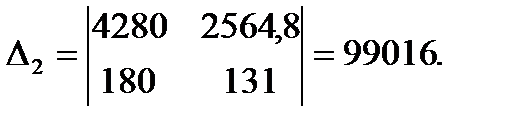
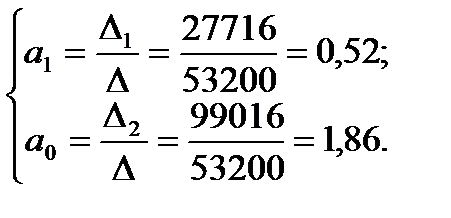
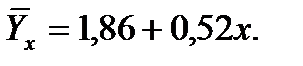

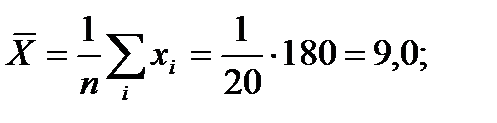
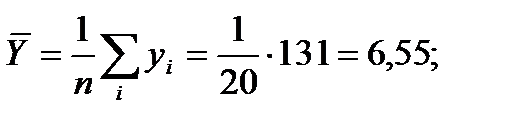
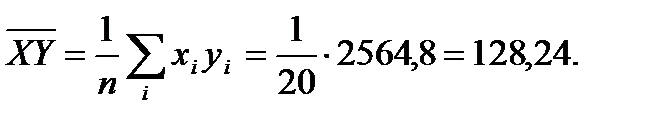
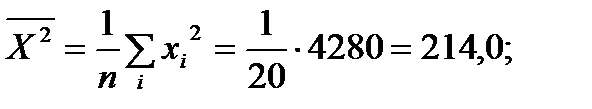
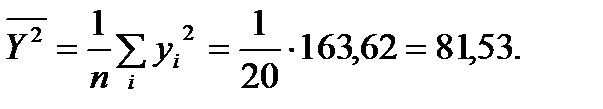
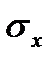 и
и 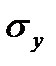 :
: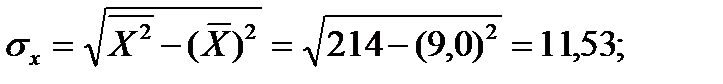


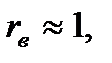 то между признаками связь очень тесная, близкая к линейной функциональной.
то между признаками связь очень тесная, близкая к линейной функциональной.
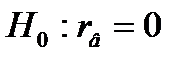 - переменная X не оказывает существенного влияния на Y.
- переменная X не оказывает существенного влияния на Y.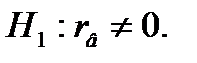
 Найдем наблюдаемое значение критерия
Найдем наблюдаемое значение критерия 
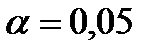 и числу степеней свободы
и числу степеней свободы 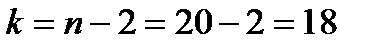 найдем критическую точку
найдем критическую точку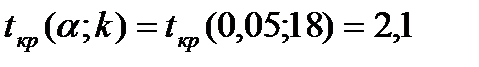 двусторонней критической области.
двусторонней критической области.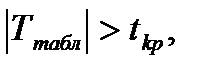 то нулевую гипотезу отвергаем.
то нулевую гипотезу отвергаем.


