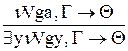Применение усиленной основной теоремы (2. 1) к новому доказательству непротиворечивости арифметики без полной индукции.

Арифметикой мы назовем (элементарную, т.е. не пользующуюся средством анализа) теорию натуральных чисел. Мы можем формализовать ее следующим образом, применяя наше логическое исчисление LK.

 

3.1. В арифметике обычно используются «функции», например, x’ (обозначает x+1), x+y, x*y.

Т.к. в наших логических исследованиях мы не вводим нескольких функциональных знаков, то для того, чтобы применить их результаты к арифметике, мы так формализуем арифметические высказывания, чтобы вместо функций в них фигурировали предикаты.

Например, вместо функции x’ мы используем предикат xVgy, который читается так: «x предшествует y», т.е. y=x+1. Далее, мы рассматриваем [x+y=z] как предикат с тремя аргументными местами, в котором каждый из знаков + и = в отдельности не имеет смысл. Другим предикатом является x=y; знак равенства здесь ничего общего со знаком равенства в [x+y=z].

Далее, число 1 мы не можем писать как обозначение некоторого объекта, т.к. мы в нашем формализме пользуемся только предикатными переменными и не имеем знаков для постоянных объектов. Мы поэтому вынуждены писать так: предикат «Sins x» содержательно означает «x есть число 1».

Предложение «x+1 следует за x» мы можем, например, представить в формализме так: "x"y"z ((Eins y & [x+y=z] É xVgz).

Остальные натуральные числа можно характеризовать предикатами

Eins x & x Vgy, Eins x & Vgy & y Vgz и т.д.

Как ни можно включить вводимые только что предикатные знаки в наше исчисление, в котором мы допускали ранее только переменные высказывания? Чтобы сделать это, мы просто условимся, что предикатные знаки будут рассматриваться точно также, как переменные высказывания.

Точнее, мы рассматриваем выражение вида

Eins x, xVgh, x=h, [x+h=z]

где x, h, z – обозначают некоторые предикатные переменные, лишь как более понятную запись формул

Ax, Bxh, Cxh, Dxhz.

В этом смысле следующие аксиомы действительно являются формулами в соответствии с нашими определением формулы.

(Число 1 нельзя рассматривать как обозначение некоторой предикатной переменной, т.к. в нашем исчислении предикатные переменные функционируют действительно как переменные, в то время как для переменных высказываний это не имеет смысла).

В качестве «аксиом» арифметики мы возьмем сначала приведенные ниже; позднее в связи с доказательством непротиворечивости (см. 3.3), мы укажем более общую точку зрения, в соответствии с которой можно будет строить новые допустимые аксиомы.

Равенство: "x (x=x)                   (рефлективность)       

    "x"y (x=y É y=x)                (симметричность)

    "x"y"z ((x=y & y=z) É x=z)        (транзитивность)

Единица: $x Eins x                             (существование 1)

    "x"y((Eins x & Eins y) É x=y) (единственность 1)

Предшественник: "x$y (x Vqy)             (существование следующего за)

     "x"y(x Vqy É ØEins y)                  (1 не имеет предшественника)

"x"y"z"u((xVgy & zVgu & x=z) É x=y) (единственность следующую за)

Формула B называется выводимой в арифметике без полной индукции, если существует LK-вывод секвенции

U₁,... U _m → B

где U₁,... U _m  - являются аксиомами арифметики.

Нельзя доказать, что это формальная арифметическая система дает возможность формализовать все обычные в содержательной арифметике доказательства (в которых не используется полная индукция), т.к. для содержательного изложения не существует точно очерченных рамок; нас может убеждать только часть отдельных содержательных доказательств.

 

3.2. Теперь мы докажем непротиворечивость описанной формальной системы. Сделать это с помощью усиленной основной теоремы (2.1) совсем просто.

3.2.1. «Противоречивая формула» U&ØU выводима в системе тогда и только тогда, когда имеется LK – вывод некоторой секвенции с пустым сукцедентом и арифметическими аксиомами в антецеденте.

Действительно, из Г→U & ØU можно получить Г→ так:

                                 U→U                 

                                                          NEA

                              ØU, U→               

                                                          UEA

                           U & ØU, U→ 

                                                          приставка

                           U, U & ØU→        

                                                          UEA

                     U & ØU, U & Ø U→

                                                          сокращение

Г→U & ØU                 U & ØU→

                                                                                             сечение

                       Г→

Обратное утверждение доказывается путем построения вывода, состоящего из единственного уточнения в сукцеденте.

Итак, если наша арифметика противоречива, то существует ZK-вывод с конечной секвенцией

U₁,... U _m →

где U₁,... U _m  являются арифметическими аксиомами.

3.2.2. Теперь мы применим усиление основной теоремы (2.1).

Арифметические аксиомы удовлетворяют условиям. Наложенными на S-формулы конечной секвенции в теореме 2.1. Следовательно, существует LK-вывод с той же коечной секвенцией, который имеет следующие особенности:

1) в него не входит сечение

2) в нем имеется некоторая H-секвенция, называемая «средней секвенцией», вывод которой не содержит знаков " и $ и из которых конечная секвенция получится с помощью следующих фигур заключения: AEA, EEA, уточнение, сокращение и перестановка в антецеденте.

Средняя секвенция имеет пустой сукцедент (2.1.1).

3.2.3. Затем мы переписываем свободные предметные переменные, как это делалось в III, 3.10, что не лишает вывод описанных выше особенностей и сообщает ему еще следующее свойство (III, 3.10.1): собственная переменная каждой ЕЕА входит в вывод только в секвенции, стоящие выше нижней секвенции этой ЕЕА.

3.2.4. После этого мы замещаем описываемым ниже способом каждую свободную предметную переменную везде, где она входит в вывод, одним и тем же натуральным числом. При этом получается некоторая фигура, которую мы уже не можем считать LK-выводом; в какой степени она все же имеет содержательный смысл, мы увидим позднее.

Замещение свободных предметных переменных числами производится в следующей последовательности:

3.2.4.1. Вначале заменяем числом 1 все свободные предметные переменные, не входящие в вывод в качестве собственной переменной какой-либо ЕЕА.

(Можно было бы взять любое другое число.)

3.24.2. Затем мы последовательно берем входящие в вывод фигуры заключения ЕЕА, начиная с самой нижней, и заменяем их собственные переменные (всюду, где они входят в “вывод”) числом, которое определяется следующим образом.

Фигура заключения ЕЕА может иметь лишь один из следующих двух видов:

 или

(на основании свойства подформульности 3, 2.5.1.3; V может быть только числом, в силу 3.24.1, 3.23).

В первом случае а заменяется на 1, во втором – на число, на 1 большее, чем v.

3.25. Теперь рассмотрим полученную из вывода фигуру. Нас в особенности интересует вид (бывшей) средней секвенции. О ней может сказать следующее:

Ее сукцедент пуст, а каждая из антецедентных d-формул имеет вид Eins 1 или вид vVgv¢, где v - некоторое число, v¢ - число, не большее, чем n, или, наконец, она получается из такой арифметической аксиомы, в начале которой стоят только знаки всеобщности, путем удаления этих знаков (и стоящих за ними связанных предметных переменных) и замены связанных предметных переменных в оставшейся части формулы числами.

(Все это следует из рассуждений, аналогичных тем, которые были проведены в 3, 2.5.1.2.)

Итак, S-формулы, стоящие в антецеденте средней секвенции, представляют содержательно истинные арифметические высказывания. Далее «вывод» средней секвенции получен из «вывода», не содержащего знаков " и $, в результате замены входящих в него свободных предметных переменных числами. Такой “вывод” содержательно представляет собой арифметическое доказательство, в котором использованы лишь правила вывода логики высказываний. Тем самым мы получаем следующий результат:

Если наша арифметика противоречива, то, пользуясь лишь истинными арифметическими высказываниями в применяя лишь правила вывода логики высказываний, можно доказать противоречие.

Используемые при этом «истинные арифметические высказывания» являются высказываниями вида Eins 1, vVgv¢ или численными частными случаями арифметических аксиом, начинающихся только знаками всеобщности, например, 3=3; 4=5É5=4; 3Vg4 É Eins 4.

То, что таких высказываний средствами логики высказываний не может быть выведено противоречие, почти очевидно, и доказательство этого может быть лишь формальным описанием содержательно ясного существа дела.

Поэтому мы не будем его проводить, а лишь укажем вкратце, как это обычно делают.

Устанавливают для всех числовых значений то, когда формулы Eins m, m=V, mVgv, m+v=r и т.д. истинны и когда они ложны. Далее обычным образом определяют истинность или ложность высказываний вида U&B, UÚB, U, UÉB как функций истинности или ложности их подформул.

После этого показывают, что все численные частные случаи аксиом являются “истинными”; а фигуры заключения логики высказываний приводят всегда от истинных формул только лишь к истинным формулам. Но формула, выражающая противоречие, не является истинной формулой.

 

3.3. Из заключений, сделанных в 3.2.5 легко указать, в каком направлении можно расширять систему арифметических аксиом так, чтобы из них не было выводимо противоречие:

мы можем допускать также аксиомы, в которых знаки всеобщности стоят лишь в начале и имеют областью действия всю основную часть формулы, в также такие, которые не содержат знака существования и для которых содержательно истинен каждый численный частный случай.

Например, можно допустить следующие аксиомы сложения:

"x"y(xVgyÉ[x+1=y]),

"x"y"z"u"v((xVgy&[z+x=u]&[z+y=v])ÉuVgv),

"x"y"z"u(([x+y=z]&[x+y=u])Éz=u),

"x"y"z([x+y=z]É[y+x=z]) и другие.

 

3.4. Т.к. полная индукция широко применяется в теории чисел, то арифметика без полной индукции имеет, конечно, лишь очень небольшое практическое значение. Однако для арифметики с полной индукцией до сих пор нет безупречного доказательства непротиворечивости.