
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Применение основной теоремы в логике высказываний.
1.1. Тривиальным следствием основной теоремы является уже давно известная непротиворечивость классической (и интуиционистской логики) предикатов: секвенция →(которая выводится из любой противоречивой секвенции→ U&U ср. 3.21) не может быть нижней секвенцией никакой фигуры заключения, кроме сечения, т.е. вообще не выводима.
1.2. Решение проблемы разрешения для интуиционистской логики высказываний. Используя основную теорию, мы можем получить простой способ решения для любой формулы логики высказываний, т.е. формулы без предметных переменных, вопросе о том, является ли она классической, а также интуиционистски истиной или нет. Секвенцию, в антецедент которой одна и та же формула не входит в качестве S-формулы более трех раз, мы назовем редуцированной. Имеет место следующая лемма. 1.2.1. Каждый LJ-вывод (LK-вывод), конечная секвенция которого является редуцированной, можно преобразовать в LJ-вывод (соответственно в LK-вывод) с той же конечной секвенцией, в которой все секвенции являются редуцированными (и который в случае, если первоначальный вывод не содержит сечения, тоже не содержит сечения). Доказательство. Назовем редукцией данной секвенции любую секвенцию, которая получается из данной в результате следующего преобразования: если в антецеденте или сукцеденте данной секвенции имеется несколько формально равных S-формул, мы вычеркиваем любые из них до тех пор, пока в антецеденте и независимо от этого останется тоже одна, две или три тоже S-формулы. Очевидно, что из одной редукции данной секвенции можно вывести любую другую редукцию этой секвенции с помощью уточнений, сокращений и перестановок, причем так, что будут использованы только редуцированные секвенции. После этого предварительного заключения мы проведем следующее преобразование данного LJ-вывода (соответственно LK-вывода). Все основные секвенции и конечная секвенция не изменяются; они все уже являются редуцированными. H-секвенции каждой из фигур заключения преобразуются в их редукции описанным выше способом. Ввиду сделанного заключения не имеет особого значения, если одинаковые секвенции в двух различных H-фигурах заключения заменяются при этом преобразовании различными редукциями, т.к. в этом случае одну из них легко вывести из другой с помощью уточнений, сокращений и приставок, получив в конце концов снова правильный вывод.
Преобразования фигур заключения производятся следующим образом. Если в Г некоторая формула входит более чем один раз, то она столько раз вычеркивается из Г в верхней и нижней секвенциях (на соответствующих местах), но входит после этого в Г только один раз. Тоже самое делается с ∆, Θ и Λ (т.е. с рядами формул, обозначенными так в схемах фигур заключения III, 1.2.1, 1.2.2). После описанных преобразований вывод состоит уже только из редуцированных секвенций. (Перестановка, в которой D равна C), представляет исключение, но она является тождественной фигурой заключения и ее можно вообще удалить). Данная лемма доказана. Из основной теоремы, дополнительной теоремы III (2.5.1.3) и вышеуказанной леммы следует: 1.2.2. Для каждой интуиционистски (классически) истинной редуцированной секвенции существует ее LJ-вывод (соответственно LK-вывод) без сечения, состоящий только из редуцированных секвенций, причем все H-S-формулы этого вывода являются подформулами S-формул этой секвенции. 1.2.3. Пусть тогда имеется некоторая секвенция без предметных переменных. Мы хотим решить вопрос о том, является ли она интуиционистски классически) истиной или нет. Прежде всего, вместо нее мы можем взять эквивалентную ей редуцированную секвенцию, которую мы обозначим посредством σ Очевидно, что число всех редуцированных секвенций, S-формулы которых являются подформулами S-формул секвенции σ Берем упомянутую конечную систему секвенций и выясняем сначала, какие из них являются основными секвенциями; такие секвенции выводимы. Относительно каждой из них по очереди выясняем, существуют ли такая фигура заключения, для которой она может являться нижней секвенцией, в то время как верхними секвенциями (одной или двумя) являются какие-либо из секвенций, выводимость которых уже установлена. Если окажется, что такая фигура заключения существует, то исследуемая секвенция присоединяется к выведенным. (Все это, очевидно, разрешимо). Так мы продолжаем до тех пор, пока или сама секвенция σ
В последнем случае согласно 1.2.2 секвенция σ Этот вопрос о ее истинности решен.
1.3. Новое доказательство невыводимости закона исключенного третьего в интуиционистской логике. Разрешающей процедуре можно придать другой, гораздо более удобный для практических применений вид. Приведенной выше (1.2) описание такой процедуры предназначалось лишь для того, чтобы показать принципиальную возможность решения проблемы. В качестве примера мы докажем невыводимость закона исключенного третьего в интуиционистской логике способом, не зависящим от описанной выше разрешающей процедуры. Секвенция, о которой идет речь →A Предположим, что существует LJ-вывод этой секвенции. Тогда согласно основной теореме существует ее вывод без сечения. Самой нижней фигурой заключения этого вывода может быть лишь OES, т.к. во всех остальных LJ-фигурах заключения их антецедент нижней секвенции непуст или в сукцеденте стоит формула с отличным от V высшим знаком. Правда, рассматриваемая секвенция может быть нижней секвенцией уточнения в сукцеденте, но тогда верхней секвенции этой фигуры заключения была бы секвенция →, а последняя невыводима согласно 1.1. Итак, должна быть выводима (без сечения) одна из следующих секвенций: →A или →A. (Такое допущение, вообще, приводит к следующему заключению: если U Но секвенция A, вообще не может быть никакой секвенцией какой-либо LJ-фигуры заключения (кроме сечения), за исключением опять-таки уточнения в сукцеденте с верхней секвенцией →, т.к. →A, кроме того, не является и основной секвенцией, то она не выводима. Секвенция → A может быть выведена только с помощью NES из секвенции A →, которая, ввиду того, что A не имеет внешнего знака, может бут выведена лишь из секвенции A, A →. Продолжая так, мы будем получать лишь секвенции вида А,...,А →, но никогда не придем к основной секвенции. Итак, А
|
||||||
|
Последнее изменение этой страницы: 2021-04-12; просмотров: 50; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.162.179 (0.009 с.) |
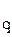 .
. , конечно. Поэтому разрешаемую процедуру можно осуществить так.
, конечно. Поэтому разрешаемую процедуру можно осуществить так. будет отнесена к выводимым, или окажется, что описанная процедура уже не дает никаких новых выводимых секвенций.
будет отнесена к выводимым, или окажется, что описанная процедура уже не дает никаких новых выводимых секвенций.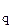 вообще невыводима в соответствующем исчислении (LJ или соответственно LK).
вообще невыводима в соответствующем исчислении (LJ или соответственно LK).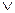 A. (где A – переменное высказывание, а не обозначение произвольной формулы).
A. (где A – переменное высказывание, а не обозначение произвольной формулы).


