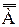Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Равночисленность множеств (равномощность).Стр 1 из 22Следующая ⇒
Кардинальные числа. Часто вместо выражения «равночисленность множеств» используются также выражения «эквивалентность множеств» или «имеют одинаковую мощность». Понятия, которые мы определим в этом параграфе, относятся к важнейшим и самым основным понятиям теории множеств. Определение7.1. X~RY ≡ R Выражение X~RYсчитается: отношение R устанавливает равночисленность множеств Х и Y. Отношение: x R1 y ≡ x =2y устанавливает, таким образом, равночисленность множества всех натуральных чисел и множества всех положительных четных чисел; отношение xR2y≡x=y2 устанавливает равночисленность множества всех натуральных чисел и множества всех квадратов натуральных чисел. Множества Х и Y называются равномощными, если между ними можно установить взаимно-односвязные соответствия (Шиханович, стр.198), взаимно-односвязное соответствие означает: a) элемент х b) каждый элемент обоих множеств попал в одну и только одну пару áx,yñ. Например, если Х − множество всех юношей на танцплощадке, а Y – множество всех девушек на танцплощадке, то пары áx,yñ образуют танцующих друг с другом юношей и девушек. Два конечных множества равномощны тогда и только тогда, когда они содержат одинаковое количество элементов. Поэтому понятие равномощность является обобщением на бесконечные (или на произвольные) множества понятия равночисленности конечных множеств. 1, 2, 3, … n – множество N. ↓ ↓ ↓ ↓ 2, 4, 6, … 2n − множество четных чисел. Множество натуральных чисел (N) содержит столько же элементов, сколько и его часть − множество четных чисел. Точно также устанавливается взаимнооднозначное соответствие между множеством N и множеством всех квадратов натуральных чисел: n → n2; и множество всех кубов натуральных чисел: n → n3 и т. д. Вообще между множеством N и любой его бесконечной частью всегда можно установить взаимнооднозначное соответствие. Для этого достаточно перенумеровать по порядку числа из этой части. Пусть К1 и К2 две концентрические окружности. Точке К1 мы приводим в соответствие точку окружности К2, если эти точки лежат на полупрямой, выходящей из общего центра О1. Данное соответствие устанавливает равночисленность множества точек, лежащих на этих окружностях.
К2 О1 А1 А2 А В В1 В2 Примеры равночисленности точек: «где больше точек, на отрезке равном 1 см или 1 м?». На этих отрезках точек поровну! То есть часть равна целому. Этим свойством могут обладать только бесконечные множества. Из теоремы 5.2, определения 7.1 (áx,yñ Следствие 6.5. R Следствие 6.4. a) x b) x с)R Следствие 7.1. Отношение R устанавливает равночисленность множеств X и Y тогда, и только тогда, когда множеству Определение7.2. X~Y ≡ Выражение X~Y читается: множества X и Y равночисленны. Таким образом, два множества равночисленны тогда, и только тогда, когда существует отношение, устанавливающее их равночисленность. Очевидно, что два конечных множества равночисленны тогда, и только тогда, когда число элементов одного из них равно числу элементов другого. В рассуждениях этого параграфа будет удобно обозначать отношение тождества символом J. Таким образом, вместо x=y будем писать xJy. Такая символика достаточно часто применяется в логике. Заметим еще, что xJx есть логическая теорема. Лемма7.1. X = J (X) [X = R (X)] Доказательство. (1.1) y (1.2) y (1.3) (1.4) y (2.1) y (2.2)
(2.3) x1 (2.4) x1Jy {2.2} (2.5) y X = J (X) {определение 1.1, 1.1 → 1.4, 2.1 → 2.5} Теорема 7.1. a) X~X (рефлективность) b) X~Y→Y~X (симметричность) с) X~Y Эту теорему словесно можно сформулировать так: отношение равночисленности множеств рефлексивно, симметрично и транзитивно, а потому оно есть отношение эквивалентности. Доказательство (a): (1) J (2) J-1 (3) J (4) Jx (5) x (6) Dℓ(J) =1 {определение 1.1 − (x=y= (7) xÌDℓ(J) {теорема 1.1 − (xÌ1), 6} (8) Dℓ(Jx) = Dp (Jx) = x {лемма 6.5a, b, 7, 7.1 − (x = J(x))} (9) X ~ X ~ X {определение 7.2 − (X ~ Y ≡ X ~ RY), 9} Доказательство (b): (1) X ~ Y {доп.} (2) X ~ R1Y {определение 7.2, 1} (3) R1 (4) X = Dℓ (R1) (5) R1-1 (6) Dℓ (R1-1) = Y (7) Y ~ R-1 X {определение 7.1, 5, 6} Y ~ X {определение 7.2, 7} Доказательство (c): (1) X ~ Y (2) X ~ R1Y (3) R1, S1 (4) X = Dℓ (R1) (5) R1; S1 (6) X = Dℓ (R1; S1) (7) X ~ R1; S1 Z {определение 7.1, 5, 6} X ~ Z {определение 7.2, 7} Следующими двумя леммами будем пользоваться в одном из дальнейших параграфов. Лемма 7.2. X ~ RY → Y = R (x) Доказательство. (1) X ~ RY {доп.} (2) X = Dℓ (R) {определение 7.1, 1} (3) Y = Dp (R) {определение 7.1, 1} (4) Dp (Rx) = R (x) {лемма 6.5b − (x (5) Rx = R {лемма 6.8 − (X = Dℓ (R) → Rx = R), 2} (6) Dp (Rx) = Dp (R) {5} Y = R (x) {3, 6, 4} Лемма 7.3. R Доказательство. (1) R (2) X (3) Rx (4) Dℓ (Rx) = X {лемма 6.5a − (x (5) Dp (Rx) = R (x) {лемма 6.5b − (x X ~ Rx R (x) {определение 7.1 − (X~RY ≡R Мы вводим новое исходное понятие − понятие мощности множества. Мощность множества X обозначается через
Аксиома 7.1. Замечание 7.1. Будем считать, что мощность пустого множества есть число нуль, а мощность конечного множества − натуральное число, указывающее, сколько элементов насчитывает данное множество. Таким образом, мощности двух множеств тождественны тогда, и только тогда, когда эти множества равночисленны. (В математической терминологии утвердить название «мощность множества», хотя, возможно, лучше было бы пользоваться термином «численность множества»). Заметим, что из аксиомы 7.1 и из рефлективности, симметричности и транзитивности тождества непосредственно следует теорема 7.1. Определение 7.3 . Выражение m Теорема 7.2. а) b) c) Эта теорема имеет следующую словесную формулировку: a. Мощность произвольного множества есть кардинальное число. b. Для всякого множества существует точно одно кардинальное число, равное мощности этого множества. c. Для всякого кардинального числа существует множество мощность которого равна данному кардинальному числу. Лемма 7.4. Для любых множеств А и В существуют множества А1 и В1, такие, что А1~A, В1~В и А1 Доказательство. Множества А1 и В1 мы определяем следующим образом: á1, añ á2, bñ Легко видеть, что А1 и В1 удовлетворяют условию леммы. В рассуждениях о кардинальных числах безразлично, какое из рассматриваемых равночисленных множеств мы примем во внимание. По лемме 7.4мы можем всегда данные два множества заменить непересекающиеся множествами. Лемма 7.5. a) A~B b) A~B Доказательство. a. Допустим, что отношение R устанавливает равночисленность множеств А и В, а отношение R1 − равночисленность А1 и В1. Нетрудно видеть, что отношение S, определяемое формулой:
xSy ≡ (xRy устанавливает равночисленность множеств А+А1 и В+В1.
________________________ * – Такое определенное отношение S называется суммой отношения R, R1 и обычно обозначается через R+R1. Произведение и дополнение отношений определяются следующим образом: xR∙Sy ≡ xRy xR’y ≡ ~(xRy). Можно показать, что определяемые операции над отношениями удовлетворяют аксиомам алгебры Буля, приведенным в §3. Тем самым мы получаем еще одну интерпретацию этой алгебры. Заметим, что условие: множества А и А1, а также В и В1 не пересекаются существенно, как можно видеть из следующего примера: А={1, 2, 3}, A1={1, 2, 3, 4} B={1, 2, 3}, B1={1, 4, 5, 6} b. Самостоятельно. Леммами 7.4, 7.5будет показываться в следующем параграфе. Заметим еще, что мощность множества всех натуральных чисел обозначается через Таким образом, имеют место равенства: Натуральные числа: Действительные числа: Множества, мощность которых есть число
Множество А называют несчетным, если оно бесконечно и несчетно. Из теоремы Кантора (Шиханович, 199) следует, что сегмент [0, 1] несчетен. Очевидно, любое множество либо не более чем счетно, либо несчетно. Множество А называют не более чем счетным, если А конечно (в частности, пусто) или счетно. Среди несчетных множеств важнейшее значение имеют континуальные множества. Множество А называют континуальным, если А и [0, 1] равномощны. Множество действительных чисел (D) континуально. Каждое действительное число можно записать в виде бесконечной десятичной дроби вида а, α1, α2, …, αn (0,50000…, 0,49999…, 0,575675…). Из теоремы Кантора следует, что любое континуальное множество несчетно. Определение 7.4. Множество А есть запас последовательности
Таким образом, необходимым и достаточным условием счетности множества А является существование бесконечной последовательности, не имеющей повторяющихся членов, запас которой есть множество А. Доказательство. Пусть а1, а2, а3, … бесконечная последовательность, не имеющая повторяющихся членов, запас которой – множество А. Приведем в соответствие каждому члену этой последовательности его индекс, т.е. члену а1 – число 1, члену а2 – число 2 и т.п. Легко видеть, что данное соответствие устанавливает эквивалентность множеств А и N. Отсюда следует доказываемая теорема. Нужно заметить, что почти для всех теорем о мощностях существуют эквивалентные им теоремы, в которые входит не это понятие, а понятие равно численности множеств. Т.о., исключение понятия мощности множества из перечня исходных понятий теорем множеств (очевидно, одновременно нужно было бы исключить и аксиому 7.1) не привело бы к существенному обеднению этой теории, но вызвало бы значительные трудности в формулировке многих ее теорем.
|
|||||||||
|
Последнее изменение этой страницы: 2021-04-12; просмотров: 442; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.95.38 (0.076 с.) |
 1–1
1–1  X = Dℓ (R)
X = Dℓ (R) 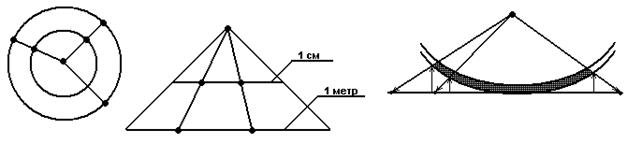 К1 О1 О1
К1 О1 О1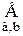 Ф(a,b)≡Ф(x,y)), и следствий 6.5 и 6.3 следует следствие 7.1.
Ф(a,b)≡Ф(x,y)), и следствий 6.5 и 6.3 следует следствие 7.1.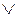 áx,yñ, áx,zñ
áx,yñ, áx,zñ 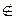 Ea,b a R b];
Ea,b a R b];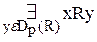
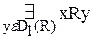
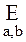 (a R b) не принадлежат никакие две (различные) упорядоченные пары, первые или вторые элементы которых тождественны, причем первые элементы упорядоченных пар, принадлежащих множеству
(a R b) не принадлежат никакие две (различные) упорядоченные пары, первые или вторые элементы которых тождественны, причем первые элементы упорядоченных пар, принадлежащих множеству  X~ RY
X~ RY xJy {1.2}
xJy {1.2}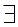 xRy, x
xRy, x 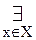 xJy {определение 6.4, 2.1}
xJy {определение 6.4, 2.1}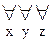 [xRy
[xRy 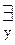 xRy)}
xRy)}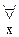 (x
(x 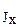 X {определение 7.1 − (X~RY ≡ R
X {определение 7.1 − (X~RY ≡ R 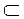 Dℓ (R) → Dp (Rx) = R (x))};
Dℓ (R) → Dp (Rx) = R (x))};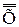 . Создатель теории множеств Г. Кантор считал, что мы приходим к понятию мощности множества, отвлекаясь от того, какие предметы образуют данное множество и как эти предметы в нем упорядочены. Две черточки в обозначении мощности множества и должны, собственно, символизировать эту двойную абстракцию. К системе теории множеств мы присоединяем новую аксиому, в которую входит введенный исходный термин:
. Создатель теории множеств Г. Кантор считал, что мы приходим к понятию мощности множества, отвлекаясь от того, какие предметы образуют данное множество и как эти предметы в нем упорядочены. Две черточки в обозначении мощности множества и должны, собственно, символизировать эту двойную абстракцию. К системе теории множеств мы присоединяем новую аксиому, в которую входит введенный исходный термин: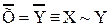
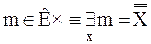
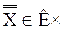
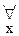
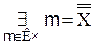
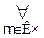
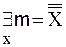
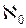 (читается: алеф-нуль − еврейский алфавит − ввел Г. Кантор), мощность множества всех действительных чисел − через f.
(читается: алеф-нуль − еврейский алфавит − ввел Г. Кантор), мощность множества всех действительных чисел − через f.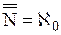
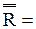 f
f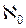 , называются счетными, то есть все множества, которые имеют столько же элементов, сколько имеет множество натуральных чисел, называются счетными. Иными словами, множества называется счетным, если оно бесконечно, но его элементы можно перенумеровать натуральными номерами (четные числа, нечетные, простые, да и вообще любая бесконечная часть множества натуральных чисел являются счетными множествами).
, называются счетными, то есть все множества, которые имеют столько же элементов, сколько имеет множество натуральных чисел, называются счетными. Иными словами, множества называется счетным, если оно бесконечно, но его элементы можно перенумеровать натуральными номерами (четные числа, нечетные, простые, да и вообще любая бесконечная часть множества натуральных чисел являются счетными множествами).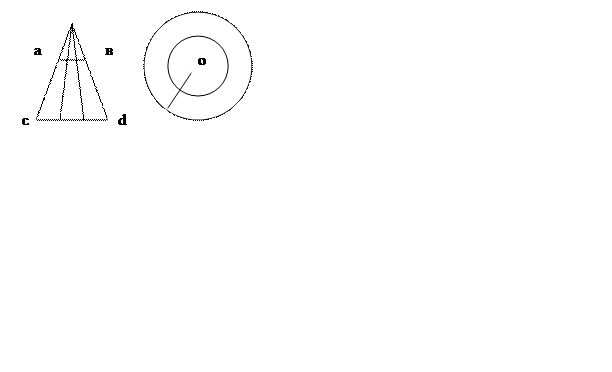 Множества, мощность которых есть число f, называют множествами континуума.
Множества, мощность которых есть число f, называют множествами континуума.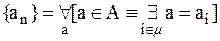
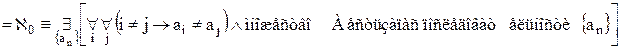 Теорема 7.3.
Теорема 7.3.