
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Общая схема метода Гаусса для систем, имеющих единственное решение
Пусть Получим
где Умножим разрешающее уравнение (4) на
где Если какой-либо из коэффициентов (То есть если в какой-либо из уравнений отсутствовала переменная
где
Продолжая аналогичные вычисления, приведем систему (3) к эквивалентной системе с треугольной матрицей коэффициентов
Прямой ход решения выполнен. Обратный ход: a) последовательно исключаем неизвестное
Затем исключаем неизвестное
В результате получаем решение системы
Для уменьшения погрешности вычислений существуют различные модификации метода Гаусса. Метод Гаусса с выбором максимального элемента по столбцу В начале первого шага прямого хода среди коэффициентов В начале второго шага прямого хода максимальный по модулю элемент выбранный среди коэффициентов При выполнении процедуры прямого хода возможны следующие случаи: 1. матрица А приводится к треугольной (получаю решение). 2. число преобразованных уравнений системы меньше числа неизвестных (ранг матрицы А< n) – Это происходит, если в системе получаются в процессе преобразований тождества 0=0. Система имеет бесконечное множество решений.
3. все коэффициенты при неизвестных в каком-либо уравнении равны нулю, свободный член отличен от нуля. Система не имеет решения.
Блок-схема решения системы линейных алгебраических уравнений методом Гаусса с выбором главного элемента (по столбцу)
ЛЕКЦИЯ 4
Метод итераций Рассмотрим систему линейных алгебраических уравнений
Если все диагональные элементы
где
Введем обозначения
Тогда система (2) запишется в виде
В качестве начального приближения
.........
Если существует предел x последовательности векторов
Достаточное условие сходимости итерационного процесса: Теорема. Если какая-нибудь норма матрицы А меньше единицы: Под нормой матрицы
Пример: для матрицы
В расчетах полагают
где
Из неравенства (5) можно получить оценку числа итераций k, необходимых для обеспечения заданной точности e. Отклонение приближения
Для вывода (6) достаточно рассмотреть равенства:
Далее И, учитывая, что В неравенствах (5) и (6) используются согласованные нормы для матриц и векторов, т.е. m и l-нормы. Неравенство (6) дает завышенную оценку числа итераций k. Из (6) можно получить удобное условие, позволяющее принять приближение
Пример: Найти решение системы уравнений
методом итераций с точностью 10-2. Решение: Приведем систему к виду (2)
Запишем последовательность итераций
Для приведенной матрицы В качестве начального приближения возьмем вектор-столбец свободных членов приведенной системы Число итераций для достижения заданной точности
Вычислим теперь три последовательных приближения по формулам (8) и оценим погрешность каждого результата, используя неравенство (6) в виде:
Первое приближение:
Следовательно, Далее последовательно находим:
Третья итерация:
Заданная точность достигается за 5 шагов. Точное решение
|
||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 106; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.163.58 (0.027 с.) |
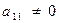 . (В противном случае в качестве первого уравнения возьмем какое-либо другое). Разделим первое уравнение на
. (В противном случае в качестве первого уравнения возьмем какое-либо другое). Разделим первое уравнение на 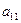 .
.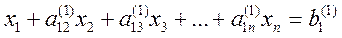 , (4)
, (4)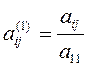 ;
; 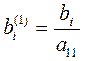
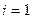 ,
, 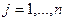
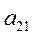 и вычтем полученное уравнение из второго уравнения системы (3). Аналогично преобразуем остальные уравнения. Система примет вид
и вычтем полученное уравнение из второго уравнения системы (3). Аналогично преобразуем остальные уравнения. Система примет вид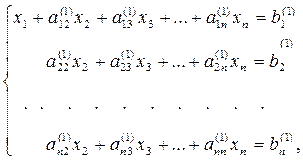 (5)
(5)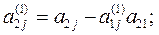
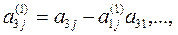
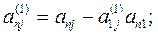
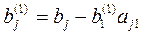
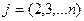
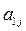 окажется равным нулю, то j-ое уравнение системы (3) войдет в систему (5) без изменений т.е.
окажется равным нулю, то j-ое уравнение системы (3) войдет в систему (5) без изменений т.е.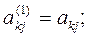
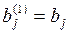
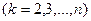
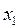 , то уравнение не преобразуется). Теперь, оставив без изменения первое уравнение системы (5), сделаем разрешающим второе уравнение и применим описанную процедуру к системе из n-1 уравнений, исключая
, то уравнение не преобразуется). Теперь, оставив без изменения первое уравнение системы (5), сделаем разрешающим второе уравнение и применим описанную процедуру к системе из n-1 уравнений, исключая 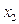 из оставшихся уравнений. Получим систему
из оставшихся уравнений. Получим систему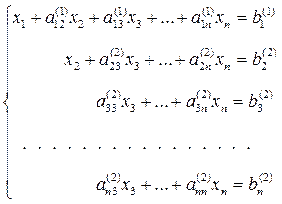
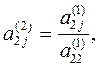
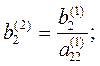
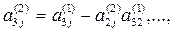
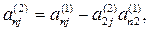
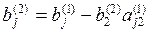
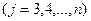
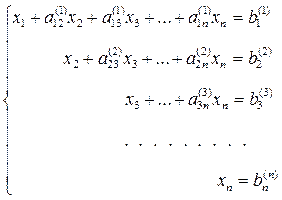 (6)
(6)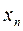 , начиная с
, начиная с 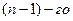 уравнения и заканчивая первым. Получаем
уравнения и заканчивая первым. Получаем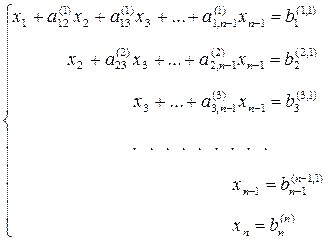 (7)
(7)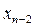 из уравнений с номером j
из уравнений с номером j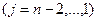 и т.д.
и т.д.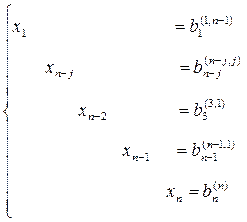
 при неизвестном
при неизвестном 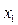 находят наибольший по модулю. Пусть это
находят наибольший по модулю. Пусть это 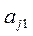 . После этого в исходной системе делают перестановку: меняют местами 1-ое и j-ое уравнения. Далее выполняют описанные действия.
. После этого в исходной системе делают перестановку: меняют местами 1-ое и j-ое уравнения. Далее выполняют описанные действия.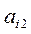
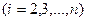 при неизвестном
при неизвестном 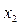 . Снова возможна перестановка уравнений и исключение
. Снова возможна перестановка уравнений и исключение 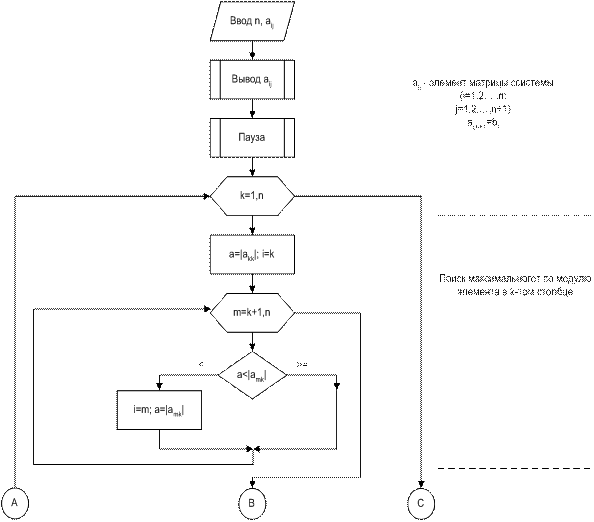
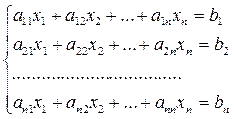 (1)
(1)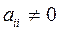
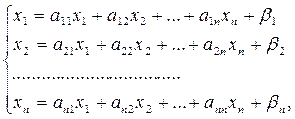 (2)
(2)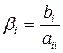
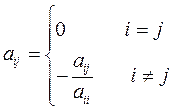
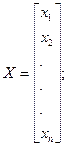
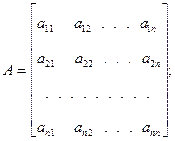
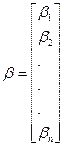
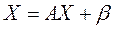 (3)
(3)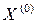 возьмем вектор b и подставим его в уравнение (3). Получим
возьмем вектор b и подставим его в уравнение (3). Получим 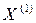 .Продолжая процесс, получим последовательности приближений:
.Продолжая процесс, получим последовательности приближений: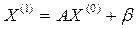 - первое приближение
- первое приближение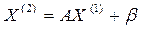 -второе приближение (4)
-второе приближение (4)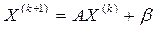 - (k+1)-ое приближение.
- (k+1)-ое приближение.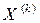 то, переходя к пределу в равенстве
то, переходя к пределу в равенстве 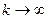 , убеждаемся, что x является решением уравнения (3), т.е.
, убеждаемся, что x является решением уравнения (3), т.е.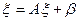
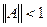 , то уравнение (3) имеет единственное решение x, к которому стремится последовательность итераций (4) при любом выборе начального приближения.
, то уравнение (3) имеет единственное решение x, к которому стремится последовательность итераций (4) при любом выборе начального приближения.
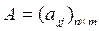 понимают следующие выражения:
понимают следующие выражения: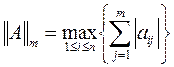 (m – норма - максимальное значение суммы модулей элементов строки)
(m – норма - максимальное значение суммы модулей элементов строки) (l – норма - максимальное значение суммы модулей элементов столбца)
(l – норма - максимальное значение суммы модулей элементов столбца) (k - норма)
(k - норма)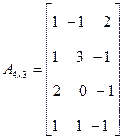
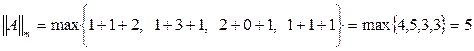
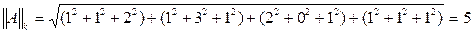
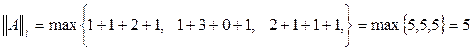
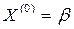 . Погрешности приближенного решения уравнения (3) на k-м шаге оценивают неравенством
. Погрешности приближенного решения уравнения (3) на k-м шаге оценивают неравенством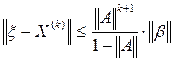 , (5)
, (5)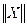 - норма вектора X
- норма вектора X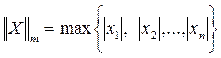 m-норма или кубическая норма
m-норма или кубическая норма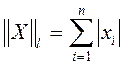 l-норма или октаэдрическая норма
l-норма или октаэдрическая норма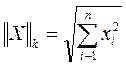 k-норма или сферическая норма.
k-норма или сферическая норма.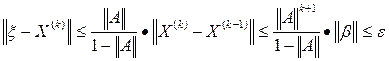 (6)
(6)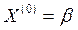 ;
; 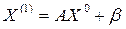 ;
; 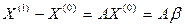 ;
;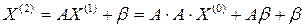 ;
;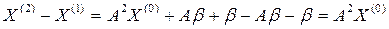 ; и т.д.
; и т.д.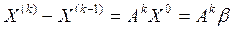
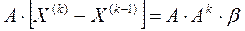 .
.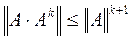 , т.к. норма
, т.к. норма 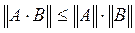 .
.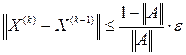 (7)
(7)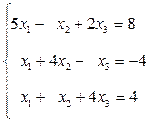
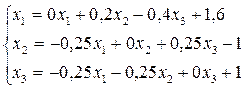
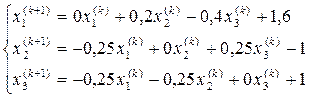 (8)
(8)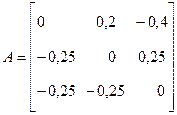 достаточное условие сходимости выполняется по m-норме:
достаточное условие сходимости выполняется по m-норме: 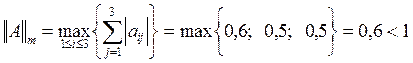
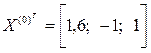 .
.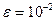 определяем из неравенства (6)
определяем из неравенства (6) 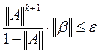 , которое запишем так:
, которое запишем так: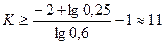 , действительно:
, действительно: 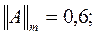
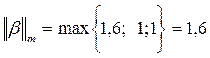 .
.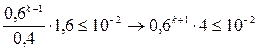 ;
; 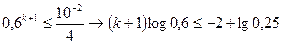 т.к.
т.к. 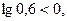 то
то 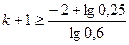 ;
; 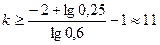 .
.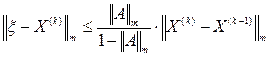 .
. 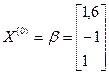
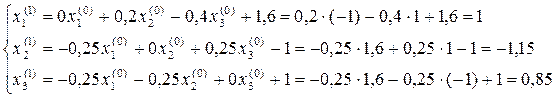
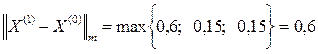
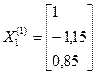 дает значение корня ξ с погрешностью, не превышающей величины
дает значение корня ξ с погрешностью, не превышающей величины 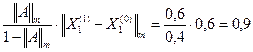 .
.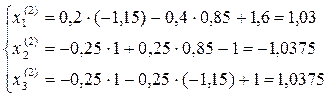
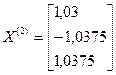 ;
; 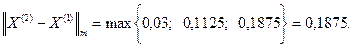
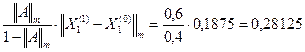 .
.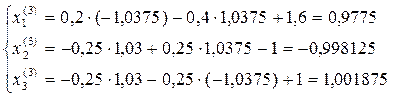
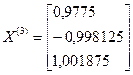 ;
; 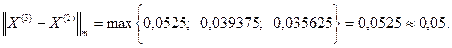
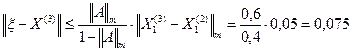 .
.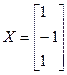 .
.


