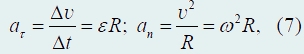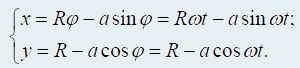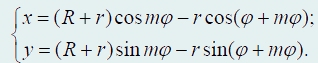Движение материальной точки по произвольной кривой

Если угловая скорость не является постоянной, то имеет смысл ввести понятие углового ускорения, которое мы обозначим греческой буквой ε (эпсилон).

Угловым ускорением называется отношение изменения угловой скорости к промежутку времени, в течение которого это изменение произошло, при промежутке времени, стремящемся к нулю:

 

Используя связь между линейной и угловой скоростями, эту формулу можно переписать в виде

 

 

Заметим, что в данном выражении в числителе стоит изменение модуля скорости (а не вектора скорости!). Полное же ускорение — отношение изменения вектора скорости к промежутку времени, таким образом, оказывается состоящим из двух частей, одна из которых описывает изменение направления вектора скорости (это ускорение является центростремительным, или нормальным¹), а вторая − изменение модуля скорости (это ускорение называется касательным, или тангенциальным).

Если направление вектора скорости не изменяется, то вектор ускорения направлен вдоль той же прямой, что и скорость. Поэтому следует считать, что вектор тангенциального ускорения совпадает с направлением вектора скорости, если скорость возрастает, и противоположен ему, если величина скорости убывает.

При движении материальной точки по произвольной кривой малый участок траектории можно приближенно заменить небольшой дугой окружности. Для этого следует воспользоваться следующим способом построения такой окружности, который аналогичен построению касательной прямой. Напомним, что касательную можно считать предельным положением секущей прямой.

Возьмем слева и справа от точки А две точки − А^/, А^//, лежащие на заданной линии (рис. 75).

 

 

рис. 75

 

Проведем через эти три точки окружности секущую С^/ (если три точки лежат на одной прямой, то будем считать эту прямую окружностью очень большого радиуса). После этого начнем мысленно приближать точки А^/, А^// к точке А, соответственно изменяя секущую окружность. При стремлении точек А^/, А^// к точке А секущая окружность будет стремиться к предельному положению С_o. Эта предельная окружность называется соприкасающейся в точке А, ее радиус называется радиусом кривизны линии в данной точке, а центр − центром кривизны.

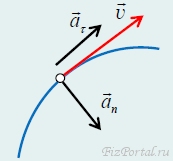
Таким образом, движение по произвольной кривой на малом участке можно рассматривать как движение по соприкасающейся окружности.

Вектор скорости v частицы всегда направлен по касательной к линии траектории движения, а вектор ускорения можно разложить на две составляющие (рис. 76):

 

 

рис. 76

 

одна из них, тангенциальное ускорение а_τ, описывает изменение модуля скорости и направлена по касательной к траектории, а другая, нормальное ускорение а_n, описывает изменение направления вектора скорости и направлена перпендикулярно касательной (по нормали) к центру кривизны траектории (в сторону ее вогнутости). Модули этих компонент ускорений рассчитываются по формулам

 

 

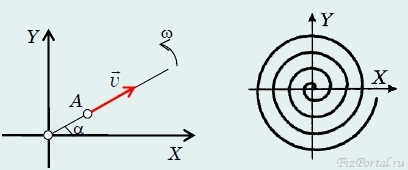
где R − радиус кривизны траектории в данной точке. Сумма векторов ускорений  а_τ, и а_n является вектором полного ускорения а. Конечно, вектор полного ускорения можно представить в виде суммы проекций а_x и а_y на произвольно выбранные оси координат (рис. 77).

 

 

рис. 77

Но разложение вектора на нормальную и  тангенциальную составляющие имеет два существенных преимущества: первое − обе компоненты а_τ и а_n имеют явный физический смысл; второе − такое разложение «привязывается» не к произвольно выбранной системе координат, а непосредственно к траектории движения и вектору скорости.

¹Название «нормальное» происходит от математического термина «нормаль», то есть перпендикуляр.

Суперпозиция движений

Мы изучили несколько простейших моделей движения. Сейчас постараемся показать, как из этих простых движений можно «конструировать» более сложные и красивые движения. Слово «суперпозиция» обозначает сложение, наложение, сочетание, оно очень часто используется в физике.

 

 

Возможность такого наложения различных видов движения обусловлена возможностью описывать его в различных системах отсчета и переходить из одной системы в другую по формулам

 

 

Теперь мы можем независимо задавать закон движения в подвижной системе отсчета r^/(t), закон движения самой движущейся системы r_o(t) и получать более сложный закон движения. Далее может быть, что и неподвижная система отсчета движется относительно другой, еще более неподвижной системы. Тем самым добавляется еще одно слагаемое и т. д. На этом пути открываются практически неограниченные возможности. Рассмотреть их всех невозможно, поэтому мы вынуждены ограничиться несколькими простыми, но красивыми движениями.

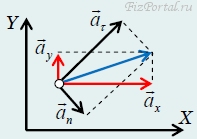
Движение тела, брошенного под углом к горизонту, можно представить в виде суперпозиции равномерного движения вдоль горизонтальной оси и равноускоренного движения вдоль вертикальной оси. Такой «суперпозиции» можно придать наглядный смысл: пусть в вагоне равномерно и прямолинейно движущегося поезда вверх подброшен небольшой шарик. В системе отсчета, связанной с вагоном, шарик движется вдоль вертикальной прямой с постоянным ускорением свободного падения. А в системе отсчета, связанной с землей, движение шарика будет движением по описанной ранее параболе. Отметим также, что «разложение движения на составляющие» не является однозначным¹. Так, то же движение тела, брошенного под углом к горизонту, можно представить в виде «суммы» равномерного движения вдоль прямой, направленной под углом к горизонту, задаваемой вектором начальной скорости, и равноускоренного движения вдоль вертикальной прямой. Фактически эти разложения мы использовали ранее при описании этого движения.

Суперпозиция вращательного и поступательного движений. Пусть материальная точка А движется по прямому стержню с постоянной скоростью v, а стержень вращается вокруг оси с постоянной угловой скоростью ω. Совместим начало системы отсчета с осью вращения (рис. 79).

 

 

рис. 79

 

Тогда расстояние от точки А до начала отсчета и угол поворота стержня зависят от времени по законам

 

l = vt, α = ωt.

 

 

Зависимость декартовых координат точки от времени имеет вид

 

х = lcosα = vtcosωt;

 

х = lsinα = vtsinωt.

 

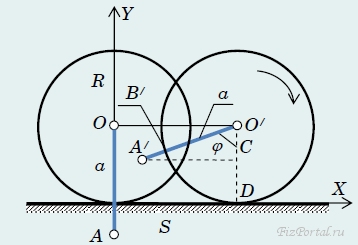
и описывает движение по спирали. Еще одна суперпозиция поступательного и вращательного движений. Пусть колесо радиуса R катится по горизонтальной поверхности без проскальзывания. Точка А расположена на расстоянии а от оси колеса (будем считать, что a может быть как меньше, так и больше R − такие точки можно найти, например, на железнодорожном колесе). Построим семейство траекторий точек колеса. Пусть в начальный момент времени центр колеса находится в точке О. Введем систему координат, ось X которой проходит вдоль поверхности, по которой катится колесо, а ось Y перпендикулярна этой поверхности и проходит через точку О (рис. 80).

 

рис. 80

 

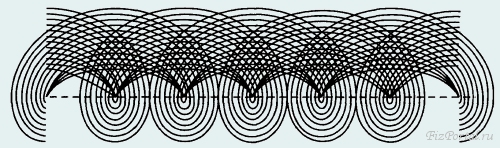
Выберем точку А на расстоянии а от центра и первоначально находящуюся на оси У. Посмотрим, как изменится положение этой точки, когда колесо повернется на некоторый угол φ = ωt (на рисунке это ∠ A^/O^/D). Центр колеса сместится на расстояние S и займет положение О^/, а точка А окажется в точке А^/. Так как движение происходит без проскальзывания, то смещение колеса S = |OO^/| = |BD| будет равно длине дуги DB^/. Поэтому S = Rφ, где угол φ, естественно, измеряется в радианах. Координаты центра колеса будут равны

х _{O '} = S = R φ, у _{O '} = R.

 

Рассматривая треугольник О^/А^/С, легко найти координаты рассматриваемой точки А^/:

 

Посмотрите на эти траектории (рис. 81) при а, изменяющемся от −3R до 3R (с шагом R/4). Не правда ли, эффектные кривые?!

 

 

рис. 81

 

Суперпозиция двух вращательных движений. Посмотрим, какую траекторию описывает точка М колеса радиусом r, катящегося без скольжения по другой неподвижной окружности радиуса R (рис. 82).

 

 

рис. 82

 

Обозначим φ = ωt − угол поворота колеса, m = r/R − отношение радиусов колеса и неподвижной окружности. Пусть А − начальное положение рассматриваемой точки. Из геометрических соображений можно получить параметрическое уравнение траектории точки М:

 

 

Вид траектории полностью определяется параметром m. Если этот параметр является рациональным числом m = p/q, (р, q − целые числа), то траектория является замкнутой.

Посмотрите на различные траектории, описываемые этими  уравнениями (рис. 83). На всех рисунках − в центре изображение окружности, по которой катится колесо.

 

 

рис. 83

¹Дискуссия о том, какое разложение является «правильным», равносильна спору о том, какое разложение «7 = 5 + 2» или «7 = 3 + 4» точнее описывает свойства «семерки».

Суперпозиция и линейность

Возможность «сложения» движений и соответствующих кинематических  характеристик имеет и математическое воплощение. Поясним эту взаимосвязь на простейшем примере (рис. 84).

 

 

рис. 84

 

Пусть материальная точка А движется с угловой скоростью ω^/ = Δα^//Δt по окружности радиуса r с центром, совпадающим с началом координат системы отсчета X^/OY^/, которая, в свою очередь, вращается с угловой скоростью ω_o = Δβ/Δt относительно неподвижной системы отсчета XOY. Угол поворота точки относительно неподвижной системы отсчета, как следует из элементарных геометрических соотношений, равен:

 

α = α^/ + β.

 

Поэтому угловая скорость вращения относительно неподвижной системы отсчета также равна сумме угловых скоростей:

 

ω = Δα/Δt = ω^/ + ω_o.

 

Вычислим теперь, с каким центростремительным ускорением движется точка А. Во вращающейся системе отсчета X^/OY^/ это ускорение равно:

а^/ = r(ω^/)².

 

Ускорение подвижной системы отсчета относительно неподвижной

а_o = r(ω_o)².

 

Ускорение же точки А относительно неподвижной системы отсчета

а = r(ω^/ + ω_o)² ≠ а^/ + а_o.

 

Таким образом, для угловых (и обычных) скоростей принцип суперпозиции выполняется, а для ускорений − нет! Легко заметить, что нарушение принципа суперпозиции для ускорений обусловлено квадратичной зависимостью ускорения от скорости. Скорость же линейно¹ (в данном случае даже пропорционально) выражается через углы поворота. В общем случае, можно утверждать, что математическим выражением принципа суперпозиции для какой-либо физической величины является линейность уравнений, определяющих эту величину.

¹Напомним, что линейная зависимость между величинами у и х выражается уравнением у = kx + b, где k, b − постоянные. Если в этой зависимости b = 0, то говорят, что у и х пропорциональны друг другу.