
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Системы стабилизации, системы программного управления, следящие системы.Стр 1 из 10Следующая ⇒
Передаточные функции звеньев САУ, их связь с дифференциальными уравнениями Отношение оператора воздействия к собственному оператору называютпередаточной функцией или передаточной функцией в операторной форме. Звено, описываемое уравнением (2.26) или, что тоже самое, уравнениями (2.27) — (2.29), можно характеризовать двумя передаточными функциями: передаточной функцией W1(p) по входной величине и, т. е. и передаточной функцией W2(p) по входной величине f, т.е.
Используя передаточные функции, уравнение (2.26) записывают в виде
Уравнения (2.28), (2.29) и (2.32) называют уравнениями в символической или операторной форме записи.
9. Вещественная и мнимая частотные характеристики САУ, их связь с амплитудной и фазовой частотными характеристиками. Проекции вектора W(j w) на действительную и мнимую оси называют соответственно действительной и мнимой частотными характеристиками и обозначают P(w), Q(w). Это позволяет записать АФЧХ в алгебраической форме: W (j w) = P (w) + j Q (w) (2.36) АФЧХ, как и любую комплексную величину, можно также представить в тригонометрической форме W(j w) = A(w)cos j (w) + j A(w)sin j (w). (2.37) Аналитическое выражение для АФЧХ конкретного элемента можно получить из его передаточной функции путем подстановки p = j w: W (j w) = W (p) ½ p = j w. (2.38) Связь между различными частотными характеристиками следующая: A (w) = ç W (j w) ç = j (w) = arg W (j w) =
Типовые звенья САУ Алгоритмические звенья, которые описываются обыкновенными дифференциальными уравнениями первого и второго порядка, получили название типовых динамических звеньев. Типовые динамические звенья являются основными составными частями алгоритмических схем непрерывных САУ, поэтому знание их характеристик существенно облегчает анализ таких систем. Классификацию типовых динамических звеньев удобно осуществить, рассматривая различные частные формы дифференциального уравнения
Инерционное 1-го порядка (апериодическое)
Инерционное 2-го порядка (апериодическое)
T1 ³ 2 T2 Инерционное 2-го порядка (колебательное)
T1 < 2 T2 Идеальное интегрирующее
Идеальное дифференцирующее
Реальное дифференцирующее
Звено запаздывания
Типовые звенья ТАУ 1. К - Усилительное звено. 2. p - Дифференцирующее звено. 3. 1/p - Интегрирующее звено (интегратор). 4. K/(Tp+1) - Инерционное (апериодическое) звено. 5. K/(T2p+2dTp+1) - Колебательное звено. 6. K(Tp+1) - Форсирующее звено. 7. K(T2p+2dTp+1) - Форсирующее звено 2-го порядка.
Критерий: Для устойчивости линейной системы n-го порядка необходимо и достаточно, чтобы годограф Михайлова при изменении частоты в интервале от 0 до ∞, начинаясь в точке на вещественной положительной полуоси последовательно обходил против часовой стрелки n квадрантов комплексной плоскости, не пересекая начало координат. 2-я формулировка: Для устойчивости линейной системы n-го порядка необходимо и достаточно, чтобы при изменении частоты от 0 до ∞ изменение фазы частотной функции характеристического уравнения: Свойства чередования корней. Для устойчивости системы корни должны чередоваться.
Степень затухания
Интенсивность затухания колебаний в системе считается удовлетворительной, если y = 0,75…0,95. Длительность переходного процесса (время регулирования) tп – интервал времени от момента приложения ступенчатого воздействия до момента, после которого отклонения управляемой величины x(t) от ее нового установившегося значения x(¥) становятся меньше некоторого заданного числа d п, т. е. до момента, после которого выполняется условие ê x(t) - x(¥) ê £ d п. В промышленной автоматике величину d п обычно принимают равной 5% от установившегося значения x (¥) [ d п = 0,05 x(¥) ]. Колебательность N – число переходов управляемой величины x(t) через ее установившееся значение x(¥) за время переходного процесса tп.
Основные понятия по Ляпунову об устойчивости нелинейных систем. Основные виды устойчивости нелинейных систем. Устойчивость по Ляпунову: «Невозмущенное движение устойчиво, если при достаточно малых начальных возмущениях вызванное ими возмущенное движение сколь угодно мало отличается от невозмущенного; при этом движение асимптотически устойчиво, если при t Невозмущенным движением системы - одно из возможных расчетных движений системы при некоторых определенных начальных условиях и заданном внешнем воздействии. Всякое другое движение называется возмущенным. Можно считать, что любое возмущенное движение получается за счет приложения к системе кратковременного внешнего возмущения при t = 0. От наличия внешних воздействий на систему, системы управления могут быть разделены на автономные и неавтономные. В автономных системах внешние воздействия отсутствуют. К автономной системе может быть сведена любая из непрерывных систем при не зависящем от времени внешнем воздействии. В неавтономных системах существуют зависящие от времени внешние воздействия. Так как в автономных нелинейных системах наиболее характерными: являются два процесса равновесие и автоколебания, то для них рассматриваются два различных понятия устойчивости: устойчивость равновесия и устойчивость автоколебаний. Для неавтономных систем существует понятие устойчивости процесса, обусловленного внешним воздействием. Состояние равновесия и установившийся режим автоколебаний можно рассматривать как важные частные случаи невозмущенных движений автономной системы. Для общего суждения об устойчивости движения пользуются понятием устойчивости, данным А. М. Ляпуновым: движение устойчиво, если для любой сколь угодно малой заданной области допустимых отклонений k от точки k = 0 можно указать область начальных значений лежащую внутри области и обладающую тем свойством, что ни одно возмущенное движение, начавшееся внутри области никогда не достигнет границы области .
Для характеристики устойчивости кроме областей и удобно ввести понятие области установившихся значений разности возмущенного и невозмущенного движений. При t
Вид области зависит от области начальных отклонений. Нужно отметить два практически важных частных случая областей . В первом случае = 0, т. е.
Такое движение называют асимптотически устойчивым. Если для выполнения равенства (18.4) требуется, чтобы область начальных отклонений была достаточно мала, то говорят об асимптотической устойчивости в малом. Если эта область может иметь конечные размеры, то говорят об асимптотической устойчивости в большом. Если, наконец, равенство (18.4) выполняется при сколь угодно больших начальных отклонениях, то говорят об асимптотической устойчивости в целом. Во втором частном случае область представляет собой отрезок на оси 1. В этом случае равенство (18.4) не выполняется при сколь угодно малых отклонениях от равновесия и устойчивость относится к неасимптотической.
Для суждения об устойчивости автоколебаний вводится понятие орбитальной устойчивости. Периодическое движение (автоколебание) в пространстве состояний изображается некоторой замкнутой кривой Г. Представляя любую траекторию геометрическим местом конца вектора x (t), можно для любого момента времени t определить кратчайшее расстояние ох конца вектора x (t)до кривой Г, которое обозначим [ x (t), Г]. Под орбитально асимптотически устойчивым периодическим движением в автономной системе (автоколебанием) будем понимать такое движение, для которого
Это условие можно выразить с помощью понятия невозмущенного движения, если учесть возможный сдвиг по времени между x H (t) и х (t). Обозначив
можно условие орбитальной асимптотической устойчивости сформулировать следующим образом: существуют такие положительные вещественные значения = 0, для которых
Невыполнение условия (18.5) или (18.7) приводит к нарушению орбитальной асимптотической устойчивости.
Системы стабилизации, системы программного управления, следящие системы. Стабилизирующая САУ – система, алгоритм функционирования которой содержит предписание поддерживать значение управляемой величины постоянным: x (t)» x з = const. (1.3) Знак » означает, что управляемая величина поддерживается на заданном уровне с некоторой ошибкой. Стабилизирующие САУ самые распространенные в промышленной автоматике. Их применяют для стабилизации различных физических величин, характеризующих состояние технологических объектов. Примером стабилизирующей САУ является система регулирования возбуждения синхронного генератора Программная САУ – система, алгоритм функционирования которой содержит предписание изменять управляемую величину в соответствии с заранее заданной функцией времени: x (t)» x з (t) = f п (t). (1.4) Примером программной САУ является система управления активной мощностью нагрузки синхронного генератора на электрической станции в течение суток. Управляемой величиной в системе служит активная мощность нагрузки Р генератора. Закон изменения задания активной мощности Рз (задающего воздействия) определен как функция времени t в течение суток Следящая САУ –система, алгоритм функционирования которой содержит предписание изменять управляемую величину в соответствии с заранее неизвестной функцией времени: x (t)» x з (t) = f с (t). (1.5)
Примером следящей САУ является система управления активной мощностью нагрузки синхронного генератора на электрической станции в течение суток. Управляемой величиной в системе служит активная мощность нагрузки Р генератора. Закон изменения задания активной мощности Рз (задающего воздействия) определяется, например, диспетчером энергосистемы и имеет неопределенный характер в течение суток. В стабилизирующих, программных и следящих САУ цель управления заключается в обеспечении равенства или близости управляемой величины x (t) к ее заданному значению xз (t). Такое управление, осуществляемое с целью поддержания x (t)» x з (t), (1.6) называется регулированием. Управляющее устройство, осуществляющее регулирование, называется регулятором, а сама система – системой регулирования.
5. Преобразование Лапласа. Основные свойства преобразования Лапласа Преобразованием Лапласа называют соотношение
где L – оператор Лапласа. Предполагается, что функция х (t), которая подвергается преобразованию Лапласа, обладает следующими свойствами: х (t) определена и кусочно-дифференцируема на всей положительной числовой полуоси [0, ∞]; х (t) = 0 при t < 0; существуют такие положительные числа М и с, что | x (t) | ≤ Mect при 0 ≤ t < ∞. Функции, обладающие указанными тремя свойствами, часто называют функциями-оригиналами. Соотношение
|
||||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 666; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.29.145 (0.035 с.) |
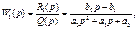 (2.30)
(2.30)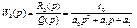 (2.31)
(2.31)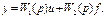 (2.32)
(2.32) Передаточной функцией или передаточной функцией в форме изображений Лапласа называют отношение изображения выходной величины к изображению входной величины при нулевых начальных условиях. Если звено (система) имеет несколько входов, то при определении передаточной функции относительно какой-либо одной входной величины остальные входные величины полагают равными нулю.
Передаточной функцией или передаточной функцией в форме изображений Лапласа называют отношение изображения выходной величины к изображению входной величины при нулевых начальных условиях. Если звено (система) имеет несколько входов, то при определении передаточной функции относительно какой-либо одной входной величины остальные входные величины полагают равными нулю.

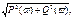 (2.39)
(2.39)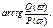 (2.40)
(2.40)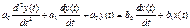 . (3.1) Безинерционное (пропорциональное)
. (3.1) Безинерционное (пропорциональное) 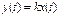 -
- 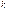
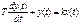 -
- 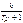
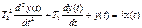 -
- 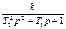
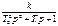
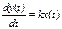 -
- 
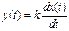 -
- 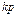
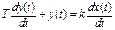 -
- 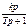
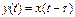 -
- 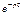
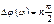
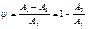 (6.12)
(6.12)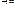 возмущенное движение стремится к невозмущенному.»
возмущенное движение стремится к невозмущенному.»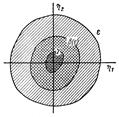 Области и на плоскости 1 и 2 схематически показаны на рис. 18.1
Области и на плоскости 1 и 2 схематически показаны на рис. 18.1
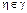 (18.3)
(18.3)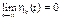 (18.4)
(18.4)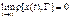 . (18.5)
. (18.5)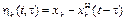 , (18.6)
, (18.6)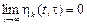 (18.7)
(18.7)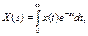 ставящее функции x (t) вещественного переменного в соответствие функцию X (s) комплексного переменного s (s = σ + j ω). При этом х (t) называют оригиналом, а Х(s) — изображением или изображением по Лапласу. То, что х (t) имеет своим изображением Х(s) или оригиналом Х(s) является х (t),записывается так:
ставящее функции x (t) вещественного переменного в соответствие функцию X (s) комплексного переменного s (s = σ + j ω). При этом х (t) называют оригиналом, а Х(s) — изображением или изображением по Лапласу. То, что х (t) имеет своим изображением Х(s) или оригиналом Х(s) является х (t),записывается так: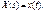 или
или 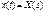 Иногда также пользуются символической записью
Иногда также пользуются символической записью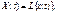
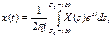 определяющее по известному изображению его оригинал (в точках непрерывности последнего), называют обратным преобразованием Лапласа. В нем интеграл берется вдоль любой прямой ReS = σ0 > с. Символически обратное преобразование Лапласа можно записать так:
определяющее по известному изображению его оригинал (в точках непрерывности последнего), называют обратным преобразованием Лапласа. В нем интеграл берется вдоль любой прямой ReS = σ0 > с. Символически обратное преобразование Лапласа можно записать так: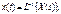 где символ L -1 — обратный оператор Лапласа.
где символ L -1 — обратный оператор Лапласа.


