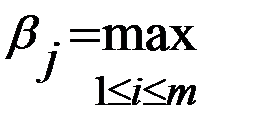Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Платежная матрица. Нижняя и верхняя цена игрыСтр 1 из 7Следующая ⇒
ТЕОРИЯ ИГР
Методические указания для самостоятельной работы студентов по направлению подготовки 38.03.01 – Экономика
Воронеж 2016
УДК 512.8
Раецкая, Е. В. Теория игр [Текст]: методические указания для самостоятельной работы студентов по направлению подготовки 38.03.01 – Экономика / Е. В. Раецкая, И.В. Сапронова, Н.М. Спириной; М-во образования и науки РФ, ФГБОУ ВО «ВГЛТУ». – Воронеж, 2016. – 55 с.
Печатается по решению учебно-методического совета ФГБОУ ВО «ВГЛТУ» (протокол № 5 от 22 апреля 2016 г.)
Рецензент д-р физ.-мат. наук, доцента кафедры математического анализа ВГУ Зубова С.П.
Введение
Целью изучения дисциплины «Теория игр» является воспитание достаточно высокой математической культуры, привитие навыков современных видов математического мышления, ознакомление с математическими моделями конфликтных ситуаций и методами их анализа; применению методов оптимизации, которые могут использоваться при анализе и решении широкого спектра экономических задач. Для достижения поставленной цели, при самостоятельной работе решаются следующие задачи: - самостоятельное усвоение студентом теоретического материала, построенного на основе четких формулировок и доказательстве основных теорем и выработка умения самостоятельно иллюстрировать его примерами и задачами; самостоятельное изучение истории появления наиболее важных понятий и результатов; наряду с изучением основных теоретических результатов при самостоятельной работе с учебными материалами, необходимо обращать внимание на пояснения об их приложениях к другим разделам математики и к решению экономических задач; - закрепление теоретического материала и выработка умения самостоятельно применять математические методы в различных приложениях. В результате самостоятельного освоения дисциплины студент должен: - знать основные понятия, определения и методы исследования объектов с помощью теорем и формул различных разделов курса математики; - уметь: четко формулировать и доказывать основные положения курса математики, решать задачи и примеры по различным разделам высшей математики с доведением решения до практического приемлемого результата (формулы, числа, графика, качественного вывода и т.п.), уметь при решении задач самостоятельно выбирать необходимые вычислительные методы и средства (ПЭВМ, таблицы и справочники); самостоятельно изучать научную литературу по математике;
- иметь представление о численных алгоритмах решения математических и прикладных задач его профессиональной области. Студент по результатам освоения дисциплины «Теория игр» должен обладать способностью выбрать инструментальные средства для обработки экономических данных в соответствии с поставленной задачей, проанализировать результаты расчетов и обосновать полученные выводы.
Содержание Введение……………………………………………………………………………..3 1.Матричные игры ………………………………………………………………...4 1.1 Платежная матрица. Нижняя и верхняя цена игры……………………...4 1.2. Игры с седловой точкой………………………………………………………7 1.3. Игры, повторяемые многократно. Смешанные стратегии……………....9 1.4. Аналитический метод решения игры размера 2 2.Биматричные игры …………………………………………………………….16 2.1. Бескоалиционные биматричные игры в нормальной форме …...….…..16 2.2. Анализ доминирования платежных матриц ……………………………...20 2.3. Р авновесие по Нэшу в чистых стратегиях………………………………...21 2.4. Р авновесие по Нэшу в смешанных стратегиях…………………………..24 2.5. Аналитический метод решения биматричной игры 2 2.6. Графический метод решения биматричной игры 2 3. Игры с природой…… ………………………………………………………….42 3.1 Принятие решений в условиях неопределенности…………...………....42 3. 2. Принятие решений в условиях риска………………………………...…...48 3.3. Производные критерии в играх с природой………………………...…....50 Вопросы для контроля. ………………………………………………………….54 Библиографический список…………………………………………………….55 МАТРИЧНЫЕ ИГРЫ Игры с седловой точкой Для игры с седловой точкой рассмотрим такой элемент платежной матрицы
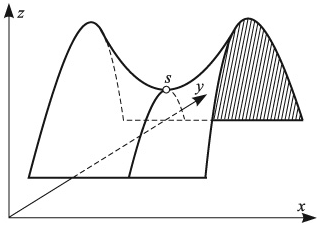
Следовательно, выполняется равенство Элемент платежной матрицы Как известно, в геометрии точку на поверхности, являющуюся одновременно минимумом по одной оси координат и максимумом по другой, называют седловой точкой (см. рис. 2.1).
Рис. 1.1. Поверхность с седловой точкой По аналогии с геометрией элемент Минимаксные стратегии В случае игры с седловой точкой минимаксные стратегии обладают своеобразной «устойчивостью»: если одна сторона придерживается своей оптимальной стратегии, то для другой может быть только невыгодным отклоняться от своей. Заметим, что тогда наличие у любого игрока сведений о том, что противник избрал свою оптимальную стратегию, не может изменить собственного поведения игрока. Если он не хочет действовать против своих же интересов, то он должен придерживаться своей оптимальной стратегии. Пара оптимальных стратегий в игре с седловой точкой является как бы «положением равновесия». Любое отклонение от оптимальной стратегии приводит отклоняющегося игрока к невыгодным последствиям, вынуждающим его вернуться в исходное положение. Класс игр, имеющих седлову точку, представляет интерес, как с теоретической, так и с практической точки зрения. В теории игр доказывается, что, в частности, каждая игра с полной информацией имеет седловую точку, и, следовательно, каждая такая игра имеет решение, т.е. существует пара оптимальных стратегий той и другой стороны, дающая средний выигрыш, равный цене игры. Если игра с полной информацией состоит только из личных ходов, то при применении каждой стороной своей оптимальной стратегии она должна всегда кончаться вполне определенным исходом, а именно, выигрышем в точности равным цене игры. В качестве примера игры с полной информацией приведем известную игру с укладыванием монет на круглый стол. Два игрока поочередно кладут одинаковые монеты на круглый стол, выбирая каждый раз произвольное положение центра монеты (взаимное накрывание монет не допускается). Выигрывает тот из игроков, кто положил последнюю монету (когда места для других монет уже не останется). Очевидно, что исход этой игры всегда предрешен, и существует вполне определенная стратегия, обеспечивающая достоверный выигрыш тому из игроков, кто кладет монету первым. А именно, он должен первый раз положить монету в центр стола, а далее на каждый ход противника отвечать симметричным ходом. При этом второй игрок может вести себя как угодно, не изменяя предрешенного результата игры. Поэтому данная игра имеет смысл только для игроков, не знающих оптимальной стратегии. Аналогично дело обстоит с шахматами и с другими играми с полной информацией. Любая из таких игр обладает седловой точкой и решением, указывающим каждому из игроков его оптимальную стратегию. Решение шахматной игры не найдено только потому, что число комбинаций возможных ходов в шахматах слишком велико, чтобы можно было построить платежую матрицу и найти в ней седловую точку.
З а м е ч а н и е. Могут встречаться случаи, когда платежная матрица имеет несколько седловых точек, однако это не изменит характера рекомендуемых решений, поскольку все ситуации равновесия имеют одну и ту же цену и, следовательно, эквиваленты. Однако наличие седловой точки в игре это далеко не правило, а скорее исключение, так как большинство матричных игр не имеет седловой точки. Возникает вопрос, как найти решение игры, платежная матрица которой не имеет седловой точки? БИМАТРИЧНЫЕ ИГРЫ 2.1 Бескоалиционные биматричные игры в нормальной форме Рассматривается конечная бескоалиционная игра двух лиц с ненулевой суммой, которая называется биматричной игрой. Это неантагонистическая игра, формализующая конфликтную ситуацию, в которой интересы сторон (игроков) не являются противоположными. В играх такого рода при одинаковых совокупностях стратегий игроки получают различные выигрыши. Игра может быть представлена двумя матрицами одинаковых размерностей. Это матрица А (таблица 2.1) и матрица В (таблица 2.2) выигрышей, соответственно, первого и второго игроков.
Т а б л и ц а 2.1 Матрица А - матрица выигрышей первого игрока
Строки этих матриц ставятся во взаимно однозначное соответствие стратегиям Каждый элемент первой матрицы
В биматричных играх, в отличие от игр с нулевой сумой, конфликт интересов участников игры может быть не таким острым, как в матричных, Т а б л и ц а 2.2 Матрица В - матрица выигрышей второго игрока
поскольку здесь выигрыш одного из игроков сопровождается в общем случае не равным по величине проигрышем другого игрока.
Снижение остроты конфликта, а так же участие в игре достаточно большого числа игроков создают благоприятные условия для создания коалиций и коопераций, то есть согласованного взаимодействия отдельных участников игры. Однако в данном разделе рассматриваются бескоалиционныебиматричные игры в нормальной форме. Рассмотрим примеры биматричных игр. Одной из наиболее известных является так называемая «Дилемма заключенных», для которой существует несколько различных вариантов. П р и м е р 2.1. «Дилемма заключенных» "Игроками" являются двое заключенных, обвиняемых в совершении тяжелого преступления. Каждый из них располагает двумя стратегиями: сознаваться ( В игре возможны следующие ситуации: – оба сознаются (набор стратегий – оба не сознаются ( – если первый сознается, а второй нет ( – если сознается второй, а первый нет ( Здесь В качестве значений платежных матриц берутся сроки заключения с обратными знаками. Игра задается платежными матрицами первого и второго игроков:
Пример 1. Равновесие с доминирующей стратегий одного из игроков Т а б л и ц а 2.5 Т а б л и ц а 2.6
Матрица А Матрица В
Первая стратегия первого игрока является доминирующей, о чем свидетельствует появление двух выделенных элементов в первой строке его платежной матрицы. У второго игрока доминирующая стратегия отсутствует. Однако, в данном случае пара чистых стратегий Замечание. Равновесие Нэша – это некооперативное равновесие, которое, по сути, представляет конкурентное равновесие, являющееся результатом принятия решений игроками, не вступающими ни в какие соглашения друг с другом и имеющими цель максимизации собственного выигрыша.
Другими словами, каждый игрок заботится о минимизации последствий непредсказуемых действий конкурента.
Замечание. Равновесие Нэша в биматричных играх представляет собой обобщение понятия седловой точки (оптимальное решение) в играх с нулевой суммой. ИГРЫ С ПРИРОДОЙ Критерий Гермейера. Этот критерий обычно применяют при решении задач, в которых речь идет о затратах, то есть анализируется матрица выигрышей, значения в которой взяты с обратными знаками ЛПР принимает гипотезу: число (ЛПР относится к выбору В качестве оценки стратегии Замечание. В случае, когда все состояния природы Замечание. В некоторых случаях, применяя критерий Гермейера, ЛПР достаточно серьезно рискует. Это касается тех ситуаций, в которых нет надежной информации о функции распределения, а также в случае малых чисел реализации.
Критерий произведений. ЛПР анализирует матрицу выигрышей и, если она содержит отрицательные элементы, вводит в рассмотрение константу Тогда далее рассматривается матрица Применение этого критерия обусловлено тем, что вероятности появления состояния В качестве оценки стратегии Оптимальная по данному критерию стратегия Замечание. Поскольку различные критерии связаны с различными условиями, в которых принимается решение, лучшее всего для сравнительной оценки рекомендации тех или иных критериев получить дополнительную информацию о самой ситуации. Как правило, критерии применимы только для идеализированных практических решений, вследствие их жёстких исходных позиций. Практикуется применение поочерёдно различных критериев. После этого среди нескольких вариантов ЛПР волевым методом выбирает окончательное решение. Такой подход позволяет, во-первых, лучше проникнуть во все внутренние связи проблемы принятия решений и, во-вторых, ослабляет влияние субъективного фактора.
Вопросы для контроля 1. Дайте определение платежной матрицы игры. 2. Сформулируйте определения нижней и верхней цены игры. 3. Опишите суть принципа минимакса. 4. Дайте определение игры с седловой точкой. 5. Сформулируйте определение седловой точки. 6. Дайте определение цены игры. 7. Дайте определения чистых и смешанных стратегий игроков. 8. Сформулируйте основную теорему теории игр. 9. Сформулируйте теорему об активных стратегиях. 10. Опишите аналитический метод решения игры 2 11. Опишите графический метод решения игры 2 12. Опишите графический метод решения игры m 16. Опишите общую схему решения парных игр с нулевой суммой. 17. Поясните, в каком случае возникает биматричная игра, чем она задается? 18. Как можно задать функции выигрыша игроков? 19. Как определяется ситуация равновесия в биматричной игре? 20. В чем содержательный смысл ситуации равновесия? 21. Поясните, в каком смысле седловая точка является частным случаем ситуации равновесия? 22. Всегда ли в биматричной игре есть ситуация равновесия? 23. Что понимается под возможной в игре неустойчивостью ситуации равновесия? 24. Всегда ли в биматричной игре есть чистая ситуация равновесия? 25. Опишите алгоритм поиска ситуации равновесия в биматричных играх размерности 2×2. 26. Как определяются смешанные стратегии игроков и функции выигрыша игроков в смешанных стратегиях? 27. Какая пара стратегий игроков называется оптимальной по Парето? 28. Что означает оптимальность по Парето? 29. Оъясните, что подразумевается под термином "природа" в теории игр. 30.Поясните постановку задачи принятия решения в условиях неопределенности. 31. Приведите примеры факторов, определяющих состояния системы. 32. Сформулируйте постановку задачи принятия решения в условиях неопределенности. 33. Объясните, как задается функция выигрыша в задачах принятия решения в условиях неопределенности. 34. Поясните, в чем заключается основная цель задачи принятия решения в условиях неопределенности. 35. Объясните, что понимается под оптимальными стратегиями игроков. 36. Приведите способы сравнения двух стратегий. 37. Сформулируйте принцип доминирования. 38. Перечислите основные методы, позволяющие найти оптимальную стратегию в ЗПР в условиях неопределенности. 39. Разъясните, в чем заключается суть анализа доминирования стратегий. 40. Сформулируйте основные критерии принятия решений в условиях неопределенности. 41. Объясните, на каких гипотезах основаны критерии принятия решений в условиях неопределенности. 42. Поясните, как задается вероятностная мера на множестве состояний природы, если множество конечно. 43. Сформулируйте постановку задачи принятия решения в условиях риска. 44. Сформулируйте основные критерии принятия решений в условиях риска. 45. Поясните, каким параметром численно оценивается степень доверия игрока к априори заданным вероятностям наступления различных состояний природы. 46.Сформулируйте производные критерии в играх с природой.
Библиографический список Основная литература: 1. Конюховский, В.П. Теория игр: учебник для бакалавров / П.В. Конюховский, А.С. Малова. - М.: Издательство Юрайт, 2013. - 252 с. - Серия: Бакалавр. Базовый курс. – ЭБС «Юрайт»
Дополнительная литература:
1. Сапронов И. В. Теория игр [Текст]: учеб. пособие: для студентов по направлению подгот. 080100 – Экономика / И. В. Сапронов, Е. О. Уточкина. Е. В. Раецкая; ВГЛТА. - Воронеж, 2013. - 204 с. - Электронная версия в ЭБС ВГЛТА. ТЕОРИЯ ИГР
Методические указания для самостоятельной работы студентов по направлению подготовки 38.03.01 – Экономика
Воронеж 2016
УДК 512.8
Раецкая, Е. В. Теория игр [Текст]: методические указания для самостоятельной работы студентов по направлению подготовки 38.03.01 – Экономика / Е. В. Раецкая, И.В. Сапронова, Н.М. Спириной; М-во образования и науки РФ, ФГБОУ ВО «ВГЛТУ». – Воронеж, 2016. – 55 с.
Печатается по решению учебно-методического совета ФГБОУ ВО «ВГЛТУ» (протокол № 5 от 22 апреля 2016 г.)
Рецензент д-р физ.-мат. наук, доцента кафедры математического анализа ВГУ Зубова С.П.
Введение
Целью изучения дисциплины «Теория игр» является воспитание достаточно высокой математической культуры, привитие навыков современных видов математического мышления, ознакомление с математическими моделями конфликтных ситуаций и методами их анализа; применению методов оптимизации, которые могут использоваться при анализе и решении широкого спектра экономических задач. Для достижения поставленной цели, при самостоятельной работе решаются следующие задачи: - самостоятельное усвоение студентом теоретического материала, построенного на основе четких формулировок и доказательстве основных теорем и выработка умения самостоятельно иллюстрировать его примерами и задачами; самостоятельное изучение истории появления наиболее важных понятий и результатов; наряду с изучением основных теоретических результатов при самостоятельной работе с учебными материалами, необходимо обращать внимание на пояснения об их приложениях к другим разделам математики и к решению экономических задач; - закрепление теоретического материала и выработка умения самостоятельно применять математические методы в различных приложениях. В результате самостоятельного освоения дисциплины студент должен: - знать основные понятия, определения и методы исследования объектов с помощью теорем и формул различных разделов курса математики; - уметь: четко формулировать и доказывать основные положения курса математики, решать задачи и примеры по различным разделам высшей математики с доведением решения до практического приемлемого результата (формулы, числа, графика, качественного вывода и т.п.), уметь при решении задач самостоятельно выбирать необходимые вычислительные методы и средства (ПЭВМ, таблицы и справочники); самостоятельно изучать научную литературу по математике; - иметь представление о численных алгоритмах решения математических и прикладных задач его профессиональной области. Студент по результатам освоения дисциплины «Теория игр» должен обладать способностью выбрать инструментальные средства для обработки экономических данных в соответствии с поставленной задачей, проанализировать результаты расчетов и обосновать полученные выводы.
Содержание Введение……………………………………………………………………………..3 1.Матричные игры ………………………………………………………………...4 1.1 Платежная матрица. Нижняя и верхняя цена игры……………………...4 1.2. Игры с седловой точкой………………………………………………………7 1.3. Игры, повторяемые многократно. Смешанные стратегии……………....9 1.4. Аналитический метод решения игры размера 2 2.Биматричные игры …………………………………………………………….16 2.1. Бескоалиционные биматричные игры в нормальной форме …...….…..16 2.2. Анализ доминирования платежных матриц ……………………………...20 2.3. Р авновесие по Нэшу в чистых стратегиях………………………………...21 2.4. Р авновесие по Нэшу в смешанных стратегиях…………………………..24 2.5. Аналитический метод решения биматричной игры 2 2.6. Графический метод решения биматричной игры 2 3. Игры с природой…… ………………………………………………………….42 3.1 Принятие решений в условиях неопределенности…………...………....42 3. 2. Принятие решений в условиях риска………………………………...…...48 3.3. Производные критерии в играх с природой………………………...…....50 Вопросы для контроля. ………………………………………………………….54 Библиографический список…………………………………………………….55 МАТРИЧНЫЕ ИГРЫ Платежная матрица. Нижняя и верхняя цена игры
Рассмотрим парную конечную игру с нулевой суммой. Пусть игрок А располагает m личными стратегиями В результате выбора игроками любой пары стратегий Матрица Поставим задачу: определить оптимальные стратегии игроков. Выбирая стратегию Обозначим через Число Стратегия, соответствующая максимину, называется максиминной стратегией. Таким образом, если игрок А будет придерживаться максиминной стратегии, то ему гарантирован выигрыш, не меньше, чем Проанализируем теперь платежную матрицу с точки зрения игрока В, заинтересованного в том, чтобы игрок А выиграл, как можно меньше. Если игрок В выберет стратегию Следовательно, игроку В нужно выбрат
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 174; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.187.106 (0.161 с.) |
 2………………….11 1.5. Графический метод решения игр 2
2………………….11 1.5. Графический метод решения игр 2 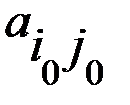 , который соответствует минимаксным стратегиям
, который соответствует минимаксным стратегиям 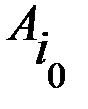 и
и 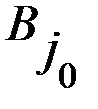 . Этот элемент является одновременно минимальным в своей строке и максимальным в своем столбце, и выполняются равенства
. Этот элемент является одновременно минимальным в своей строке и максимальным в своем столбце, и выполняются равенства =
= 
 =
= 
 .
.
 .
.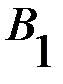

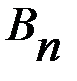


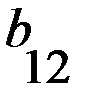
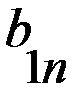
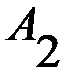

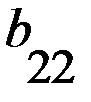
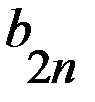

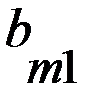
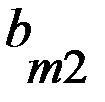
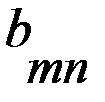
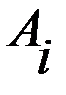 первого игрока, а столбцы
первого игрока, а столбцы 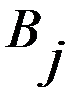 стратегиям второго игрока.
стратегиям второго игрока. 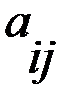 представляет численное значение выигрышей первого игрока при стратегиях
представляет численное значение выигрышей первого игрока при стратегиях  , а каждый элемент второй матрицы
, а каждый элемент второй матрицы 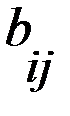 представляет численное значение выигрышей второго игрока в аналогичных ситуациях.
представляет численное значение выигрышей второго игрока в аналогичных ситуациях.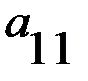
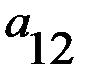


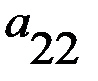
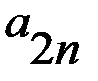
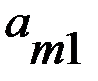
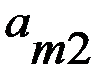
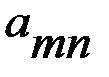
 лет заключения (большой срок, но не максимальный);
лет заключения (большой срок, но не максимальный);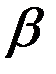 лет за менее тяжкие преступления, в которых они уже уличены;
лет за менее тяжкие преступления, в которых они уже уличены;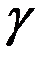 лет, а второй получает максимальный срок в
лет, а второй получает максимальный срок в  лет;
лет;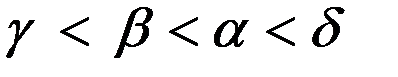 .
. ,
, 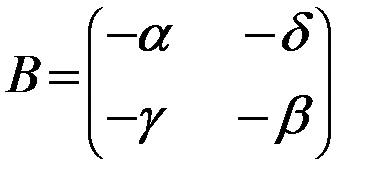 .
.



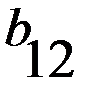
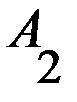

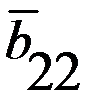
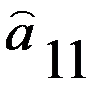
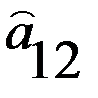
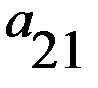
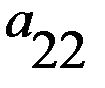
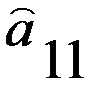
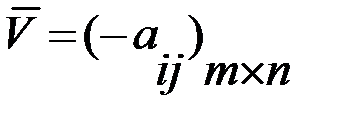 . Если среди значений «
. Если среди значений «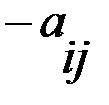 » встречаются положительные, то, подобрав подходящим образом некое число
» встречаются положительные, то, подобрав подходящим образом некое число 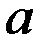 (
(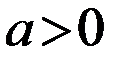 ), переходят к строго отрицательным значениям с помощью преобразования (
), переходят к строго отрицательным значениям с помощью преобразования (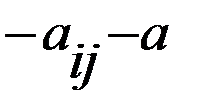 ), при подходящем образом подобранном a > 0.
), при подходящем образом подобранном a > 0.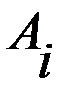 берется величина
берется величина  . Оптимальная по данному критерию стратегия
. Оптимальная по данному критерию стратегия 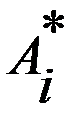 находится из условия
находится из условия  .
.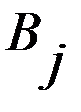 – равновероятны (наступают с вероятностями
– равновероятны (наступают с вероятностями 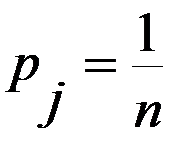 ), критерий Гермейера обобщает ММ-критерий.
), критерий Гермейера обобщает ММ-критерий. , так что все значения матрицы выигрышей «сдвигаются» на величину указанной константы.
, так что все значения матрицы выигрышей «сдвигаются» на величину указанной константы.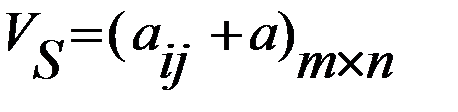 . Чаще всего принимают
. Чаще всего принимают  .
. .
. .
. , …,
, …,  , …,
, …, 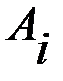 и
и 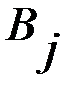 (i = 1, 2, 3, …, m; j = 1, 2, 3, …, n) однозначно определяется исход игры, т.е. выигрыш
(i = 1, 2, 3, …, m; j = 1, 2, 3, …, n) однозначно определяется исход игры, т.е. выигрыш 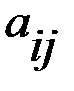 игрока А (положительный или отрицательный) и проигрыш (–
игрока А (положительный или отрицательный) и проигрыш (– 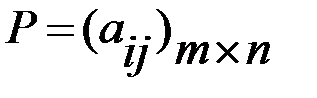 (i = 1, 2, 3, …, m; j = 1, 2, 3, …, n), элементами которой являются выигрыши, соответствующие стратегиям
(i = 1, 2, 3, …, m; j = 1, 2, 3, …, n), элементами которой являются выигрыши, соответствующие стратегиям 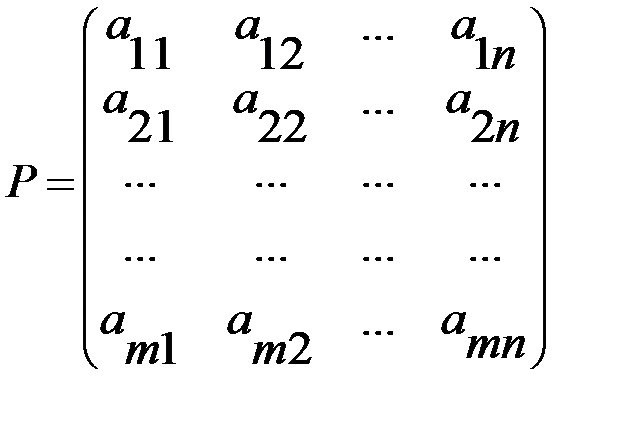 .
. наименьший выигрыш игрока А при выборе им стратегии
наименьший выигрыш игрока А при выборе им стратегии 
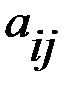 . Следовательно, для получения наибольшего выигрыша игроку А нужно выбирать ту из стратегий, для которой число
. Следовательно, для получения наибольшего выигрыша игроку А нужно выбирать ту из стратегий, для которой число 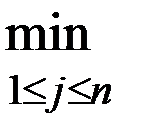
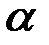 , при любом поведении игрока В.
, при любом поведении игрока В.