
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Закон нормального (гауссовского) распределения. ⇐ ПредыдущаяСтр 5 из 5
Закон распределения вероятностей непрерывной случайной величины X называется нормальным, если её плотность вероятности определяется формулой:
где График функции f(x) (кривая Гаусса) имеет следующий вид (точка максимума
Нормальное распределение с параметрами
Для этой функции составлена таблица её значений для положительных значений x (функция
Эту кривую называют единичной нормальной кривой. Она играет роль стандарта, т.е. любые собранные в статистических исследованиях данные стремятся преобразовать так, чтобы кривая их распределения была максимально близка к этой стандартной кривой. Пусть случайная величина X распределена по нормальному закону. Тогда вероятность того, что X примет значение, принадлежащее интервалу
Сделаем замену
Интеграл
которая называется функцией Лапласа или интегралом вероятностей. Для функции Лапласа составлена таблица её значений для положительных значений x. Свойства функции Лапласа. 1. Доказательство: 2. Ф(x) – нечётная функция, т.е. Ф(- x)=-Ф(x). Доказательство:
3. Функция Ф( x) монотонно возрастает. Из формул (2) и (3) следует, что вероятность того, что случайная величина X примет значение из интервала
Пример. Случайная величина X распределена по нормальному закону. Математическое ожидание и среднее квадратическое отклонение этой величины соответственно равны 0 и 2. Найти вероятность того, что X примет значение, принадлежащее интервалу (-2;3).
Часто требуется вычислить вероятность того, что отклонение нормально распределённой случайной величины X от её математического ожидания по абсолютной величине меньше заданного положительного числа
Таким образом,
Пример. Пусть случайная величина X распределена по нормальному закону с параметрами
Нормальное распределение вероятностей имеет в теории вероятностей большое значение. В частности, закон распределения суммы достаточно большого числа независимых случайных величин, влияние каждой из которых на всю сумму ничтожно мало, близок к нормальному распределению. Этот факт получил название центральной предельной теоремы.
|
|||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 43; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.27.91 (0.006 с.) |
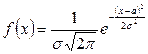 , (1)
, (1)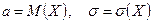 .
. ), причём его максимальная ордината
), причём его максимальная ордината  убывает с возрастанием значения
убывает с возрастанием значения  (кривая «сжимается» к оси OX) и возрастает с убыванием значения
(кривая «сжимается» к оси OX) и возрастает с убыванием значения 

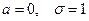 называется нормированным. Функция плотности вероятности для такого распределения имеет вид:
называется нормированным. Функция плотности вероятности для такого распределения имеет вид: .
.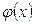 чётная). График
чётная). График 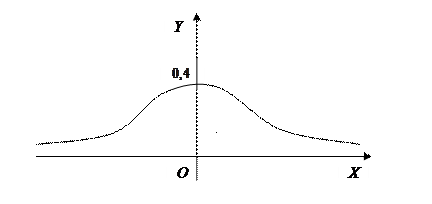
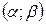 равна:
равна: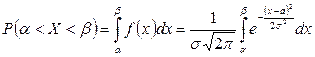 .
.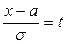 , тогда
, тогда 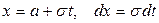 , получаем:
, получаем: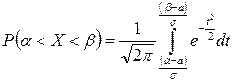 . (2)
. (2)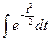 не вычисляется в элементарных функциях, поэтому для вычисления интеграла (2) вводится функция
не вычисляется в элементарных функциях, поэтому для вычисления интеграла (2) вводится функция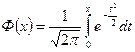 , (3)
, (3)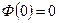 .
.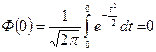 .
.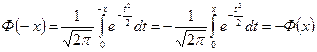 (замена t=- z, dt=- dz).
(замена t=- z, dt=- dz). равна:
равна: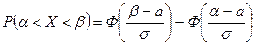 . (4)
. (4)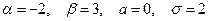 . По формуле (4) получаем:
. По формуле (4) получаем: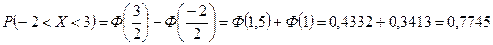 .
.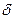 , т.е. найти
, т.е. найти 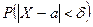 . По формуле (4) получаем:
. По формуле (4) получаем: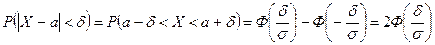 .
.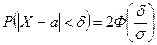 . (5)
. (5)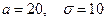 . Найти
. Найти 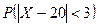 .
.



