
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Математическое ожидание и дисперсия непрерывной случайной величины
Определение 1. Математическим ожиданием непрерывной случайной величины X с плотностью вероятности f(x) называется величина несобственного интеграла (если он сходится):
Определение 2. Дисперсией непрерывной случайной величины X, математическое ожидание которой M(X)= a, а функция f(x) является её плотностью вероятности, называется величина несобственного интеграла (если он сходится):
Математическое ожидание и дисперсия непрерывной случайной величины имеют те же свойства, что и математическое ожидание и дисперсия дискретной случайной величины. Для непрерывной случайной величины среднее квадратическое отклонение определяется, как и для дискретной величины: Пример. Случайная величина X задана плотностью вероятности:
Определить математическое ожидание, дисперсию и среднее квадратическое отклонение величины X.
ЛЕКЦИЯ 4: «ЗАКОНЫ РАСПРЕДЕЛЕНИЯ СЛУЧАЙНЫХ ВЕЛИЧИН» Равномерное распределение Распределение вероятностей непрерывной случайной величины X, принимающей все значения из отрезка [ a; b], называется равномерным, если её плотность вероятности на этом отрезке постоянна, а вне его равна нулю, т.е.
Так как
Определим математическое ожидание, дисперсию и среднее квадратическое отклонение для случайной величины с равномерным распределением.
Таким образом,
Таким образом, Пример. Все значения равномерно распределённой случайной величины лежат на отрезке [2;8]. Найти вероятность попадания случайной величины в промежуток (3;5). a=2, b=8, Биномиальное распределение Пусть производится n испытаний, причём вероятность появления события A в каждом испытании равна p и не зависит от исхода других испытаний (независимые испытания). Так как вероятность наступления события A в одном испытании равна p, то вероятность его ненаступления равна q=1- p. Пусть событие A наступило в n испытаниях m раз. Это сложное событие можно записать в виде произведения:
Тогда вероятность того, что при n испытаниях событие A наступит m раз
или
Формула (1) называется формулой Бернулли. Пример. Пусть всхожесть семян данного растения составляет 90%. Найти вероятность того, что из четырёх посеянных семян взойдут: 1) три; 2) не менее трёх. 1) m=3, n=4, p=0,9, q=1-0,9=0,1,
2) P (A) =0,2916+0,6561=0,9477. Пусть X – случайная величина, равная числу появлений события A в n испытаниях, которая принимает значения
Полученный закон распределения случайной величины называется законом биномиального распределения.
Математическое ожидание, дисперсия и среднее квадратическое отклонение случайных величин, распределённых по биномиальному закону, определяются по формулам:
Пример. По мишени производятся три выстрела, причём вероятность попадания при каждом выстреле равна 0,8. Рассматривается случайная величина X – число попаданий в мишень. Найти её закон распределения, математическое ожидание, дисперсию и среднее квадратическое отклонение. p=0,8, q=0,2, n=3,
Получаем закон распределения:
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 81; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.246.203 (0.006 с.) |
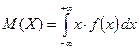 .
.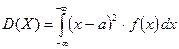 .
.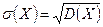 .
.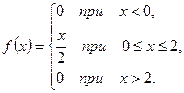
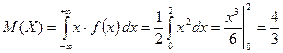 ;
;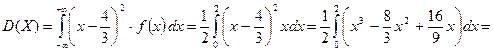
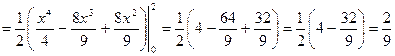 ;
;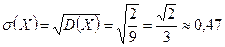 .
.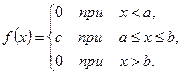
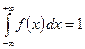 , получаем
, получаем 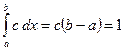 , отсюда
, отсюда 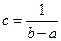 .
. Таким образом, плотность вероятности непрерывной случайной величины X, распределённой равномерно на отрезке [ a; b], имеет вид:
Таким образом, плотность вероятности непрерывной случайной величины X, распределённой равномерно на отрезке [ a; b], имеет вид: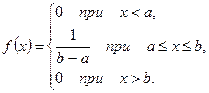
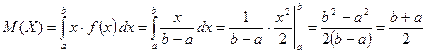 .
.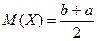 , как и должно, быть в силу симметрии распределения.
, как и должно, быть в силу симметрии распределения.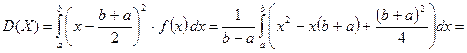
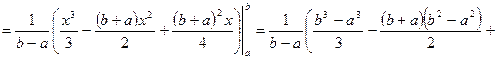

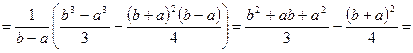
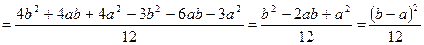 .
.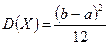 , тогда
, тогда 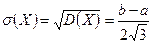 .
.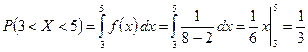 .
.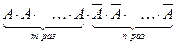 .
.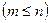 , вычисляется по формуле:
, вычисляется по формуле: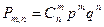
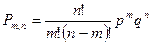 (1)
(1)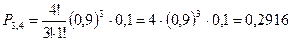 ;
;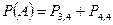 ,
, 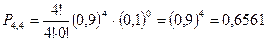 ;
;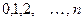 с вероятностями:
с вероятностями: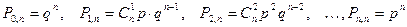 .
.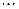
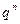
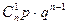
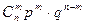
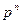
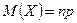 ,
, 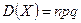 ,
, 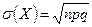 .
.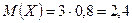 ,
, 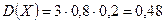 ,
, 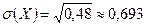 .
.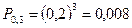 - вероятность 0 попаданий;
- вероятность 0 попаданий;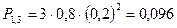 - вероятность одного попадания;
- вероятность одного попадания;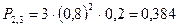 - вероятность двух попаданий;
- вероятность двух попаданий;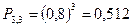 - вероятность трёх попаданий.
- вероятность трёх попаданий.


