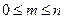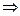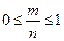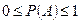Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Классическое определение вероятности. Лекция 1: «основные понятия теории вероятностей»Стр 1 из 5Следующая ⇒
ЛЕКЦИЯ 1: «ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ» Понятие о случайном событии Опыт, эксперимент, наблюдение явления называется испытанием. Примеры: бросание монеты, бросание игральной кости. Результат, исход испытания называется событием. Примеры: выпадение герба, появление того или иного числа очков на брошенной игральной кости. Для обозначения событий используют большие буквы латинского алфавита: A, B, C и т.д. Определение 1. Два события называются совместимыми, если появление одного из них не исключает появление другого в одном и том же испытании. Пример. Испытание – однократное бросание игральной кости. Событие A – появление четырёх очков, событие B - появление чётного числа очков. Определение 2. Два события называют несовместимыми, если появление одного из них исключает появление другого в одном и том же испытании. Пример. Испытание – однократное бросание монеты. Событие A – выпадение герба, событие B - выпадение цифры. Определение 3. Два события A и B называются противоположными, если в данном испытании они несовместимы и одно из них обязательно происходит. Событие, противоположное событию A, обозначают через Определение 4. Событие называют достоверным, если в данном испытании оно является единственно возможным его исходом, и невозможным, если в данном испытании оно заведомо не может произойти. Определение 5. Событие называют случайным, если оно объективно может наступить или не наступить в данном испытании. Пример. Событие A – выпадение шести очков при бросании игральной кости – случайное. Можно ли как-то измерить возможность появления некоторого случайного события? Задачи 1. В ящике 15 белых, 12 красных и 14 синих шаров. Вынули один шар. Определить вероятность того, что вынутый шар красный. 2. В денежно-вещевой лотерее на серию из 1000 билетов приходится 3 денежных и 8 вещевых выигрышей. Какова вероятность какого-либо выигрыша на один лотерейный билет? 3. Бросается один раз игральная кость. Какова вероятность того, что выпадет 1 или 5 очков? 4. В ящике 8 белых и 4 синих шара. Вынули сразу 2 шара. Определить вероятность того, что все шары синие? 5. В коробке 20 ламп - 18 исправных и 2 бракованных. Из коробки вынимают 3 лампы. Какова вероятность того, что все они исправные?
6. Бросается один раз игральная кость. Какова вероятность того, что выпадет 1 или 5 очков? 7. Сколько различных слов можно получить перестановками всех букв в слове ЖУК? 8. Сколько различных слов можно получить перестановками всех букв в слове МАТЕМАТИКА? 9. Сколькими способами из 5 шаров можно выбрать 2? 10. Сколькими способами из 10 студентов можно выбрать 3 делегатов на конференцию? Свойства вероятности Формула полной вероятности Теорема. Вероятность события A, которое может наступить лишь при условии появления одного из n попарно несовместимых событий
Формула (3) называется формулой полной вероятности. Доказательство: самостоятельно Примеры. 1) Имеются три одинаковых по виду ящика. В первом находятся две белые мыши и одна серая, во втором – три белые и одна серая, в третьем – две белые мыши и две серые мыши. Какова вероятность того, что из наугад выбранного ящика будет извлечена белая мышь? Событие событие событие событие A - извлечение белой мыши. Так как все ящики одинаковы, то
По формуле (3) получаем:
2) Для приёма зачёта преподаватель заготовил 50 задач: 20 задач по дифференциальному исчислению, 30 задач по интегральному исчислению. Для сдачи зачёта студент должен решить первую же доставшуюся ему наугад задачу. Какова вероятность для студента сдать зачёт, если он умеет решать 18 задач по дифференциальному исчислению и 15 задач по интегральному исчислению. Событие событие событие A – задача решена. Тогда
Применяем формулу (3):
Задачи 1. Участники жеребьевки достают из ящика жетоны с номерами от 1 до 100. Найти вероятность того, что номер первого наудачу извлечённого жетона не содержит цифры 5. 2. В ящике 7 белых и 12 чёрных шаров. Вынули два шара. Определить вероятность того, что оба шара чёрные.
3. В группе из 30 студентов на контрольной работе получили: 6 студентов – оценку «5», 10 студентов – оценку «4», 9 студентов – оценку «3». Какова вероятность того, что все 3 студента, вызванные к доске, получили оценку «2» по контрольной работе? 4. В ящике 10 белых, 15 чёрных, 20 синих и 25 красных шаров. Вынули один шар. Какова вероятность того, что вынутый шар белый? чёрный? синий? красный? белый или чёрный? синий или красный? белый, чёрный или синий? 5. В первом ящике 2 белых и 10 чёрных шаров. Во втором ящике 8 белых и 4 чёрных шара. Из каждого ящика вынули по одному шару. Какова вероятность того, что оба шара белые? 6. В первом ящике 6 шаров: 1 белый, 2 красных и 3 синих. Во втором ящике 12 шаров: 2 белых, 6 красных и 4 синих. Из каждого ящика вынули по одному шару. Какова вероятность того, что среди вынутых шаров нет синих? 7. В ящике 6 белых и 8 чёрных шаров. Из ящика вынули 2 шара (не возвращая вынутый шар в ящик). Какова вероятность того, что оба шара белые?
Свойства дисперсии. 1. 2. 3. 4. Определение 3. Средним квадратическим отклонением
Пример. Случайная величина X – число очков, выпавших при однократном бросании игральной кости. Определить Закон распределения случайной величины X задан таблицей:
Находим математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины X:
Введение среднего квадратического отклонения объясняется тем, что дисперсия измеряется в квадратных единицах относительно размерности самой случайной величины. В тех случаях, когда нужно иметь числовую характеристику рассеяния возможных значений в той же размерности, что и сама случайная величина, используется среднее квадратическое отклонение. Задачи 1. Имеется четыре ящика. В первом ящике 2 белых и 2 чёрных шара, во втором – 3 белых и 4 чёрных шара, в третьем – 3 белых и 8 чёрных шаров, в четвёртом – 6 белых и 7 чёрных шаров. Выбирают наугад один из ящиков и вынимают из него шар. Найти вероятность того, что этот шар белый. 2. Имеется четыре ящика. В первом ящике 3 белых и 3 чёрных шара, во втором – 2 белых и 4 чёрных шара, в третьем – 2 белых и 8 чёрных шаров, в четвёртом – 6 белых и 7 чёрных шаров. Выбирают наугад один из ящиков и вынимают из него шар. Найти вероятность того, что этот шар чёрный.
Равномерное распределение Распределение вероятностей непрерывной случайной величины X, принимающей все значения из отрезка [ a; b], называется равномерным, если её плотность вероятности на этом отрезке постоянна, а вне его равна нулю, т.е.
Так как
Определим математическое ожидание, дисперсию и среднее квадратическое отклонение для случайной величины с равномерным распределением.
Таким образом,
Таким образом, Пример. Все значения равномерно распределённой случайной величины лежат на отрезке [2;8]. Найти вероятность попадания случайной величины в промежуток (3;5). a=2, b=8, Биномиальное распределение
Пусть производится n испытаний, причём вероятность появления события A в каждом испытании равна p и не зависит от исхода других испытаний (независимые испытания). Так как вероятность наступления события A в одном испытании равна p, то вероятность его ненаступления равна q=1- p. Пусть событие A наступило в n испытаниях m раз. Это сложное событие можно записать в виде произведения:
Тогда вероятность того, что при n испытаниях событие A наступит m раз
или
Формула (1) называется формулой Бернулли. Пример. Пусть всхожесть семян данного растения составляет 90%. Найти вероятность того, что из четырёх посеянных семян взойдут: 1) три; 2) не менее трёх. 1) m=3, n=4, p=0,9, q=1-0,9=0,1,
2) P (A) =0,2916+0,6561=0,9477. Пусть X – случайная величина, равная числу появлений события A в n испытаниях, которая принимает значения
Полученный закон распределения случайной величины называется законом биномиального распределения.
Математическое ожидание, дисперсия и среднее квадратическое отклонение случайных величин, распределённых по биномиальному закону, определяются по формулам:
Пример. По мишени производятся три выстрела, причём вероятность попадания при каждом выстреле равна 0,8. Рассматривается случайная величина X – число попаданий в мишень. Найти её закон распределения, математическое ожидание, дисперсию и среднее квадратическое отклонение. p=0,8, q=0,2, n=3,
Получаем закон распределения:
Свойства функции Лапласа. 1. Доказательство: 2. Ф(x) – нечётная функция, т.е. Ф(- x)=-Ф(x). Доказательство:
3. Функция Ф( x) монотонно возрастает. Из формул (2) и (3) следует, что вероятность того, что случайная величина X примет значение из интервала
Пример. Случайная величина X распределена по нормальному закону. Математическое ожидание и среднее квадратическое отклонение этой величины соответственно равны 0 и 2. Найти вероятность того, что X примет значение, принадлежащее интервалу (-2;3).
Часто требуется вычислить вероятность того, что отклонение нормально распределённой случайной величины X от её математического ожидания по абсолютной величине меньше заданного положительного числа
Таким образом,
Пример. Пусть случайная величина X распределена по нормальному закону с параметрами
Нормальное распределение вероятностей имеет в теории вероятностей большое значение. В частности, закон распределения суммы достаточно большого числа независимых случайных величин, влияние каждой из которых на всю сумму ничтожно мало, близок к нормальному распределению. Этот факт получил название центральной предельной теоремы.
ЛЕКЦИЯ 1: «ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ» Понятие о случайном событии Опыт, эксперимент, наблюдение явления называется испытанием. Примеры: бросание монеты, бросание игральной кости. Результат, исход испытания называется событием. Примеры: выпадение герба, появление того или иного числа очков на брошенной игральной кости. Для обозначения событий используют большие буквы латинского алфавита: A, B, C и т.д. Определение 1. Два события называются совместимыми, если появление одного из них не исключает появление другого в одном и том же испытании. Пример. Испытание – однократное бросание игральной кости. Событие A – появление четырёх очков, событие B - появление чётного числа очков. Определение 2. Два события называют несовместимыми, если появление одного из них исключает появление другого в одном и том же испытании. Пример. Испытание – однократное бросание монеты. Событие A – выпадение герба, событие B - выпадение цифры. Определение 3. Два события A и B называются противоположными, если в данном испытании они несовместимы и одно из них обязательно происходит. Событие, противоположное событию A, обозначают через Определение 4. Событие называют достоверным, если в данном испытании оно является единственно возможным его исходом, и невозможным, если в данном испытании оно заведомо не может произойти. Определение 5. Событие называют случайным, если оно объективно может наступить или не наступить в данном испытании. Пример. Событие A – выпадение шести очков при бросании игральной кости – случайное. Можно ли как-то измерить возможность появления некоторого случайного события? Классическое определение вероятности Определение 1. Говорят, что совокупность событий образует полную группу событий для данного испытания, если его результатом обязательно становится, хотя бы одно из них. Примеры: попадание в цель или промах при одном выстреле; выпадение герба и выпадение цифры при одном бросании монеты. Определение 2. События Определение 3. Событие A называют благоприятствующим событию B, если наступление события A влечёт за собой наступление события B. Определение 4 (классическое определение вероятности). Вероятностью
Пример. Найти вероятность того, что при бросании игральной кости выпадет чётное число очков (событие A). n=6; m=3; Из классического определения вероятности вытекают следующие её свойства: 1. Вероятность достоверного события равна единице. Доказательство: m= n, тогда 2. Вероятность невозможного события равна нулю. Доказательство: m=0, тогда 3. Вероятность случайного события есть положительное число, заключённое между нулём и единицей. Доказательство:
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 107; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.118.99 (0.063 с.) |
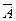 .
.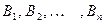 , образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события A:
, образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события A: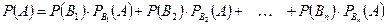 . (3)
. (3)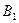 - выбор первого ящика;
- выбор первого ящика;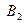 - выбор второго ящика;
- выбор второго ящика;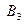 - выбор третьего ящика;
- выбор третьего ящика;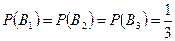 ;
; 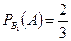 ;
; 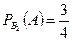 ;
; 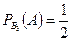 .
.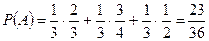 .
.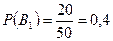 ;
; 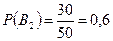 ;
; 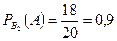 ;
; 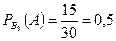 .
.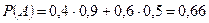 .
.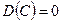
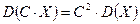
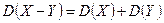
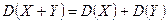
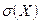 случайной величины X называется корень квадратный из её дисперсии:
случайной величины X называется корень квадратный из её дисперсии: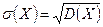 .
.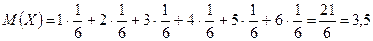 ;
;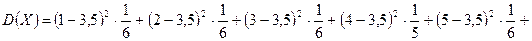
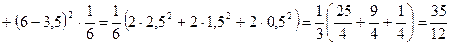 ;
;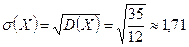 .
.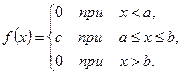
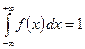 , получаем
, получаем 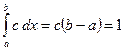 , отсюда
, отсюда 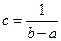 .
. Таким образом, плотность вероятности непрерывной случайной величины X, распределённой равномерно на отрезке [ a; b], имеет вид:
Таким образом, плотность вероятности непрерывной случайной величины X, распределённой равномерно на отрезке [ a; b], имеет вид: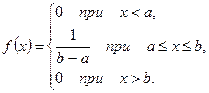
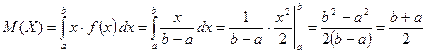 .
.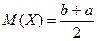 , как и должно, быть в силу симметрии распределения.
, как и должно, быть в силу симметрии распределения.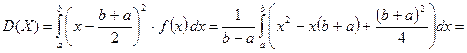
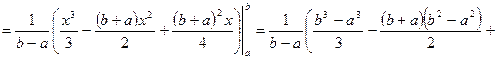

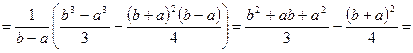
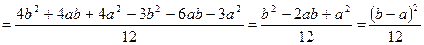 .
.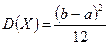 , тогда
, тогда 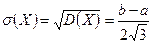 .
.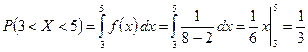 .
.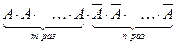 .
.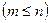 , вычисляется по формуле:
, вычисляется по формуле: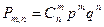
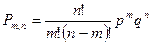 (1)
(1)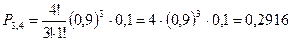 ;
;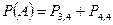 ,
, 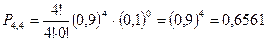 ;
;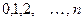 с вероятностями:
с вероятностями: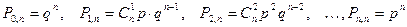 .
.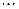
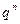
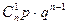
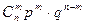
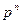
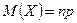 ,
, 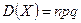 ,
, 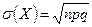 .
.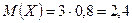 ,
, 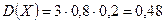 ,
, 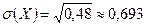 .
.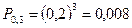 - вероятность 0 попаданий;
- вероятность 0 попаданий;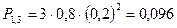 - вероятность одного попадания;
- вероятность одного попадания;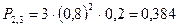 - вероятность двух попаданий;
- вероятность двух попаданий;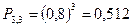 - вероятность трёх попаданий.
- вероятность трёх попаданий.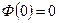 .
.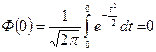 .
.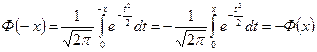 (замена t=- z, dt=- dz).
(замена t=- z, dt=- dz).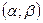 равна:
равна: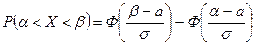 . (4)
. (4)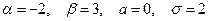 . По формуле (4) получаем:
. По формуле (4) получаем: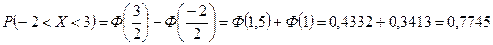 .
.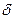 , т.е. найти
, т.е. найти 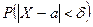 . По формуле (4) получаем:
. По формуле (4) получаем: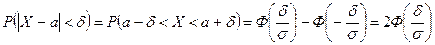 .
.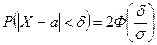 . (5)
. (5)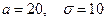 . Найти
. Найти 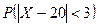 .
.
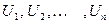 , образующие полную группу попарно несовместимых и равновозможных событий, будем называть элементарными событиями.
, образующие полную группу попарно несовместимых и равновозможных событий, будем называть элементарными событиями.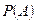 события A называют отношение
события A называют отношение  числа элементарных событий, благоприятствующих событию A, к числу всех элементарных событий, т.е.
числа элементарных событий, благоприятствующих событию A, к числу всех элементарных событий, т.е. 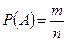 .
.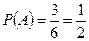 .
.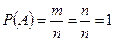 .
.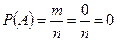 .
.