Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Гипербола, ее каноническое уравнение
Пусть снова имеются точки Определение. Гиперболой называется геометрическое место точек плоскости, модуль разности расстояний от каждой из которых до фокусов является постоянной величиной Обозначим произвольную точку гиперболы через
то уравнение гиперболы принимает вид
Далее приведем полученное уравнение к каноническому виду. С этой целью возведем дважды обе части равенства (5.6) в квадрат. Из определения гиперболы следует, что
Так как
Введем, как и выше, обозначение
и возведем в квадрат обе части равенства (5.6), получим уравнение
Или
После возведения в квадрат обеих частей последнего равенства получаем
или, после деления на (–4), Подставляя вместо
которое можно записать следующим образом:
Разность Разделив обе части последнего равенства на
Заметим, что в определении гиперболы также фигурируют два числа a, c, а в каноническом уравнении появляется b, связанное с ними по формуле (5.8). Найдем точки пересечения гиперболы (5.10) с осями координат: если Определение. Число а называется действительной полуосью гиперболы, а число b – ее мнимой полуосью. Определение. Асимптотой кривой называется прямая, расстояние до которой от точки, лежащей на кривой, стремится к нулю при неограниченном удалении от начала координат этой точки по кривой. Оказывается, гипербола имеет две наклонные пересекающиеся асимптоты с уравнениями
Определение. Эксцентриситетом гиперболы называется отношение фокусного расстояния Из (5.7) вытекает, что для гиперболы Частный случай. Если Полученная кривая имеет асимптоты Определение. Сопряженной к гиперболе (5.10) называется гипербола, заданная уравнением Нетрудно убедиться в том, что у сопряженной гиперболы
Сопряженная гипербола представляет собой кривую, состоящую из двух ветвей, симметричную относительно координатных осей и начала координат.
Рис. 5.4
|
|||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 115; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.236.62 (0.008 с.) |
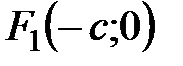 и
и 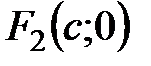 ,
, 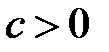 , называемые фокусами.
, называемые фокусами.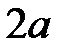 (
(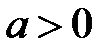 ), меньшей расстояния между фокусами
), меньшей расстояния между фокусами 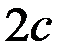 .
.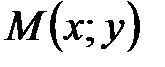 . Согласно определению гиперболы
. Согласно определению гиперболы 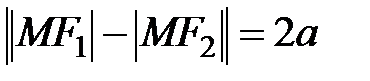 . Так как
. Так как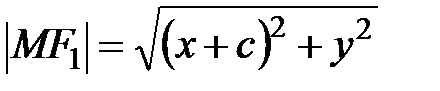 ,
, 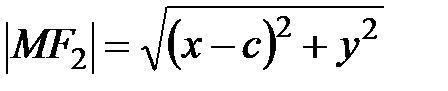 ,
,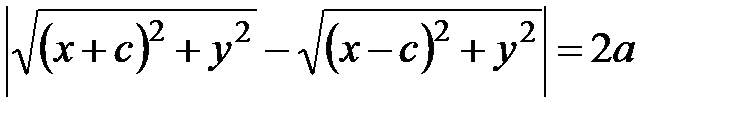 . (5.6)
. (5.6)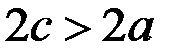 , поэтому
, поэтому . (5.7)
. (5.7)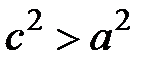 , то можно обозначить положительное число
, то можно обозначить положительное число 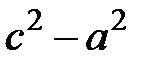 через
через 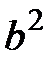 , откуда
, откуда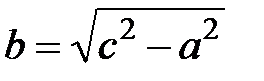 . (5.8)
. (5.8)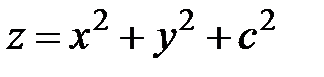 (5.9)
(5.9)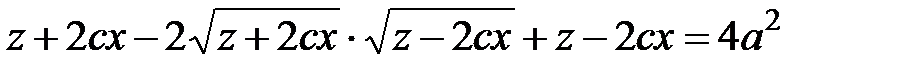 ,
,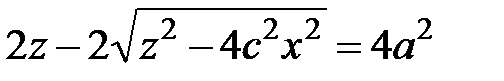 , которое запишем таким образом:
, которое запишем таким образом: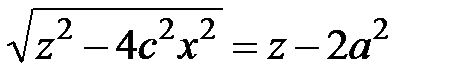 .
.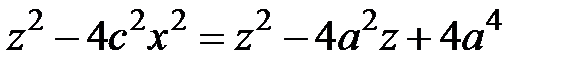 ,
,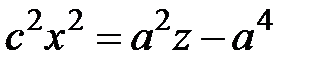 .
.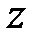 сумму из (5.9), приходим к равенству
сумму из (5.9), приходим к равенству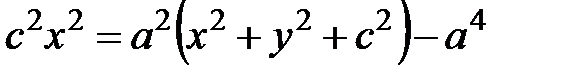 ,
,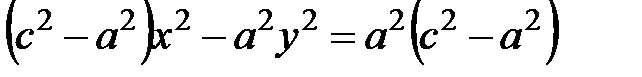 .
.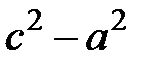 равна
равна 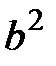 , значит, мы имеем
, значит, мы имеем 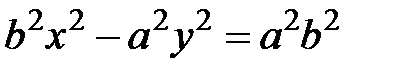 .
.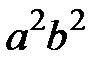 , приходим к каноническому уравнению гиперболы
, приходим к каноническому уравнению гиперболы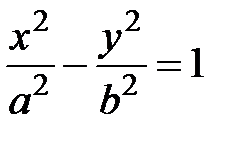 . (5.10)
. (5.10)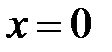 , то приходим к невозможному равенству
, то приходим к невозможному равенству 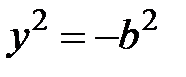 , если
, если 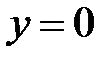 , то
, то 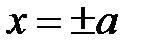 .
.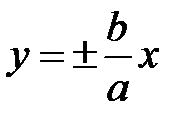 , проходящими через начало координат и симметричные относительно координатных осей.
, проходящими через начало координат и симметричные относительно координатных осей. 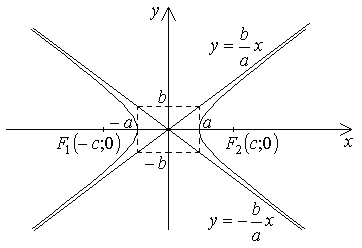 Гипербола представляет собой кривую, состоящую из двух ветвей, симметричную относительно координатных осей и начала координат.
Гипербола представляет собой кривую, состоящую из двух ветвей, симметричную относительно координатных осей и начала координат.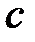 и действительной полуоси а, т.е.
и действительной полуоси а, т.е. 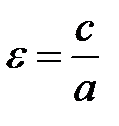 .
. 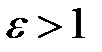 .
. , то
, то 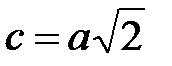 , и уравнение гиперболы принимает вид
, и уравнение гиперболы принимает вид 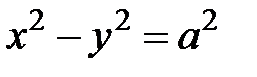 .
. 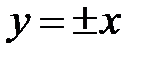 и называется равнобочной гиперболой.
и называется равнобочной гиперболой.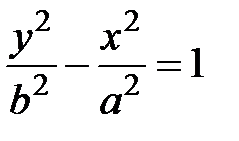 . (5.11)
. (5.11)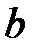 – действительная полуось, а асимптоты такие же, как у данной гиперболы:
– действительная полуось, а асимптоты такие же, как у данной гиперболы: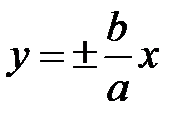 .
.