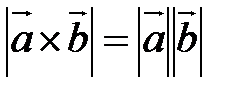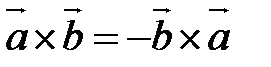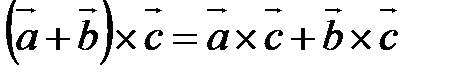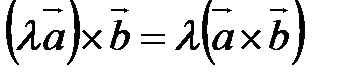Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача нахождения условия коллинеарности двух векторов
Установить условие коллинеарности векторов Так как векторы коллинеарны, то
Легко проверяется, что если координаты векторов удовлетворяют равенствам (3.6), то Равенства (3.6) называются условием коллинеарности двух векторов. Задача определения расстояния между двумя точками Пусть в пространстве
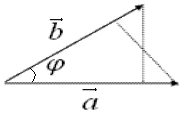
Рис. 2.16. Тогда и Так как длина вектора Заметим, что в процессе решения этой задачи установлена формула определения координат вектора, если заданы координаты его начальной и конечной точек: Скалярное произведение векторов Пусть даны два вектора Определение. Скалярным произведением векторов
Рис. 2.17. Так как откуда следует, что скалярное произведение векторов Свойства скалярного произведения векторов 1) 2) 3) 4) 5) Пусть векторы
Найдем скалярное произведение Имеем Итак, если векторы Следствие 1. Если Последнее называется условием перпендикулярности двух векторов. Следствие 2. Так как
Векторное произведение двух векторов Определение. Векторным произведением ненулевых и неколлинеарных векторов
2) вектор 3) направлен вектор Свойства векторного произведения 1. 2. Если 3. 4. 5.
Выражение векторного произведения двух векторов через
|
|||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 80; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.36.249 (0.01 с.) |
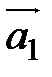 и
и 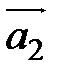 , если
, если 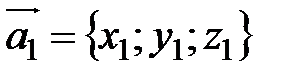 ,
, 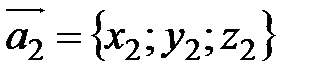 .
.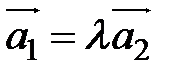 , где
, где 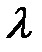 − некоторое число. Согласно (3.2) − (3.5) имеем
− некоторое число. Согласно (3.2) − (3.5) имеем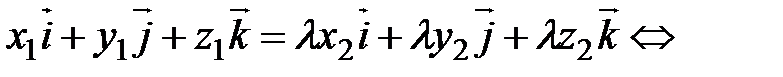
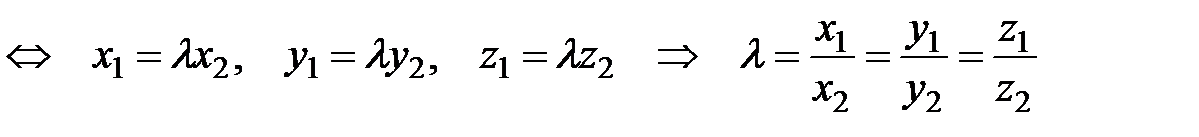 . (3.6)
. (3.6)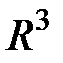 заданы своими координатами две точки
заданы своими координатами две точки 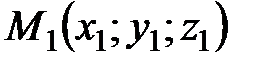 и
и 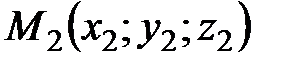 . Построим векторы
. Построим векторы 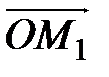 ,
, 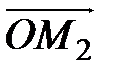 ,
, 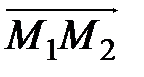 (рис. 2.16).
(рис. 2.16).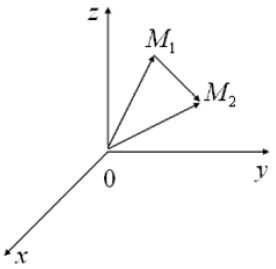
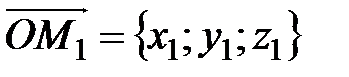 ,
, 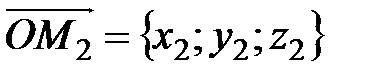 ,
, 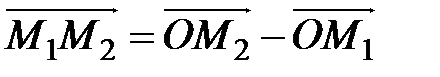
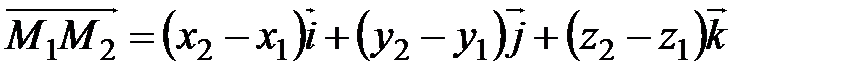 .
.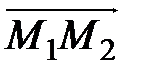 равна расстоянию между точками
равна расстоянию между точками 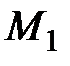 и
и 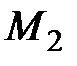 , то
, то 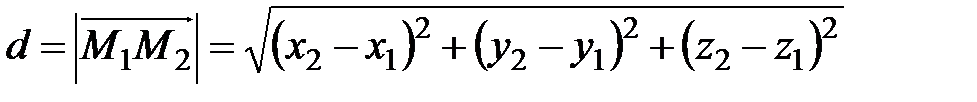 .
.  .
. 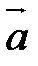 и
и 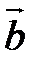 . В векторной алгебре рассматриваются два вида умножения векторов: скалярное, результатом которого является число, и векторное, результатом которого является вектор.
. В векторной алгебре рассматриваются два вида умножения векторов: скалярное, результатом которого является число, и векторное, результатом которого является вектор.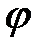 между ними (рис. 2.17). Скалярное произведение обозначается символом
между ними (рис. 2.17). Скалярное произведение обозначается символом 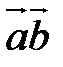 . Итак,
. Итак, 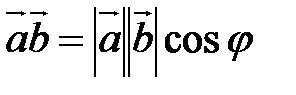 .
. 
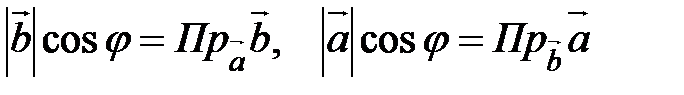 , то
, то 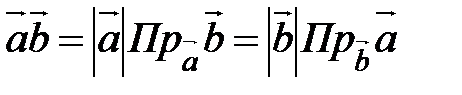 ,
, 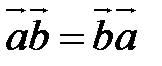 ;
;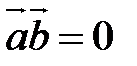 , если
, если 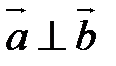 или хотя бы один из векторов есть нулевой вектор (справедливо и обратное утверждение);
или хотя бы один из векторов есть нулевой вектор (справедливо и обратное утверждение);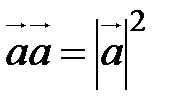 ;
;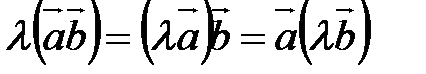 для
для 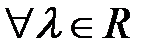 ;
;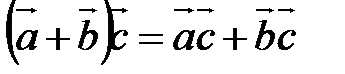 .
.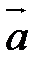 и
и 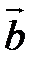 заданы своими координатами:
заданы своими координатами: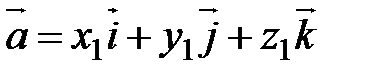 ,
, 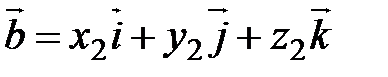 .
. . Вычислим предварительно скалярные произведения единичных векторов.
. Вычислим предварительно скалярные произведения единичных векторов.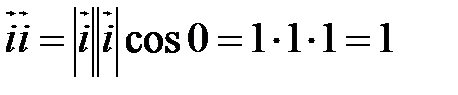 ,
, 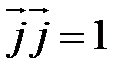 ,
, 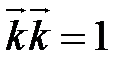 . Векторы
. Векторы 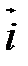 ,
, 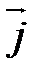 ,
, 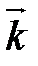 взаимно перпендикулярны. Тогда, согласно свойству 2, их произведения друг на друга равны нулю.
взаимно перпендикулярны. Тогда, согласно свойству 2, их произведения друг на друга равны нулю.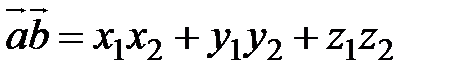 .
. 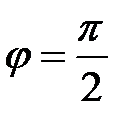 , то
, то 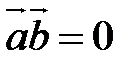 или
или 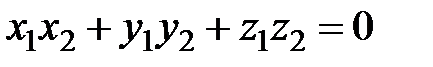 .
. 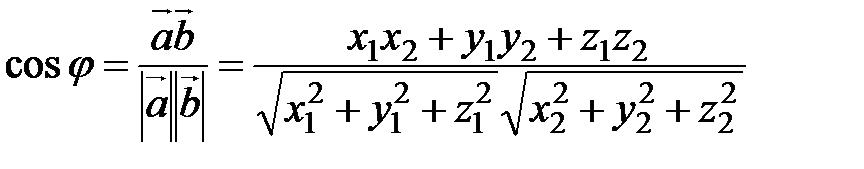 .
.  и
и  называется вектор, обозначаемый символом
называется вектор, обозначаемый символом 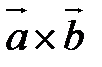 , который определяется следующими тремя условиями:
, который определяется следующими тремя условиями: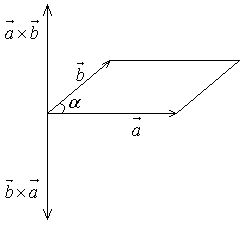 1) модуль вектора
1) модуль вектора 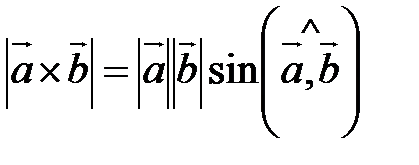 ;
;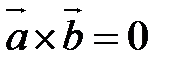 , если
, если 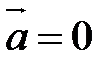 , или
, или 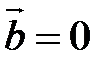 , или
, или 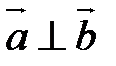 , то
, то