
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Координаты векторов сомножителей
Если Геометрический смысл модуля векторного произведения
Смешанное произведение векторов Пусть даны три вектора Рассмотрим подробно произведение называемое смешанным. Это. произведение, в котором вначале находится векторное произведение двух из заданных векторов, а затем скалярное произведение полученного вектора на третий из данных векторов. Например, вначале находится векторное произведение Смешанное или иначе векторно-скалярное произведение обозначается символом Пусть требуется определить смешанное произведение векторов, если известны координаты этих векторов
или Формула дает выражение для смешанного произведения в координатной форме. Заметим, что в этой формуле координаты векторов Для смешанного произведения векторов справедливы равенства
Проверим, например, справедливость равенства Итак,
Следствие (условие компланарности трех векторов). Для того, чтобы три вектора
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ Аналитическая геометрия на плоскости Прямая линия Из школьного курса математики известно, что в декартовой системе координат прямая линия может задаваться одним из уравнений:
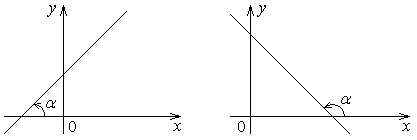
Первое равенство является уравнением вертикальной прямой линии, проходящей через точку Будем обозначать прямые строчными латинскими буквами (возможно с нижними индексами). Определение .Углом наклона
Рис. 4.1 Определение .Угловым коэффициентом невертикальной прямой В действительности угловой коэффициент прямой Теперь положим Определение. Уравнение прямой вида (4.2) называется уравнением прямой с угловым коэффициентом. Замечание 4.1. Если задан угловой коэффициент
Действительно, при Уравнение прямой,
|
|||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 98; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.136.22.50 (0.007 с.) |
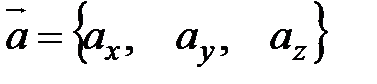 ,
,  , то
, то 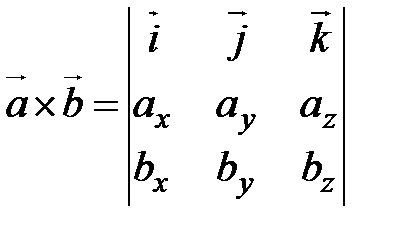 .
.  параллелограмма
параллелограмма 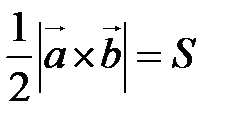 треугольника
треугольника 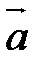 ,
, 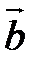 ,
,  . Так как для векторов введены два вида произведений – скалярное и векторное, то для трех векторов относительно операции умножения существуют разные виды произведений.
. Так как для векторов введены два вида произведений – скалярное и векторное, то для трех векторов относительно операции умножения существуют разные виды произведений.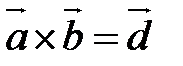 , затем – скалярное произведение
, затем – скалярное произведение 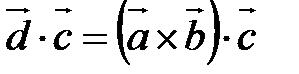 .
.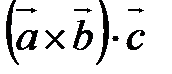 или символом
или символом  . Результатом смешанного произведения является число.
. Результатом смешанного произведения является число.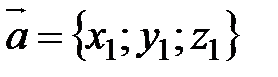 ,
, 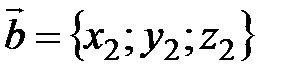 ,
,  . Вычислим предварительно
. Вычислим предварительно 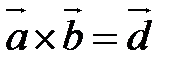 . Имеем
. Имеем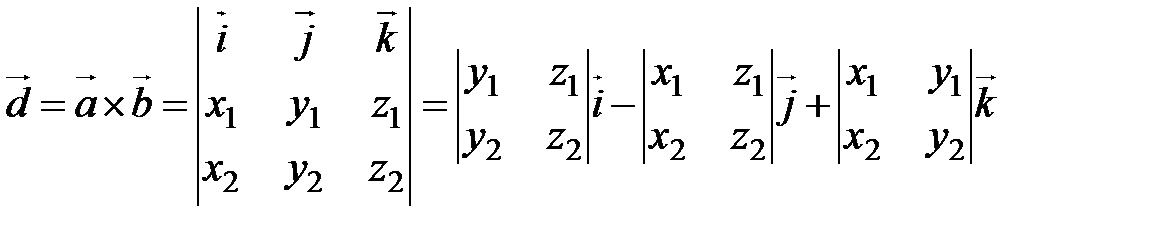
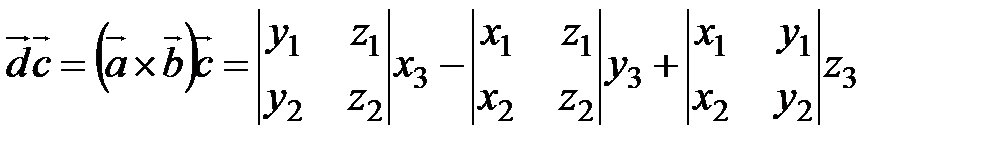 . Полученное равенство, согласно теореме о разложении определителя по элементам строки, можно переписать в форме
. Полученное равенство, согласно теореме о разложении определителя по элементам строки, можно переписать в форме 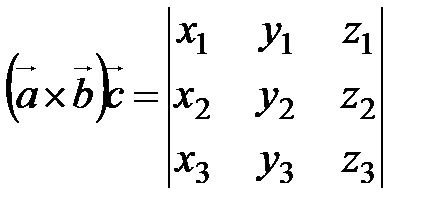 .
. 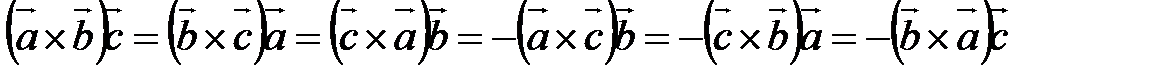 .
. . Согласно формуле) имеем
. Согласно формуле) имеем 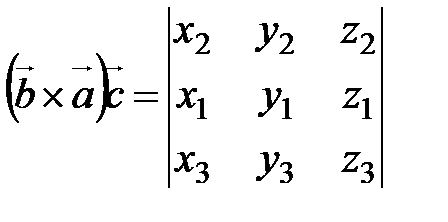 . Как известно, при перестановке двух срок определителя знак определителя меняется на противоположный. Тогда, умножая обе части предыдущего равенства на (−1), получим
. Как известно, при перестановке двух срок определителя знак определителя меняется на противоположный. Тогда, умножая обе части предыдущего равенства на (−1), получим 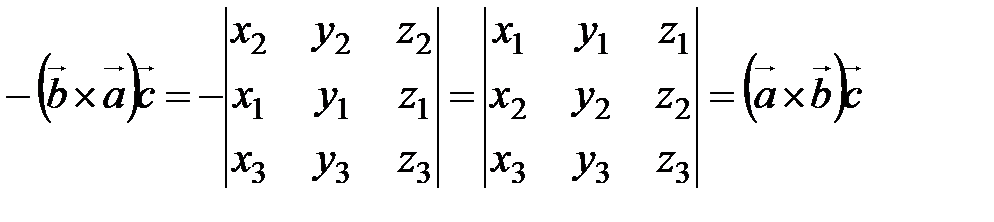 .
.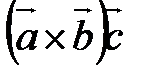 равен объему параллелепипеда, построенного на этих векторах как на ребрах.
равен объему параллелепипеда, построенного на этих векторах как на ребрах.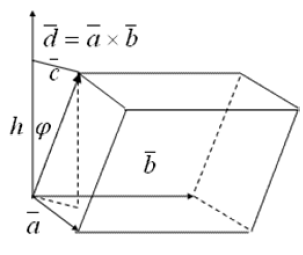
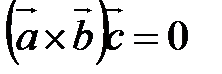 или в координатной форме
или в координатной форме  .
. 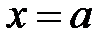 , (4.1)
, (4.1)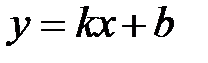 . (4.2)
. (4.2)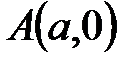 и параллельной оси
и параллельной оси 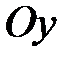 . Второе уравнение задает линейную функцию, графиком которой является невертикальная прямая. Напомним геометрический смысл параметров
. Второе уравнение задает линейную функцию, графиком которой является невертикальная прямая. Напомним геометрический смысл параметров 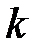 и
и 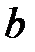 , входящих в уравнение (4.2).
, входящих в уравнение (4.2).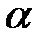 прямой
прямой 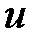 к оси
к оси 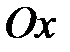 называется угол, откладываемый против часовой стрелки от положительного направления оси
называется угол, откладываемый против часовой стрелки от положительного направления оси 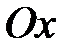 до прямой
до прямой 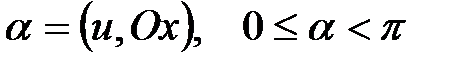 .
. 
 в уравнении (4.2), т.е.
в уравнении (4.2), т.е. 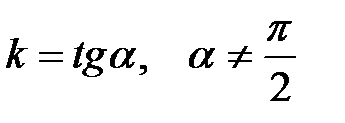 .
. 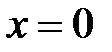 в уравнении (4.2), получим
в уравнении (4.2), получим 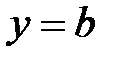 . Геометрически это означает, что число
. Геометрически это означает, что число 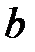 – ордината точки пересечения прямой с осью
– ордината точки пересечения прямой с осью  .
.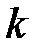 прямой
прямой 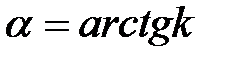 если
если 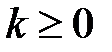 ,
, 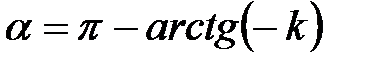 если
если 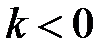 ,
, 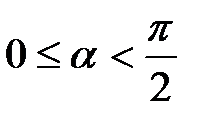 уравнение
уравнение 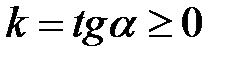 эквивалентно уравнению
эквивалентно уравнению 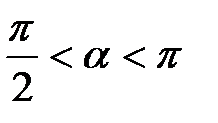 , то
, то 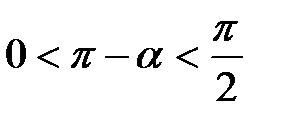 и, значит,
и, значит, 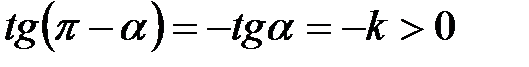 , откуда находим, что
, откуда находим, что 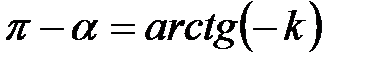 , или
, или 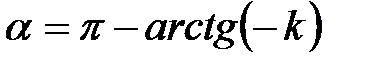 .
.


