
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение вырожденных систем линейных уравнений.Стр 1 из 5Следующая ⇒
ЛИНЕЙНАЯ АЛГЕБРА
Методические указания для самостоятельной работы студентов по направлению подготовки 38.03.01 – Экономика
Воронеж 2016
УДК 512.8
Раецкая, Е. В. Линейная алгебра [Текст]: методические указания к практическим занятиям для студентов по направлению подготовки 38.03.01 – Экономика / Е. В. Раецкая, И.В. Сапронов, Н.М. Спирина; М-во образования и науки РФ, ФГБОУ ВО «ВГЛТУ». – Воронеж, 2016. – 46 с.
Печатается по решению учебно-методического совета ФГБОУ ВО «ВГЛТУ» (протокол № 5 от 22 апреля 2016 г.)
Рецензент д-р физ.-мат. наук, доцента кафедры математического анализа ВГУ Зубова С.П.
Содержание Введение……………………………………………………………………………4 1.Матрицы и определители………………………………………………………5 2.Системы линейных уравнений ………………………………………………10 3. Векторная алгебра ……………………………………………………………..15 4. Аналитическая геометрия…………………………………………………….28 5. Кривые второго порядка……………………………………………………..36
Вопросы для контроля. ………………………………………………………….44
Библиографический список…………………………………………………...45 Введение
Целью изучения дисциплины «Линейная алгебра» является воспитание достаточно высокой математической культуры, привитие навыков современных видов математического мышления, обучение основным математическим понятиям и методам линейной алгебры, необходимым для анализа и моделирования устройств, процессов и явлений при поиске оптимальных решений практических задач, методам обработки и анализа результатов численных экспериментов для экономических задач. Для достижения поставленной цели, при самостоятельной работе решаются следующие задачи: - самостоятельное усвоение студентом теоретического материала, построенного на основе четких формулировок и доказательстве основных теорем и выработка умения самостоятельно иллюстрировать его примерами и задачами; самостоятельное изучение истории появления наиболее важных понятий и результатов; наряду с изучением основных теоретических результатов при самостоятельной работе с учебными материалами, необходимо обращать внимание на пояснения об их приложениях к другим разделам математики и к техническим наукам;
- закрепление теоретического материала и выработка умения самостоятельно применять математические методы в различных приложениях. В результате самостоятельного освоения дисциплины студент должен: - знать основные понятия, определения и методы исследования объектов с помощью теорем и формул различных разделов курса математики; - уметь: четко формулировать и доказывать основные положения курса математики, решать задачи и примеры по различным разделам высшей математики с доведением решения до практического приемлемого результата (формулы, числа, графика, качественного вывода и т.п.), уметь при решении задач самостоятельно выбирать необходимые вычислительные методы и средства (ПЭВМ, таблицы и справочники); самостоятельно изучать научную литературу по математике; - иметь представление о численных алгоритмах решения математических и прикладных задач его профессиональной области. Студент по результатам освоения дисциплины «Линейная алгебра» должен обладать способностью выбрать инструментальные средства для обработки экономических данных в соответствии с поставленной задачей, проанализировать результаты расчетов и обосновать полученные выводы.
МАТРИЦЫ И ОПРЕДЕЛИТЕЛИ Матрицей А размера
Часто для краткости пишу
Элементы Матрица A, состоящая из одной строки называется строкой (вектор-строкой), матрица, состоящая из одного столбца называется столбцом (вектор-столбец). Матрица, получающаяся из матрицы A заменой строк столбцами называется транспонированной матрицей по отношению к матрице A и обозначается
Если матрица А имеет размер Суммой двух матриц одинакового размера
Нулевой матрицей 0 называется матрица, все элементы которой равны нулю. Легко проверить, что выполнены следующие свойства для операции сложения матриц: 1. А+В=В+А (коммутативность), 2. (А+В)+С=А+(В+С) (ассоциативность), 3. А+0=А. Произведением матрицы размера Произведением матриц АВ называется матрица
Иначе говоря, элемент cij равен сумме произведений элементов i-ой строки матрицы А на соответствующий элемент j-ого столбца матрицы В. С помощью знака суммирования можно записать это так:
Единичной матрицей порядка
Каждой квадратной матрице можно сопоставить некоторое число, называемое определителем матрицы и обозначаемое через |A| или Определителем матрицы 2-го порядка называется число Определителем матрицы 3-го порядка называется число Общее понятие определителя дадим с помощью рекуррентной схемы, а именно, считая, что понятие определителя известно для матриц п–1-го порядка, дадим его для матриц п-го порядка (фактически так и вводилось понятие определителя для матриц 3-го порядка).Определителем матрицы Определитель матрицы Основные свойства определителей. 1. Определитель матрицы и транспонированной матрицы не изменяется т.е.
2. Общий множитель в строке или столбце можно вынести за знак определителя, т.е.
3. Определитель, имеющий нулевую строку или нулевой столбец, равен нулю:
4. Определитель, имеющий две равные строки или два равных столбца, равен нулю:
5. Определитель, две строки или два столбца которого пропорциональны, равен нулю:
6. При перестановке двух строк или двух столбцов определителя он умножается на –1:
7. 8. Величина определителя не изменится, если к элементам одной строки прибавить соответствующие элементы другой строки, умноженные на одно и то же число:
Квадратная матрица называется невырожденной, если ее определитель отличен от нуля. Пусть дана матрица Выберем k строк и k столбцов в этой матрице и составим новую матрицу из элементов, стоящих на пересечении этих строк и столбцов. Определитель полученной матрицы называется минором порядка k. Например, если выбрать вторую и третью строки, первый и третий столбец, то получим минор второго порядка Рангом матрицы называется максимальный порядок ее миноров, отличных от нуля.
Алгебраическим дополнением Обозначим через Квадратная матрица Для существования обратной матрицы необходимо и достаточно, чтобы исходная матрица была невырожденной. Тогда
то есть ее элементами являются алгебраические дополнения к элементам транспонированной матрицы
СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ Линейным алгебраическим уравнением называется уравнение вида
где Таким образом, в левой части линейного уравнения стоит линейная комбинация неизвестных, а в правой – число. Линейное уравнение называется однородным, если b = 0. В противном случае уравнение называется неоднородным. Системой линейных алгебраических уравнений называется система вида
где Решением системы линейных алгебраических уравнений называется набор чисел Система линейных алгебраических уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет решений. Совместная систем линейных алгебраических уравнений называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения. Имеется три основных способа решения систем линейных уравнений. Первым является метод Гаусса последовательного исключения переменных. Два других способа – метод обратной матрицы и правило Крамера. Определение. Матрицы
называются соответственно матрицей и расширенной матрицей системы (2.1). Если ранг матрицы А равен рангуматрицы А 1, то система совместна. Исследование на совместность и решение системы производят обычно одновременно с помощью метода Гаусса. Напомним, что элементы аii в матрице А называются диагональными.
Метод Гаусса заключается в преобразованиях строк матрицы А 1 так, чтобы элементы преобразованной матрицы, стоящее ниже диагональных элементов, были нулевыми. При этом необходимо следить за диагональными элементами: они не должны обращаться в нуль. Если же при преобразованиях строк какой-либо диагональный элемент обратится в нуль (например, а ii = 0), то поступать необходимо следующим образом: а) если в этом же столбце (где диагональный элемент оказался равен нулю) имеется ниже диагонального элемента ненулевой элемент, то соответствующую строку меняют местом с i -й строкой и продолжают преобразования; б) если же ниже нулевого диагонального элемента все элементы нулевые, то мы должны перейти к построению ступенчато-диагональной матрицы. Для этого сдвигаемся на один столбец вправо и считаем, что и диагональ матрицы тоже сдвинулась вправо, и далее поступаем как описано выше. После всех преобразований матрица системы должна принять так называемый диагонально ступенчатый вид:
Рассмотрим систему линейных алгебраическихуравнений, в которой число уравнений равно числу неизвестных:
Для нахождения решения совместной определенной системы уравнений, в которой число уравнений совпадает с числом неизвестных, можно применять метод обратной матрицы и метод Крамера. Рассмотрим систему линейных алгебраическихуравнений (2.2) и введем следующие обозначения:
Тогда систему (2.2) можно записать в виде матричного уравнения: АХ = В. (2.3) Пусть матрица А – невырожденная, тогда существует обратная к ней матрица Умножим обе части равенства () слева на Получим Итак, решением матричного уравнения (2.3) является произведение матрицы, обратной к А, на столбец свободных членов системы (2.2). Система решена методом обратной матрицы. Назовем главным определителем системы (2.2) определитель
а определителем (система является совместной, определенной). Приведенные формулы и называются формулами Крамера. Отметим, что если
Если ВЕКТОРНАЯ АЛГЕБРА Пусть даны две точки А и В. Отрезок, соединяющий эти точки, будем называть направленным, если указаны начальная и конечная точка отрезка, т.е. на отрезке указано направление.
Вектором называется направленный отрезок. Векторы принято обозначать буквами а, b, c, …, или
Вектор называется нулевым, если начальная и конечная точки совпадают. В этом случае будем писать а = Векторы а и b называются коллинеарными (при этом пишут a || b), если существует прямая которой они параллельны. Нулевой вектор считается коллинеарным любому вектору. Два вектора называются равными, если они коллинеарны, одинаково направлены и имеют равные длины. Иными словами, мы рассматриваем свободные векторы, начальные точки которых могут выбираться произвольным образом. Сложение векторов. Пусть даны векторы а и b. Совместим начальную точку вектора b с конечной точкой вектора а. Тогда вектор, начальная точка которого совпадает с начальной точкой вектора а, а конечная – с конечной точкой b, называется суммой векторов а + b.
Совместим начальные точки векторов а и b и обозначим эту точку через О. Построим параллелограмм ОАСВ на сторонах этих векторов. Тогда вектор
Видно, что Имеет место также свойство ассоциативности: (а + b) + c = a + (b + c). Умножение вектора на число. Определение. Пусть даны вектор Следствие 1. Из определения умножения вектора на число следует, что если Следствие 2. Противоположный вектор 1. ( 2. 3. Вычитание векторов. Разностью двух векторов а и b называется вектор a – b = a + (-1)·b. Зафиксируем в пространстве некоторую точку О и три взаимно перпендик-улярных вектора единичной длины i, j и k. Совокупность точки О и векторов i, j, k называется декартовой прямоугольной системой координат.
Числа x1, y1, z1 в представлении называются координатами вектора а. Вместе с равенством будет использоваться также запись вида a = (x1, y1, z1). Радиусом-вектором точки А называется вектор, начало которого совпадает с началом координат О, а конец – с точкой А. Координатами точки А называются координаты радиус-вектора точки А. При этом, если Пример. Найдем координаты вектора В = { x2, y2, z2}. Имеем
. Пусть заданы векторы Углом между векторами
Пусть в пространстве заданы вектор
Обозначим через Проекцией вектора Выберем на оси Проекция вектора Если Итак, для любых углов Если вектор АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ Прямая линия Из школьного курса математики известно, что в декартовой системе координат прямая линия может задаваться одним из уравнений:
Первое равенство является уравнением вертикальной прямой линии, проходящей через точку Будем обозначать прямые строчными латинскими буквами (возможно с нижними индексами). Определение .Углом наклона
Рис. 4.1 Определение .Угловым коэффициентом невертикальной прямой В действительности угловой коэффициент прямой Теперь положим Определение. Уравнение прямой вида (4.2) называется уравнением прямой с угловым коэффициентом. Замечание 4.1. Если задан угловой коэффициент
Действительно, при Уравнение прямой, Угол между прямыми Пусть даны две прямые Определение. Углом
Вычисление угла
Вычисление Для ее доказательства предположим, что прямые ВОПРОСЫ ДЛЯ КОНТРОЛЯ 1.Матрицы и действия с ними. 2.Симметрическая, диагональная, единичная матрицы. 3. Ортогональная матрица. 4. Обратная матрица. 5. Ранг матрицы. 6. Определители второго и третьего порядков. 7. Определители n-го порядка. 8. Определители n-го порядка и их свойства. 9. Алгебраические дополнения и миноры. 10. Вычисление определителей разложением по столбцу или по строке. 11. Системы линейных алгебраических уравнений. 12. Методы решения систе
|
|||||||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 149; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.127.232 (0.149 с.) |
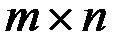 называется таблица из
называется таблица из 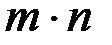 чисел
чисел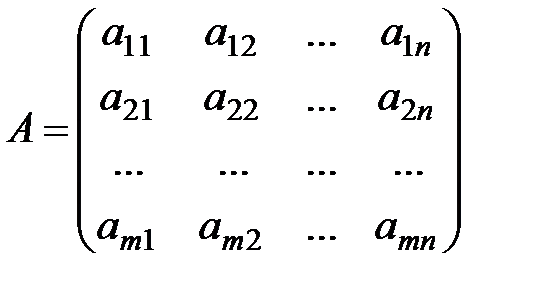
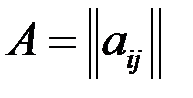 . Числа, из которых состоит матрица, называются элементами матрицы. Индексы у элементов матрицы указывают расположение этого элемента в таблице: первый индекс – номер строки, в которой находится элемент, а второй – номер столбца. Например, элемент
. Числа, из которых состоит матрица, называются элементами матрицы. Индексы у элементов матрицы указывают расположение этого элемента в таблице: первый индекс – номер строки, в которой находится элемент, а второй – номер столбца. Например, элемент 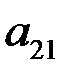 находится на пересечении второй строки и первого столбца:
находится на пересечении второй строки и первого столбца: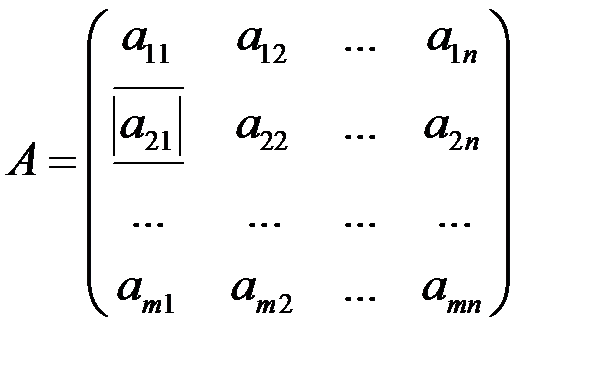
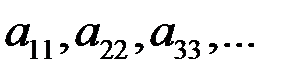 называются элементами главной диагонали матрицы или просто главной диагональю матрицы.
называются элементами главной диагонали матрицы или просто главной диагональю матрицы.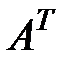 , элементы транспонированной матрицы и исходной связаны соотношением
, элементы транспонированной матрицы и исходной связаны соотношением 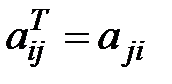 .
.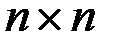 , то такую матрицу называют квадратной матрицей порядка
, то такую матрицу называют квадратной матрицей порядка 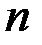 . Две матрицы одинакового размера
. Две матрицы одинакового размера 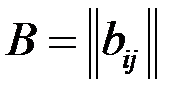 называют равными (при этом пишут А = В), если
называют равными (при этом пишут А = В), если 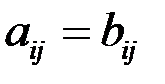 ,
, 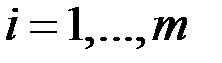 ;
; 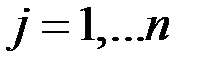 . (т.е., если у них соответственно равны элементы, стоящие на одинаковых местах в таблице).
. (т.е., если у них соответственно равны элементы, стоящие на одинаковых местах в таблице).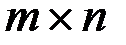
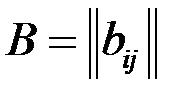 называют матрицу
называют матрицу 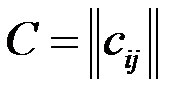 размера
размера 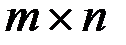 такую, что
такую, что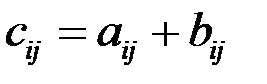 ,
, 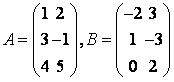
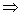
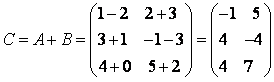 .
.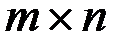
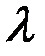 называют матрицу того же размера
называют матрицу того же размера 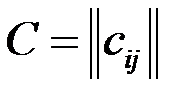 такую, что
такую, что 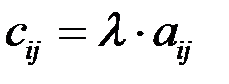
 на матрицу
на матрицу 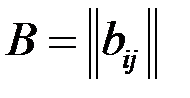 размера
размера 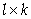 определено лишь для случая, когда число столбцов матрицы А совпадает с числом строк матрицы В, т.е. когда n=l. В этом случае произведение матриц определяется следующим образом:
определено лишь для случая, когда число столбцов матрицы А совпадает с числом строк матрицы В, т.е. когда n=l. В этом случае произведение матриц определяется следующим образом: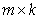 , у которой
, у которой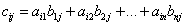 ,
, 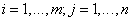
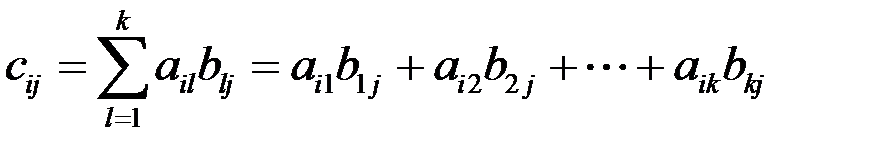
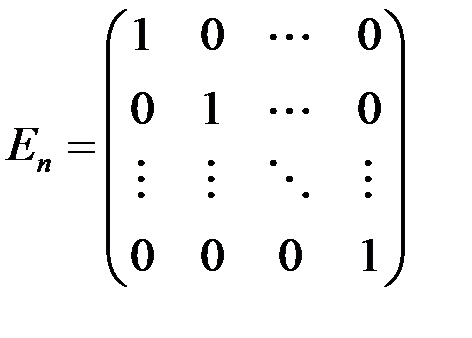 .
.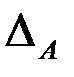 Прежде чем дать общее определение этого понятия, определим его для матриц 2-го и 3-го порядков.
Прежде чем дать общее определение этого понятия, определим его для матриц 2-го и 3-го порядков.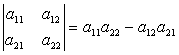 .
.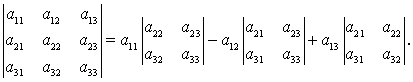
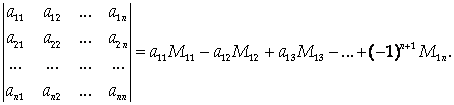
 принято обозначать
принято обозначать 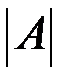 , или
, или 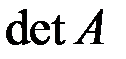 .
.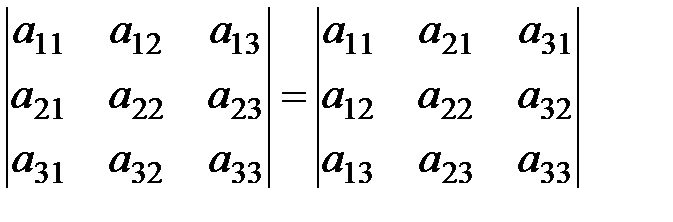
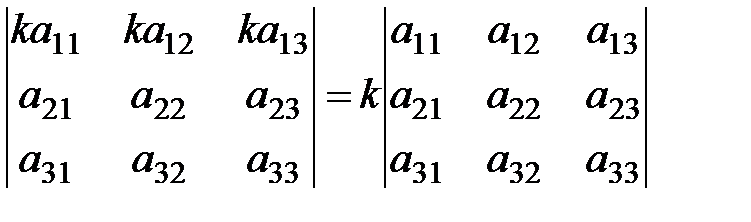
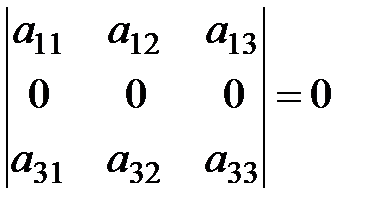
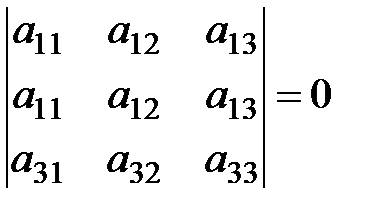
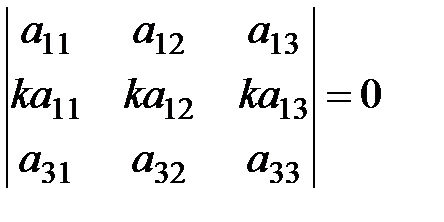
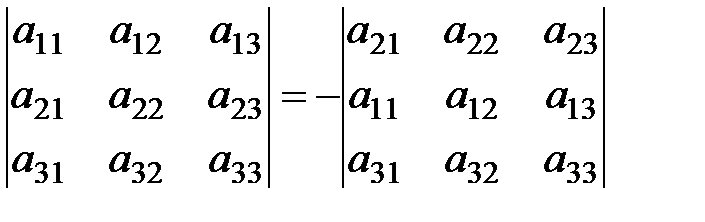
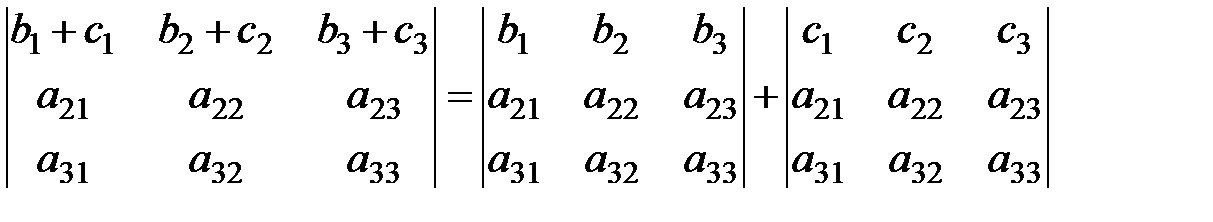
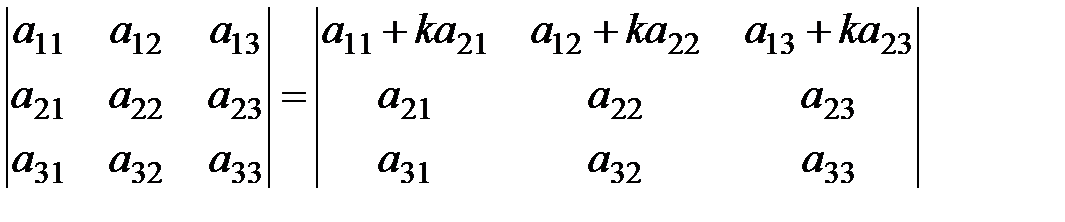

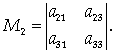
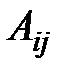 элемента определителя называется его минор, если сумма индексов данного элемента
элемента определителя называется его минор, если сумма индексов данного элемента 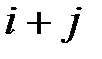 есть число четное, или число, противоположное минору, если
есть число четное, или число, противоположное минору, если 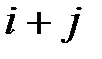 нечетно, т.е.
нечетно, т.е. 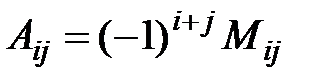 .
.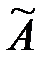 матрицу, составленную из алгебраических дополнений матрицы
матрицу, составленную из алгебраических дополнений матрицы 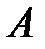 .
.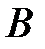 называется обратной к квадратной матрице
называется обратной к квадратной матрице 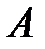 того же порядка, если
того же порядка, если 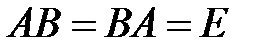 . При этом
. При этом 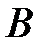 обозначается
обозначается 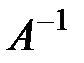 .
.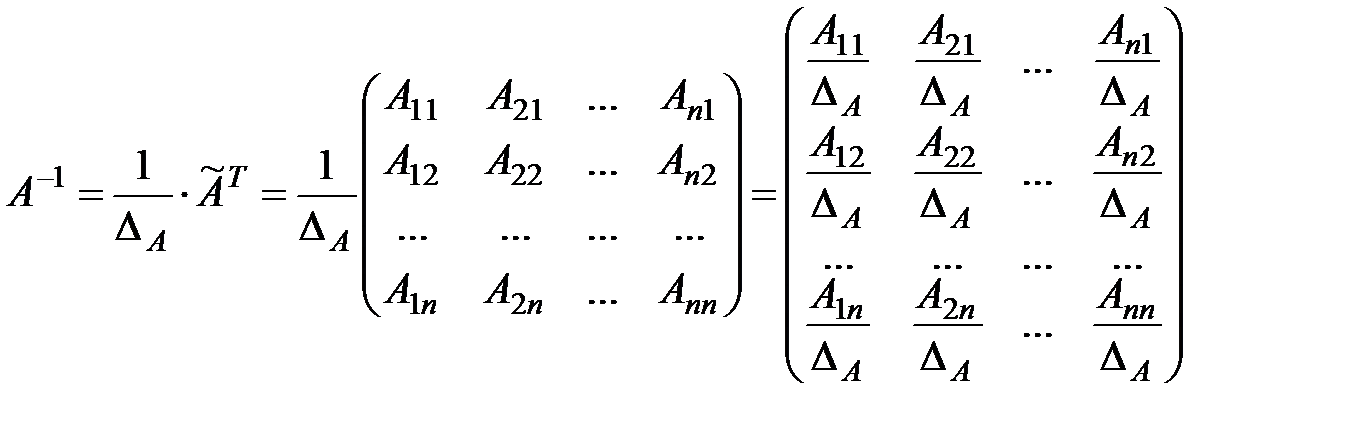 ,
,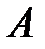 , деленные на ее определитель. Отметим, что обратная матрица
, деленные на ее определитель. Отметим, что обратная матрица 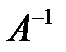 определена однозначно т.е. существует только одна обратная матрица для заданной квадратной невырожденной матрицы
определена однозначно т.е. существует только одна обратная матрица для заданной квадратной невырожденной матрицы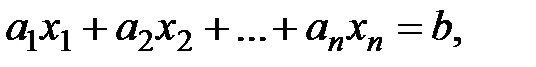
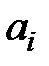 и b – числа,
и b – числа, 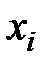 - неизвестные.
- неизвестные.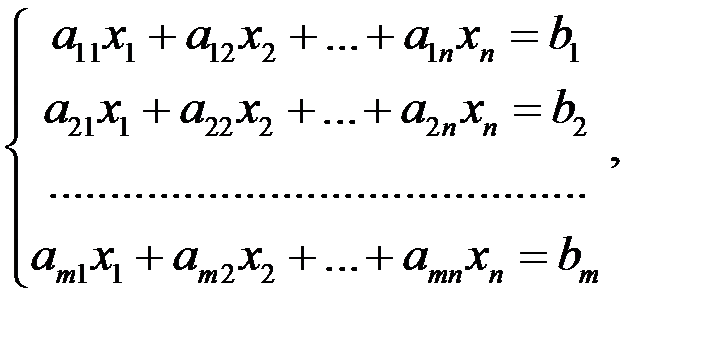 (2.1)
(2.1)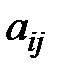 ,
, 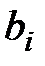 - числа,
- числа, 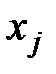 - неизвестные,
- неизвестные, 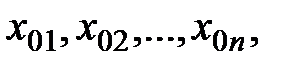 которые при подстановке вместо неизвестных обращают каждое уравнение системы в верное равенство.
которые при подстановке вместо неизвестных обращают каждое уравнение системы в верное равенство.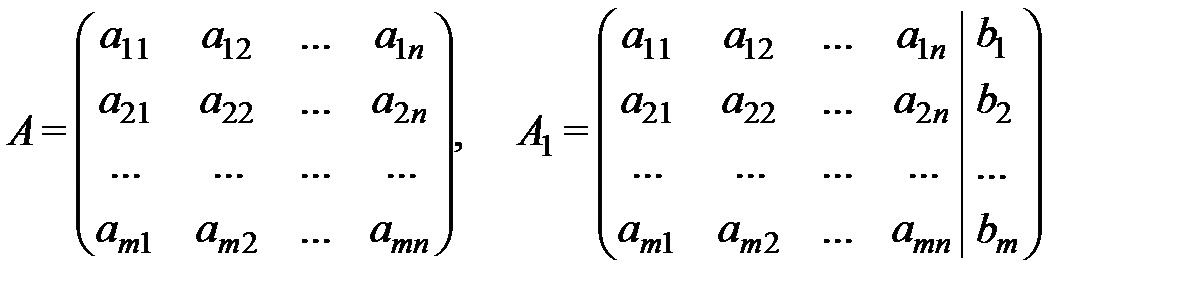


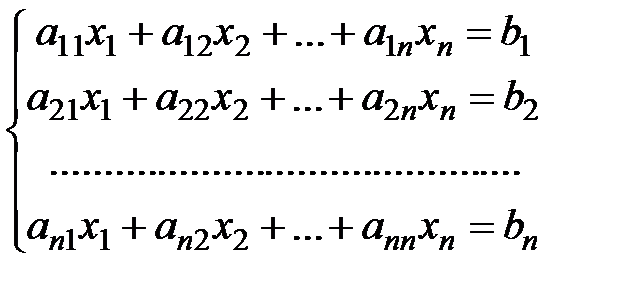 (2.2)
(2.2) 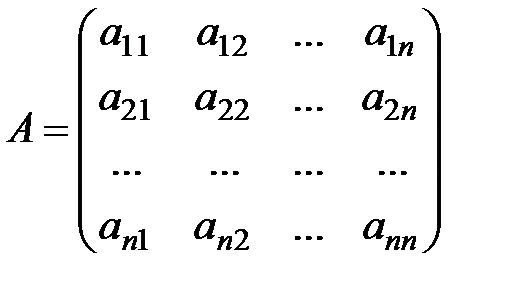 - матрица системы,
- матрица системы,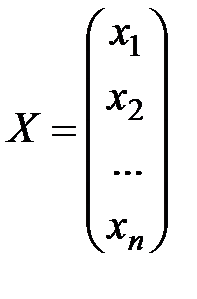 - столбец неизвестных,
- столбец неизвестных, 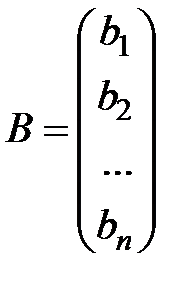 - столбец свободных членов.
- столбец свободных членов.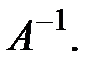
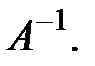
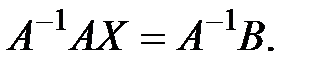 Но
Но 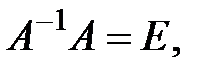 тогда
тогда 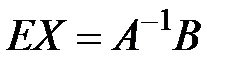 , а поскольку
, а поскольку 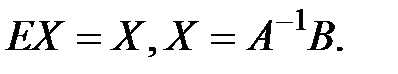
 , элементами которого являются коэффициенты при неизвестных:
, элементами которого являются коэффициенты при неизвестных: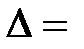
 , (2.4)
, (2.4)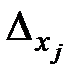 - определитель, полученный из (2.4) заменой столбца коэффициентов при xj на столбец свободных членов. Тогда, если
- определитель, полученный из (2.4) заменой столбца коэффициентов при xj на столбец свободных членов. Тогда, если 
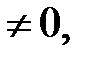 то система (2.2) имеет единственное решение, определяемое по формулам:
то система (2.2) имеет единственное решение, определяемое по формулам: 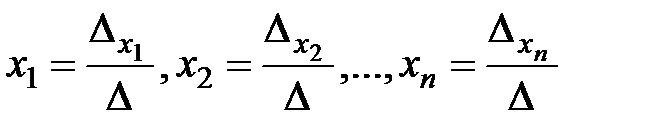
 =
= 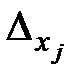 =0, то система имеет бесконечно много решений (система является совместной, неопределенной).
=0, то система имеет бесконечно много решений (система является совместной, неопределенной). = 0, а хотя бы один из
= 0, а хотя бы один из 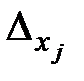
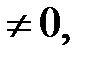 то система не имеет решений (система является несовместной).
то система не имеет решений (система является несовместной).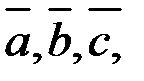 …, или
…, или 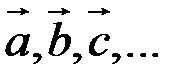 , или
, или  указывая начальные и конечные точки.
указывая начальные и конечные точки.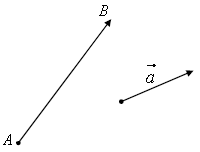
 . Длиной вектора называется длина соответствующего ему направленного отрезка. Длина обозначается через | a | или
. Длиной вектора называется длина соответствующего ему направленного отрезка. Длина обозначается через | a | или 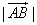 .
.
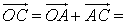 a + b. Тем самым получено эквивалентное определение суммы векторов, называемое правилом параллелограмма.
a + b. Тем самым получено эквивалентное определение суммы векторов, называемое правилом параллелограмма.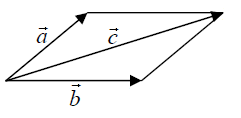
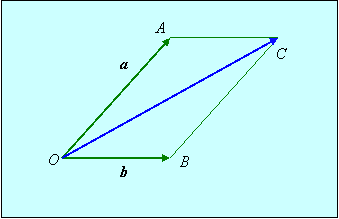
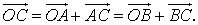 Таким образом, операция сложения векторов коммутативна: a + b = b + a.
Таким образом, операция сложения векторов коммутативна: a + b = b + a.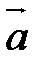 и число
и число 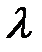 . Произведением вектора
. Произведением вектора 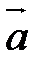 на число
на число 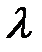 называется вектор
называется вектор 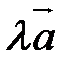 , коллинеарный вектору
, коллинеарный вектору 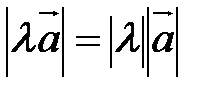 и то же направление, что и вектор
и то же направление, что и вектор 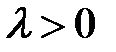 , и противоположное направление, если
, и противоположное направление, если 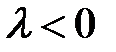 . Если
. Если 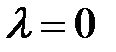 , то
, то 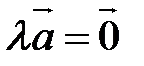 .
.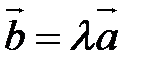 , то векторы
, то векторы 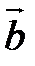 и
и 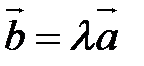 . Таким образом, два вектора
. Таким образом, два вектора 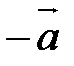 можно рассматривать как произведение вектора
можно рассматривать как произведение вектора 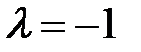 , то есть
, то есть 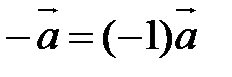 . Отметим основные свойства операции умножения вектора на число, которые непосредственно вытекают из определения этой операции:
. Отметим основные свойства операции умножения вектора на число, которые непосредственно вытекают из определения этой операции: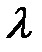 +
+ 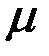 )а =
)а = 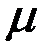 а.
а.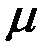 а) = (
а) = (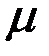 )а.
)а.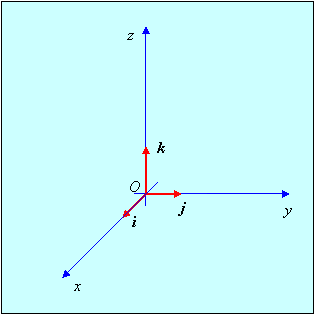 Пусть задан вектор а. Совместим его начальную точку с началом координат О, а через его конечную точку А проведем плоскости, перпендикулярные координатным осям. Пусть эти плоскости пересекают оси Ox, Oy, Oz в точках L, M, N соответственно.
Пусть задан вектор а. Совместим его начальную точку с началом координат О, а через его конечную точку А проведем плоскости, перпендикулярные координатным осям. Пусть эти плоскости пересекают оси Ox, Oy, Oz в точках L, M, N соответственно.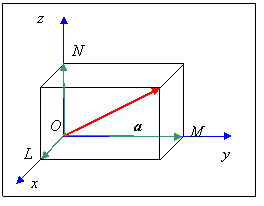 Нетрудно убедиться, что
Нетрудно убедиться, что 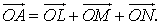 Поскольку вектора
Поскольку вектора 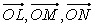 коллинеарны векторам i, j, k соответственно, то найдутся числа x1, y1, z1 такие, что
коллинеарны векторам i, j, k соответственно, то найдутся числа x1, y1, z1 такие, что 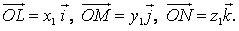 Следовательно, любой вектор а может быть представлен в виде a = x1i + y1j + z1k.
Следовательно, любой вектор а может быть представлен в виде a = x1i + y1j + z1k.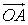 = (x1, y1, z1), будем писать А = { x1, y1, z1}.
= (x1, y1, z1), будем писать А = { x1, y1, z1}.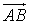 , если А = { x1, y1, z1} и
, если А = { x1, y1, z1} и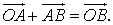 Отсюда
Отсюда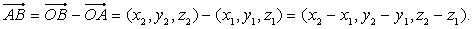
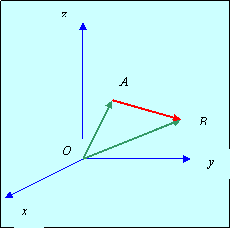 Прямую с заданным на ней направлением будем называть осью. Пусть дан вектор
Прямую с заданным на ней направлением будем называть осью. Пусть дан вектор 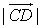 , если направление оси l совпадает с направлением вектора
, если направление оси l совпадает с направлением вектора 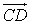 , и –
, и – 
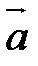 и
и 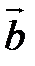 . Выберем в пространстве произвольную точку O и отложим от этой точки векторы
. Выберем в пространстве произвольную точку O и отложим от этой точки векторы 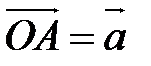 и
и 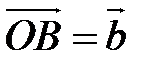 .
.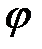
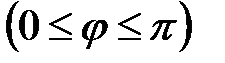 , на который нужно повернуть один из заданных векторов до его совпадения со вторым.
, на который нужно повернуть один из заданных векторов до его совпадения со вторым.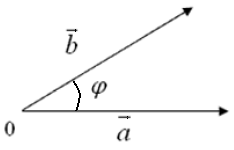
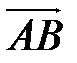 и ось
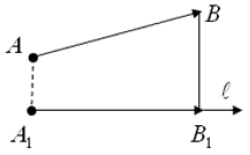
и ось 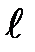 .
.
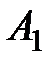 и
и 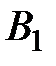 проекции на ось
проекции на ось 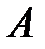 и B соответственно. Построим вектор
и B соответственно. Построим вектор 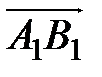 и назовем его компонентом вектора
и назовем его компонентом вектора 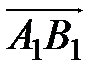 по этой оси, если компонента направлена в ту же сторону, что и ось
по этой оси, если компонента направлена в ту же сторону, что и ось 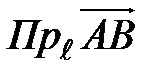 или
или 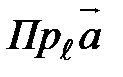 .
.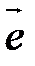 имеющий то же направление, что и ось
имеющий то же направление, что и ось 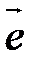 называется угол между вектором
называется угол между вектором 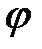 между вектором и осью:
между вектором и осью: 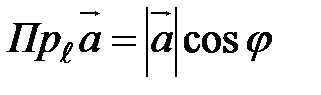 .
. 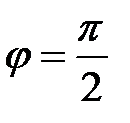 , то компонента есть нулевой вектор. Тогда и
, то компонента есть нулевой вектор. Тогда и 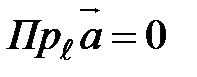 .
.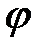
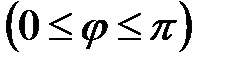
 . Опираясь на ранее рассмотренные линейные операции над векторами, можно убедиться, что для проекций векторов на ось справедливы следующие теоремы (без доказательств). Проекция суммы векторов на ось равна сумме проекции слагаемых векторов на ту же ось:
. Опираясь на ранее рассмотренные линейные операции над векторами, можно убедиться, что для проекций векторов на ось справедливы следующие теоремы (без доказательств). Проекция суммы векторов на ось равна сумме проекции слагаемых векторов на ту же ось: 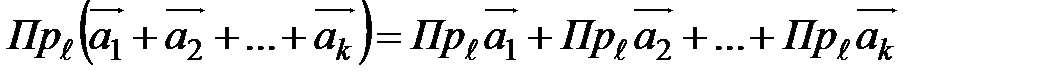 .
. 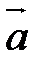 умножить на число
умножить на число 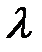 , то его проекция на ось умножится на это число:
, то его проекция на ось умножится на это число: 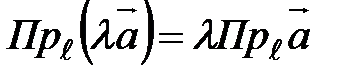 .
. 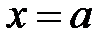 , (4.1)
, (4.1)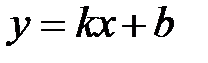 . (4.2)
. (4.2)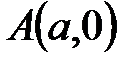 и параллельной оси
и параллельной оси 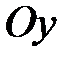 . Второе уравнение задает линейную функцию, графиком которой является невертикальная прямая. Напомним геометрический смысл параметров
. Второе уравнение задает линейную функцию, графиком которой является невертикальная прямая. Напомним геометрический смысл параметров 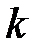 и
и 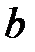 , входящих в уравнение (4.2).
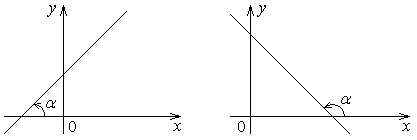
, входящих в уравнение (4.2).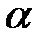 прямой
прямой 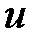 к оси
к оси 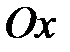 называется угол, откладываемый против часовой стрелки от положительного направления оси
называется угол, откладываемый против часовой стрелки от положительного направления оси 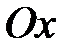 до прямой
до прямой 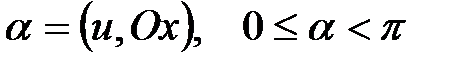 .
. 
 в уравнении (4.2), т.е.
в уравнении (4.2), т.е. 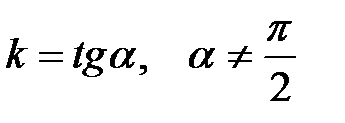 .
. 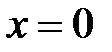 в уравнении (4.2), получим
в уравнении (4.2), получим 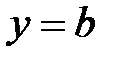 . Геометрически это означает, что число
. Геометрически это означает, что число 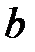 – ордината точки пересечения прямой с осью
– ордината точки пересечения прямой с осью 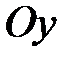 .
.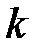 прямой
прямой 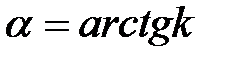 если
если 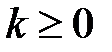 ,
, 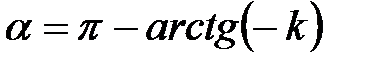 если
если 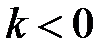 ,
, 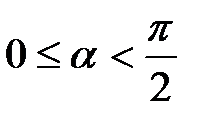 уравнение
уравнение 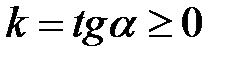 эквивалентно уравнению
эквивалентно уравнению 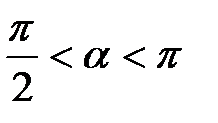 , то
, то 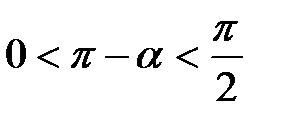 и, значит,
и, значит, 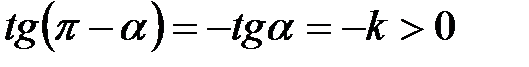 , откуда находим, что
, откуда находим, что 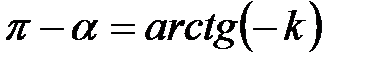 , или
, или 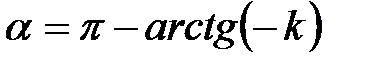 .
.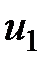 ,
, 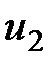 .
.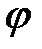 между прямыми
между прямыми 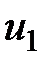 ,
, 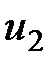 называется угол, на который нужно повернуть прямую
называется угол, на который нужно повернуть прямую 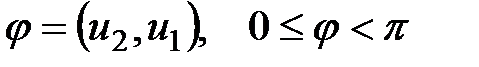 .
.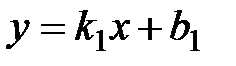 и
и 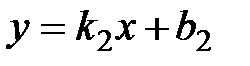 .
.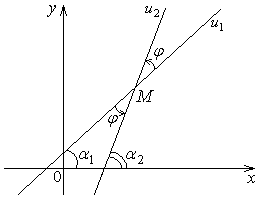 Обозначим через
Обозначим через 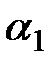 ,
,  углы наклона прямых
углы наклона прямых 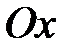 и заметим, что
и заметим, что 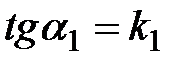 ,
, 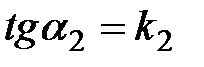 . Из определения угла между прямыми вытекает равенство
. Из определения угла между прямыми вытекает равенство 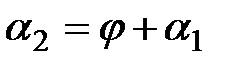 , откуда находим, что
, откуда находим, что 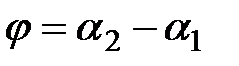 .
.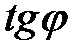 . В приложениях используется формула, выражающая
. В приложениях используется формула, выражающая 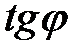 через угловые коэффициенты
через угловые коэффициенты 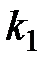 ,
, 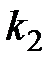 :
: 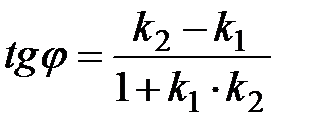 ,
, 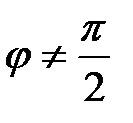 . (4.7)
. (4.7) 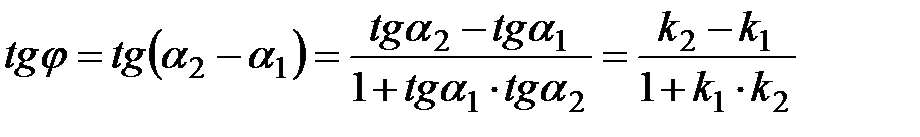 , что и требовалось.
, что и требовалось.


