
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Исследование функции при помощи производных
Возрастание и убывание функций Теорема 1. (необходимые условия). Если дифференцируемая на интервале (а;b) функция Теорема 2. (достаточные условия). Если функция Теоремы 1 и 2 позволяют довольно просто исследовать функцию на монотонность (функция, убывающая или возрастающая, называется монотонной). Пример. Исследовать функцию Решение:
-1 1
Ответ: даннаяфункция возрастает при Максимум и минимум функций Теорема (необходимое условие). Если дифференцируемая функция Теорема (достаточное условие экстремума). Если непрерывная функция Удобно использовать другой достаточный признак существования экстремума основанный на определении знака второй производной. Выпуклость графика функции. Точки перегиба Точка графика непрерывной функции Теорема. Если функция Если же Теорема (достаточное условие существования точек перегиба). Если вторая производная Общая схема исследования функции и построения Графика функции Исследование функции целесообразно вести в определенной последовательности. 1. Найти область определения функции. 2. Найти (если это можно) точки пересечения графика с осями координат. 3. Найти интервалы знакопостоянства функции (промежутки, на которых
4. Выяснить, является ли функция четной, нечетной или общего вида. 5. Найти асимптоты графика функции. 6. Найти интервалы монотонности функции. 7. Найти экстремумы функции. 8. Найти интервалы выпуклости и точки перегиба графика функции. Пример. Исследовать функцию 1. 2. Точка (0;0)- точка пересечения графика с осями ОХ и ОУ. 3. Функция знакоположительна (у>0) в интервалах 4. Функция 5. Прямые х = 1 и х = -1 являются ее вертикальными асимптотами. Выясним наличие наклонной асимптоты.
Следовательно, есть горизонтальная асимптота ее уравнение у=0. Наклонных асимптот нет. Прямая у=0 является асимптотой и при 6. Так как у’>0 в области определения, то функции является возрастающей на каждом интервале области определения. 7. Т.к. Данные точки не принадлежат области определения функции, значит, функция экстремумов не имеет. 8. Найдем Точка (0;0) – точка перегиба графика функции.
Практическая работа №3. «Исследование функции и построение графика» ТЕМА 4.
|
|||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 144; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.95.222 (0.008 с.) |
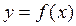 возрастает (убывает), то
возрастает (убывает), то 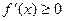
 для любого
для любого  .
.
 для любого
для любого  =x3-3x-4 на монотонность.
=x3-3x-4 на монотонность.


 Х
Х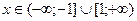 ,
, 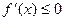 при
при 
 имеет экстремум в точке
имеет экстремум в точке 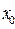 , то ее производная в этой точке равна нулю:
, то ее производная в этой точке равна нулю: 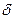 -окрестности критической точки
-окрестности критической точки 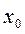 и при переходе через нее (слева на право) производная
и при переходе через нее (слева на право) производная 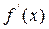 меняет знак с плюса на минус, то
меняет знак с плюса на минус, то 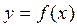 , отделяющая его части разной выпуклости, называется точкой перегиба.
, отделяющая его части разной выпуклости, называется точкой перегиба.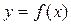 во всех точках интервала (a;b) имеет отрицательную вторую производную, т.е.
во всех точках интервала (a;b) имеет отрицательную вторую производную, т.е. 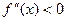 , то график функции в этом интервале выпуклый вверх.
, то график функции в этом интервале выпуклый вверх. для любого
для любого  при переходе через точку
при переходе через точку  в которой она равна нулю или не существует, меняет знак, то точка графика с абсциссой
в которой она равна нулю или не существует, меняет знак, то точка графика с абсциссой  есть точка перегиба.
есть точка перегиба.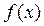 >0 или
>0 или 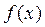 <0).
<0).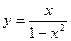 и построить ее график.
и построить ее график.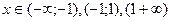

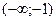 и
и 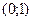 , знакоотрицательна – в
, знакоотрицательна – в  и
и 
 . Следовательно, график ее симметричен относительно начала координат. Для построения графика достаточно исследовать ее при
. Следовательно, график ее симметричен относительно начала координат. Для построения графика достаточно исследовать ее при  .
.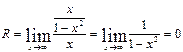
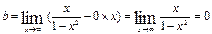
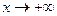 , и при
, и при  .
.
 .
.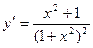 , то критическими точками является точки х1 = -1 и х2 = 1.
, то критическими точками является точки х1 = -1 и х2 = 1.
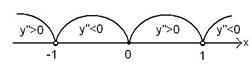
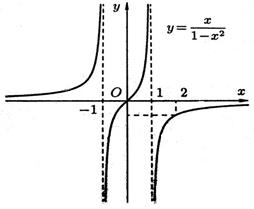 График выпуклый вверх на интервалах
График выпуклый вверх на интервалах 


