
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Производная функции, геометрический смысл производной. Исследование функции с помощью производной и построение графикаСтр 1 из 7Следующая ⇒
Математика ЛЕКЦИИ 2 курс. ТЕМА 1 Определение: Пусть функция f (x) определена в некоторой окрестности точки а, кроме, быть может, самой точки а. Число А называется пределом функции f (x) в точке а (или при х, стремящемся к а), если для любых значений аргумента (х ¹ а) изсколь угодно малой окрестности точки а, последовательность соответствующих значений функции f (x) мало чемотличается от А (т.е. f (x) приближенно равны А). В этом случае пишут Свойства пределов: Теорема 1: Функция не может иметь двух разных пределов в точке. Теорема 2: Предел суммы (разности) функций равен сумме (разности) их пределов, если последние существуют: Теорема 3: Предел произведения функций равен произведению их пределов, если последние существуют: Следствие: Постоянный множитель можно выносить за знак предела, т.е. Теорема 4: Предел отношений двух функций равен отношению их пределов, если последние существуют и предел делителя отличен от нуля: 2. Примеры: 1) Предел многочлена. Пример. Вычислить Решение:
Таким образом, для вычисления предела многочлена f (x) при x → x 0 достаточно вместо переменной x подставить значение x 0, к которому она стремится, и выполнить соответствующие действия, т.е. 2) Предел отношения двух многочленов, Если g (x 0) ≠ 0, то можно применить теорему о пределе частного. Пример. Пусть требуется вычислить Решение: Здесь f (x) = x 3 – 2 x – 3 и g (x) = x 2 + 3 x + 3. Т.к g (3) = 32 + 3 ∙ 3 + 3 = 21 ≠ 0. то имеем: Пример. Вычислить Решение: здесь ƒ (2) = 22 - 5∙2 + 6 = 0, g (2) = 22 - 6∙2 + 8 = 0. Так как x ≠ 2, имеем
44) Предел функции на бесконечности Пример 1. Вычислить Решение:
Пример 2. Вычислить
Пример 3. Вычислить Решение: Практическая работа №1«Вычисление пределов функции».
ТЕМА 2 Понятие производной функции. Определение: Пусть функция ƒ (x) определена в некоторой окрестности точки x 0. Производной функции ƒ (x) в точке x 0 называется отношение приращения функции ∆ƒ (x 0) к приращению аргумента ∆ x при ∆ x → 0, если этот предел существует, и обозначается ƒ ’ (x 0). Итак,
Производную функции y = ƒ (x), x є (a; b) в точке x обозначают ƒ ’ (x), y ’ (x), Операция нахождения производной называется дифференцированием функции. Функция, имеющая производную в точке x 0, называется дифференцируемой в этой точке. Функция, имеющая производную в каждой точке интервала (a; b), называется дифференцируемой на этом интервале; при этом производную ƒ ’ (x) можно рассматривать как функцию на (a; b). Правила дифференцирования 1) 2) где u и υ - дифференцируемые функции переменной x, C - константа. Правило дифференцирования сложной функции Пусть дана сложная функция Таблица производных основных элементарных функций
Пример 1. Вычислить производные сложных функций а) Решение: а)
б)
Практическая работа №2 «Нахождение производной функции» ТЕМА 3 Максимум и минимум функций Теорема (необходимое условие). Если дифференцируемая функция Теорема (достаточное условие экстремума). Если непрерывная функция Удобно использовать другой достаточный признак существования экстремума основанный на определении знака второй производной. Графика функции Исследование функции целесообразно вести в определенной последовательности. 1. Найти область определения функции. 2. Найти (если это можно) точки пересечения графика с осями координат.
3. Найти интервалы знакопостоянства функции (промежутки, на которых 4. Выяснить, является ли функция четной, нечетной или общего вида. 5. Найти асимптоты графика функции. 6. Найти интервалы монотонности функции. 7. Найти экстремумы функции. 8. Найти интервалы выпуклости и точки перегиба графика функции. Пример. Исследовать функцию 1. 2. Точка (0;0)- точка пересечения графика с осями ОХ и ОУ. 3. Функция знакоположительна (у>0) в интервалах 4. Функция 5. Прямые х = 1 и х = -1 являются ее вертикальными асимптотами. Выясним наличие наклонной асимптоты.
Следовательно, есть горизонтальная асимптота ее уравнение у=0. Наклонных асимптот нет. Прямая у=0 является асимптотой и при 6. Так как у’>0 в области определения, то функции является возрастающей на каждом интервале области определения. 7. Т.к. Данные точки не принадлежат области определения функции, значит, функция экстремумов не имеет. 8. Найдем Точка (0;0) – точка перегиба графика функции.
Практическая работа №3. «Исследование функции и построение графика» ТЕМА 4. Таблица неопределенных интегралов.
2.Примеры: 1) Решение: 1) 2)
Практическая работа №4. «Неопределенный интеграл» ТЕМА 5 ТЕМА 9 Задачи, приводящие к дифференциальным уравнениям. Задача Коши. Дифференциальные уравнения с разделяющимися переменными. Общие и частные решения. Однородные дифференциальные уравнения первого порядка. Линейные однородные уравнения второго порядка с постоянными коэффициентами Обыкновенным дифференциальным уравнением 1 -го порядка называется выражение вида Решением дифференциального уравнения называется такая функция у=у(х), которая при подстановке ее в это уравнение обращает его в верное тождество. Общим решением дифференциального уравнения 1-го порядка называется такое его решение
где числа Решение уравнения , удовлетворяющее начальному условию (4), называется решением задачи Коши и записывается в виде
Решить задачу Коши (5) означает найти интегральную кривую дифференциального уравнения, которая проходит через заданную точку Примеры. Пример№1: Решить дифференциальные уравнения: а) Решение: а) Приведём уравнение к виду Интегрируем обе части уравнения: Ответ: б) Приведём уравнение к виду: разделим обе части уравнения на Переменные разделены. Интегрируем обе части уравнения:
Применим основное логарифмическое тождество получим
При делении на Ответ: Пример №2: Найдите решения задачи Коши: а) Решение: а)
Интегрируем обе части уравнения:
Подставим начальное условие в общее решение, получим
Так как по условию Ответ: б)
Интегрируем обе части уравнения:
Так как по условию Ответ:
Решите следующие задачи. 1. Решите дифференциальные уравнения: а) г) 2. Найдите решения задачи Коши: а) б)
Дифференциальное уравнение второго порядка, содержит: Решить дифференциальное уравнение – это значит, найти множество функций 2.Однородное ДУ второго порядка с постоянными коэффициентами имеет следующий вид:
Для того чтобы решить данное ДУ, нужно составить так называемое характеристическое уравнение:
По какому принципу составлено характеристическое уравнение, отчётливо видно:
Существуют три варианта развития событий. Если характеристическое уравнение
Пример. Решить дифференциальное уравнение Решение: составим и решим характеристическое уравнение:
Ответ: общее решение: Основные понятия комбинаторики В разделе математики, который называется комбинаторикой, решаются некоторые задачи, связанные с рассмотрением множеств и составлением различных комбинаций из элементов этих множеств. Например, если взять 10 различных цифр 0, 1, 2, 3,…, 9 и составлять из них комбинации, то будем получать различные числа, например 143, 431, 5671, 1207, 43 и т.п. Мы видим, что некоторые из таких комбинаций отличаются только порядком цифр (например, 143 и 431), другие - входящими в них цифрами (например, 5671 и 1207), третьи различаются и числом цифр (например, 143 и 43). Таким образом, полученные комбинации удовлетворяют различным условиям. В зависимости от правил составления можно выделить три типа комбинаций: перестановки, размещения, сочетания. Предварительно познакомимся с понятием факториала. Произведение всех натуральных чисел от 1 до n включительно называют n -факториалом и пишут
Пример 1. Вычислить: а) Решение. а) б) Так как Тогда получим
в)
Перестановки. Комбинация из n элементов, которые отличаются друг от друга только порядком элементов, называются перестановками. Перестановки обозначаются символом Р n, где n- число элементов, входящих в каждую перестановку. (Р - первая буква французского слова permutation - перестановка). Число перестановок можно вычислить по формуле
или с помощью факториала:
Запомним, что 0!=1 и 1!=1. Пример 2. Сколькими способами можно расставлять на одной полке шесть различных книг? Решение. Искомое число способов равно числу перестановок из 6 элементов, т.е.
2. Размещения. Размещениями из m элементов в n в каждом называются такие соединения, которые отличаются друг от друга либо самими элементами (хотя бы одним), либо порядком из расположения. Размещения обозначаются символом При этом полагают, что n Число размещений можно вычислить по формуле
т.е. число всех возможных размещений из m элементов по n равно произведению n последовательных целых чисел, из которых большее есть m.
Запишем эту формулу в факториальной форме:
Пример 3. Сколько вариантов распределения трех путевок в санатории различного профиля можно составить для пяти претендентов? Решение. Искомое число вариантов равно числу размещений из 5 элементов по 3 элемента, т.е.
Сочетания. Сочетаниями называются все возможные комбинации из m элементов по n, которые отличаются друг от друга по крайней мере хотя бы одним элементом (здесь m и n -натуральные числа, причем n Число сочетаний из m элементов по n обозначаются В общем случае число из m элементов по n равно числу размещений из m элементов по n, деленному на число перестановок из n элементов:
Используя для чисел размещений и перестановок факториальные формулы, получим:
Пример 4. В бригаде из 25 человек нужно выделить четырех для работы на определенном участке. Сколькими способами это можно сделать? Решение. Так как порядок выбранных четырех человек не имеет значения, то это можно сделать Находим по первой формуле
Кроме того, при решении задач используются следующие формулы, выражающие основные свойства сочетаний:
(по определению полагают
Решение комбинаторных задач Задача 1. На факультете изучается 16 предметов. На понедельник нужно в расписание поставить 3 предмета. Сколькими способами можно это сделать? Решение. Способов постановки в расписание трех предметов из 16 столько, сколько можно составить размещений из 16 элементов по 3.
Задача 2. Из 15 объектов нужно отобрать 10 объектов. Сколькими способами это можно сделать? Решение.
Задача 3. В соревнованиях участвовало четыре команды. Сколько вариантов распределения мест между ними возможно? Решение.
Задача 4. Сколькими способами можно составить дозор из трех солдат и одного офицера, если имеется 80 солдат и 3 офицера? Решение. Солдат в дозор можно выбрать
способами, а офицеров Задача 5. Найти Решение. Так как
По определению сочетания следует, что Ответ: 9 Дискретная и непрерывная случайные величины.Закон распределения случайной величины Нахождение математического ожидания. Дисперсия и среднеквадратичное отклонение дискретной случайной величины, заданной законом распределения Случайная величина, способы ее задания Случайной называется величина, которая в результате испытания может принять то или иное числовое значение, причем заранее неизвестно, какое именно. Если для какой- либо величины ее измерение повторять многократно в практически одинаковых условиях, то обнаружится, что всякий раз получаются несколько отличные друг от друга результаты. Это складывается влияние причин двух видов: 1) основных, определяющих главное значение результата; 2) второстепенных, обуславливающих их расхождение. При совместном действии этих причин понятия необходимости и случайности оказываются тесно связанными между собой, но необходимое преобладает над случайным. Таким образом, возможные значения случайных величин принадлежат некоторым числовым множествам. Случайным является то, что на этих множествах величины могут принять любое значение, но какое именно, заранее сказать нельзя. Случайная величина связана со случайным событием. Если случайное событие - качественная характеристика испытаний, то случайная величина - его количественная характеристика. Случайные величины обозначают заглавными латинскими буквами Вероятность того, что случайная величина
Случайные величины задают законами распределения. Закон распределения случайной величины - это соответствие, установленное между возможными значениями случайной величины и их вероятностями. Законы распределения могут быть заданы тремя способами: табличным, графическим, аналитическим. Способ задания зависит от типа случайной величины. Различают два основных типа случайных величин: дискретные и непрерывно распределенные случайные величины. Математика ЛЕКЦИИ 2 курс. ТЕМА 1 Определение: Пусть функция f (x) определена в некоторой окрестности точки а, кроме, быть может, самой точки а. Число А называется пределом функции f (x) в точке а (или при х, стремящемся к а), если для любых значений аргумента (х ¹ а) изсколь угодно малой окрестности точки а, последовательность соответствующих значений функции f (x) мало чемотличается от А (т.е. f (x) приближенно равны А). В этом случае пишут Свойства пределов: Теорема 1: Функция не может иметь двух разных пределов в точке. Теорема 2: Предел суммы (разности) функций равен сумме (разности) их пределов, если последние существуют: Теорема 3: Предел произведения функций равен произведению их пределов, если последние существуют: Следствие: Постоянный множитель можно выносить за знак предела, т.е. Теорема 4: Предел отношений двух функций равен отношению их пределов, если последние существуют и предел делителя отличен от нуля: 2. Примеры: 1) Предел многочлена. Пример. Вычислить Решение:
Таким образом, для вычисления предела многочлена f (x) при x → x 0 достаточно вместо переменной x подставить значение x 0, к которому она стремится, и выполнить соответствующие действия, т.е. 2) Предел отношения двух многочленов, Если g (x 0) ≠ 0, то можно применить теорему о пределе частного. Пример. Пусть требуется вычислить Решение: Здесь f (x) = x 3 – 2 x – 3 и g (x) = x 2 + 3 x + 3. Т.к g (3) = 32 + 3 ∙ 3 + 3 = 21 ≠ 0. то имеем: Пример. Вычислить Решение: здесь ƒ (2) = 22 - 5∙2 + 6 = 0, g (2) = 22 - 6∙2 + 8 = 0. Так как x ≠ 2, имеем
44) Предел функции на бесконечности Пример 1. Вычислить Решение:
Пример 2. Вычислить
Пример 3. Вычислить Решение: Практическая работа №1«Вычисление пределов функции».
|
|||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 121; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.126.39 (0.242 с.) |
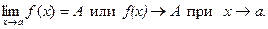
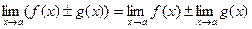 ,
,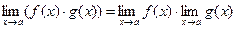 ,
, ,
,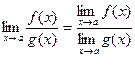 ,
,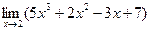
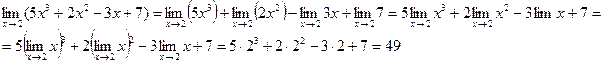
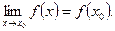
 , где x 0 – число.
, где x 0 – число.
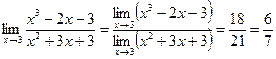
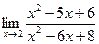 .
.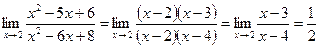 .
.  .
.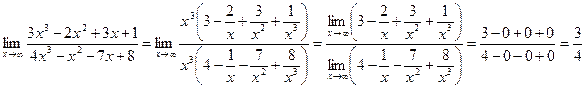 .
.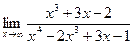 .
.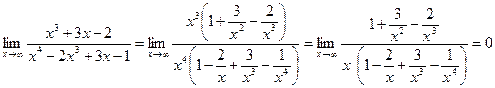 .
.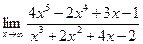 .
.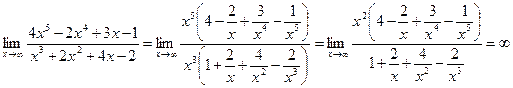
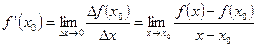 (1)
(1) ,
,  , причём все эти обозначения равноправны.
, причём все эти обозначения равноправны.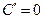 3)
3) 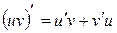 ,
, 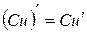 ;
; 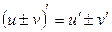 , 4)
, 4) 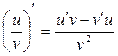 ,
,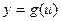 , где
, где 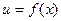 . Если функция
. Если функция 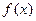 и дифференцируема в точке
и дифференцируема в точке 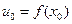 , то сложная функция
, то сложная функция 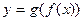 в данной точке х 0 имеет производную, которая находится по формуле
в данной точке х 0 имеет производную, которая находится по формуле 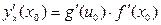 или
или 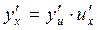

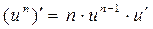
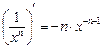
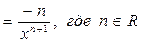
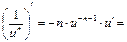


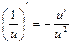

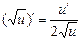
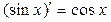

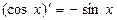
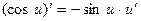
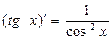

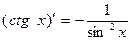
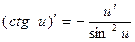
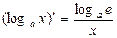
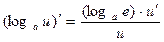

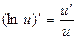
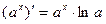 ,
, 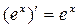
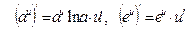
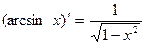
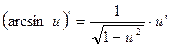
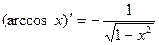
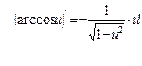
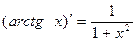
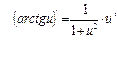
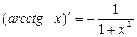
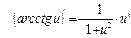
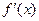 , если
, если 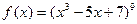 , б)
, б) 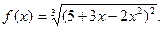 ,
,
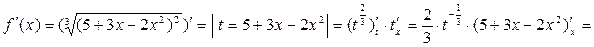
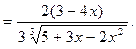
 имеет экстремум в точке
имеет экстремум в точке 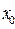 , то ее производная в этой точке равна нулю:
, то ее производная в этой точке равна нулю:  =0.
=0.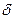 -окрестности критической точки
-окрестности критической точки 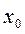 и при переходе через нее (слева на право) производная
и при переходе через нее (слева на право) производная 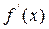 меняет знак с плюса на минус, то
меняет знак с плюса на минус, то 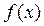 >0 или
>0 или 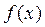 <0).
<0).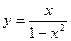 и построить ее график.
и построить ее график.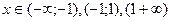

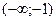 и
и 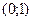 , знакоотрицательна – в
, знакоотрицательна – в  и
и 
 . Следовательно, график ее симметричен относительно начала координат. Для построения графика достаточно исследовать ее при
. Следовательно, график ее симметричен относительно начала координат. Для построения графика достаточно исследовать ее при  .
.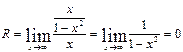
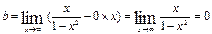
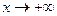 , и при
, и при  .
.
 .
.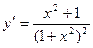 , то критическими точками является точки х1 = -1 и х2 = 1.
, то критическими точками является точки х1 = -1 и х2 = 1.
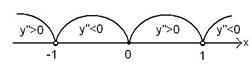
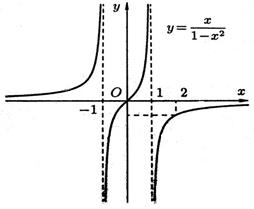 График выпуклый вверх на интервалах
График выпуклый вверх на интервалах 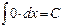 , где C – константа.
2.
, где C – константа.
2. 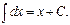 3.
3. 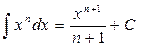 , n¹–1.
4.
, n¹–1.
4. 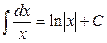 .
5.
.
5. 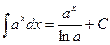 ,
,  .
6.
.
6. 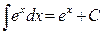 .
7.
.
7. 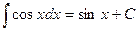 .
.
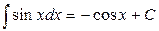
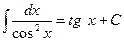 .
9.
.
9.  .
10.
.
10. 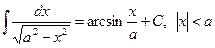 .
11.
.
11.  .
12.
.
12. 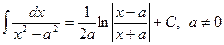 .
13.
.
13. 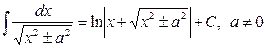 .
В случае
.
В случае  , предполагается что,
, предполагается что, 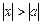 .
.
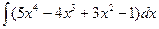 ; 2)
; 2) 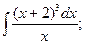
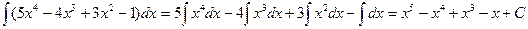 ;
;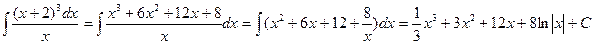
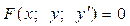 , т.е. уравнение, содержащее неизвестную, искомую функцию y=y(x) и ее производную.
, т.е. уравнение, содержащее неизвестную, искомую функцию y=y(x) и ее производную.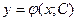 , которое является функцией переменной х и произвольной независимой постоянной С. (Независимость постоянных означает отсутствие каких-либо соотношений между ними).
, которое является функцией переменной х и произвольной независимой постоянной С. (Независимость постоянных означает отсутствие каких-либо соотношений между ними).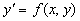 Определение: Задача нахождения решения уравнения , удовлетворяющего
Определение: Задача нахождения решения уравнения , удовлетворяющего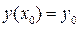 условию (4)
условию (4) 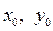 – заданные числа, называется задачей Коши. Условие (4) называется начальным условием.
– заданные числа, называется задачей Коши. Условие (4) называется начальным условием.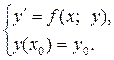 . (5)
. (5)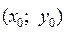 .
.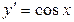 ; б)
; б) 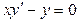 .
.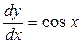 ;
; 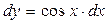 .
.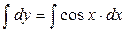 ;
; 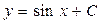 .
. .
. ;
; 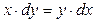 .
. :
:  .
.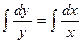 ;
; 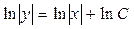 .
.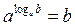 или
или  ,
,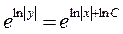 или
или  .
.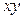 могли быть потеряны решения
могли быть потеряны решения 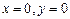 . Очевидно, что
. Очевидно, что 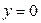 является решением данного уравнения при C=0, а
является решением данного уравнения при C=0, а  – нет. Таким образом, формула
– нет. Таким образом, формула  , где С – произвольная постоянная, задаёт все решения данного уравнения.
, где С – произвольная постоянная, задаёт все решения данного уравнения. .
. 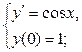 б)
б) 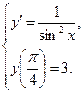
 Найдём общее решение дифференциального уравнения.
Найдём общее решение дифференциального уравнения.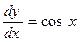 ;
; 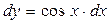 .
.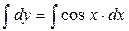 ;
; 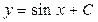 .
.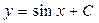 – общее решение дифференциального уравнения.
– общее решение дифференциального уравнения.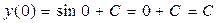 .
. , то С=1. Тогда частное решение данного дифференциального уравнения имеет вид
, то С=1. Тогда частное решение данного дифференциального уравнения имеет вид 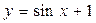 .
.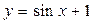 .
.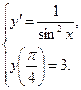 Найдём общее и частное решение дифференциального уравнения.
Найдём общее и частное решение дифференциального уравнения.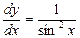 ;
; 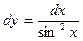 .
. ;
; 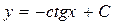 .
.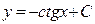 – общее решение дифференциального уравнения. Подставим начальное условие в общее решение, получим
– общее решение дифференциального уравнения. Подставим начальное условие в общее решение, получим  .
. , то –1+С=3, С=4. Тогда частное решение данного дифференциального уравнения имеет вид
, то –1+С=3, С=4. Тогда частное решение данного дифференциального уравнения имеет вид  .
. .
.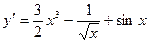 ; б)
; б) 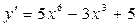 ; в)
; в) 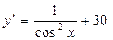 ;
;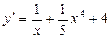 ; д)
; д) 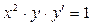 ; е)
; е)  .
. в)
в)  д)
д) 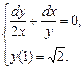
 г)
г) 
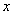 ;
;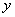 (функцию);
(функцию);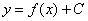 , которые удовлетворяют данному уравнению. Такое множество функций называется общим решением дифференциального уравнения.
, которые удовлетворяют данному уравнению. Такое множество функций называется общим решением дифференциального уравнения. , где
, где  и
и 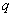 – константы (числа), а в правой части – строго ноль.
– константы (числа), а в правой части – строго ноль.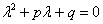
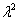 ;
;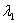 ,
,  (т.е., если дискриминант
(т.е., если дискриминант 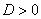 ), то общее решение однородного уравнения выглядит так:
), то общее решение однородного уравнения выглядит так: , где
, где 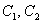 – константы.
– константы.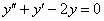

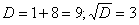
 ,
, 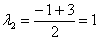
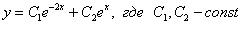
 .
.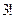 ; б)
; б) 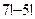 ; в)
; в) 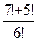 .
.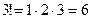 .
.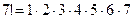 и
и 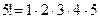 , то можно вынести за скобки
, то можно вынести за скобки 
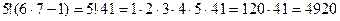 .
.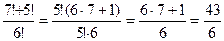 .
.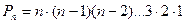
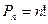
 .
. , где m - число всех имеющихся элементов, n - число элементов в каждой комбинации. (А- первая буква французского слова arrangement, что означает «размещение, приведение в порядок»).
, где m - число всех имеющихся элементов, n - число элементов в каждой комбинации. (А- первая буква французского слова arrangement, что означает «размещение, приведение в порядок»).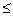 m.
m.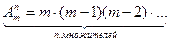 ,
,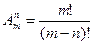 .
.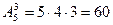 .
.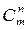 (С -первая буква французского слова combination - сочетание).
(С -первая буква французского слова combination - сочетание).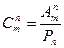
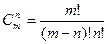
 способами.
способами.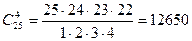 .
.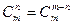
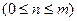
 и
и 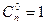 );
);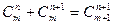 .
.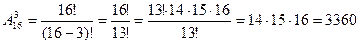 .
.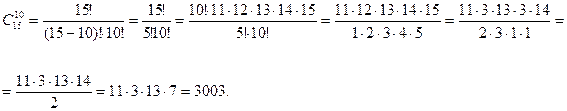
 .
.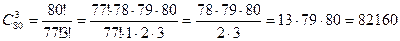
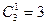 способами. Так как с каждой командой из солдат может пойти любой офицер, то всего имеется
способами. Так как с каждой командой из солдат может пойти любой офицер, то всего имеется 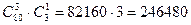 способов.
способов. , если известно, что
, если известно, что  .
.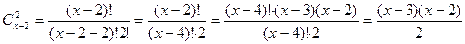 , то получим
, то получим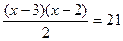 ,
,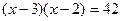 ,
,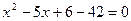 ,
,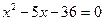
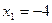 ,
, 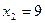 .
.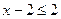 ,
, 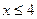 . Т.о.
. Т.о. 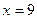 .
.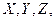 а их значение – прописными-
а их значение – прописными- 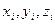 .
.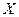 примет значение
примет значение 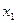 обозначают:
обозначают: и т.д.
и т.д.


