
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие линейного отображения
Всюду определенная функция
Нулевое отображение - отображение Тождественное отображение - отображение Проектирование пространства V на подпространство U параллельно пространству W: пусть векторное пространство V является прямой суммой подпространств U и W. Каждый вектор y + z, где x1 + x2 = (y1 + y2) + (z1 + z2),
Ядро и образ линейного отображения
Пусть Обозначим W множество тех элементов z из V2, для которых найдется элемент x такой, что
Дефект ядра - размерность ядра линейного отображения. Ранг образа - размерность образа линейного отображения.
Матрица линейного отображения
Пусть V1 и V2 - конечномерные векторные пространства над полем F, ● a1, a2,..., am - базис пространства V1, в частности, dim V1 = m; ● b1, b2, …, bn - базис пространства V2, в частности, dim V2 = n. Пусть x - произвольный вектор из V1. Распишем его через базис пространства V1: ● x = x1a1 + x2a2 + … + xmam. Тогда Вывод: образы базисных векторов пространства V1 являются системой образующих для образа отображения
Выразим образ
Запишем координаты вектора в виде столбца:
Вся информация, которая нам нужна про
Матрица линейного отображения - таблица, составленная из координат образов базисных векторов, полученных при линейном отображении
[ При фиксированных базисах пространств V1 и V2 получаем отображение φ:
|
|||||||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 107; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.37.68 (0.01 с.) |
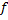 : V1 ⟶ V2 называется линейным отображением, если
: V1 ⟶ V2 называется линейным отображением, если  .
.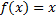 .
. однозначно представим в виде суммы
однозначно представим в виде суммы и
и  . Положим
. Положим 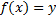 . Пусть x1 = y1 + z1, x2 = y2 + z2. Поскольку
. Пусть x1 = y1 + z1, x2 = y2 + z2. Поскольку .
.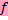 - Ker
- Ker  .
.

 ].
].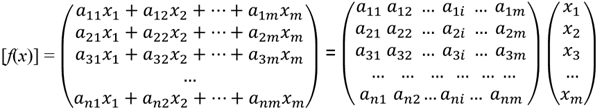
 ⟶ [
⟶ [ 


