
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Базис векторного пространства
Система векторов Σ векторного пространства V называется системой образующих этого пространства, если любой вектор из V линейно выражается через какие-то вектора из системы Σ.
Базис векторного пространства - линейно независимая система образующих. Базис плоскости - произвольная пара неколлинеарных векторов, лежащих в этой плоскости. Базис обычного трехмерного пространства - произвольная тройка некомпланарных векторов этого пространства. Стандартный базис пространства
Размерность пространства - число векторов в базисе (если у векторного пространства есть конечный базис) - dim V.
Векторные пространства V1 и V2 над одним и тем же полем F изоморфны, если существует биекция f из V1 и V2 (называемая изоморфизмом) такая, что f сохраняет операции, т.е. ∀x1, x2 ∈ V1 ∀t ∈ F f(x1 + x2) = f(x1) + f(x2) и f(tx) = t * f(x).
-----------Подпространства-----------
Непустое подмножество M векторного пространства V над полем F называется подпространством пространства V, если выполняются следующие условия: 1) если x, y ∈ M, то x + y ∈ M (замкнутость подпространства относительно сложения векторов); 2) если x ∈ M, а t ∈ F, то tx ∈ M (замкнутость подпространства относительно умножения вектора на скаляр).
Пусть V — произвольное векторное пространство и a1, a2,..., ak ∈ V. Обозначим через M множество всевозможных линейных комбинаций векторов a1, a2,..., ak. Пусть x, y ∈ M, т. е. x = s1a1 + s2a2 + · · · + skak и y = t1a1 + t2a2 + · · · + tkak для некоторых скаляров s1,s2,...,sk и t1,t2,...,tk. Пусть, далее, t — произвольный скаляр. Тогда x + y = (s1a1 + s2a2 + · · · + skak) + (t1a1 + t2a2 + · · · + tkak) = (s1 + t1)a1 + (s2 + t2)a2 + · · · + (sk + tk)ak и tx = t(s1a1 + s2a2 + · · · + skak) = (ts1)a1 + (ts2)a2 + · · · + (tsk)ak. Мы видим, что x + y,tx ∈ M, т. е. M — подпространство пространства V. Оно называется подпространством, порожденным векторами a1, a2,..., ak, или линейной оболочкой векторов a1, a2,..., ak - 〈a1, a2,..., ak〉.
|
||||||||||||||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 114; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.218.230 (0.004 с.) |
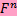 - система векторов e1, e2,..., en.
- система векторов e1, e2,..., en.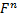 .
.



