Скалярное произведение векторов
Прямая называется осью, если на ней зафиксирован ненулевой вектор, называемый направляющим вектором этой оси.
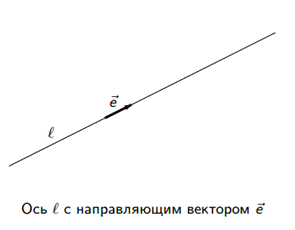
Пусть  — вектор. Его проекцией на ось ℓ называется число, обозначаемое пр
— вектор. Его проекцией на ось ℓ называется число, обозначаемое пр 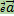 и определяемое следующим образом:
и определяемое следующим образом:
● если  ⊥ ℓ, то пр
⊥ ℓ, то пр 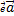 := 0.
:= 0.
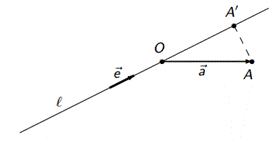
● иначе - отложим вектор  от какой-нибудь точки O прямой ℓ.
от какой-нибудь точки O прямой ℓ.
Тогда пр 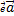 :=
:=
○ | 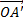 |, если
|, если 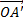 ⇈
⇈ 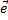
○ −| 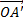 |, если
|, если 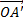 ↑↓
↑↓ 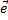
Свойства проекций:
Если ℓ — ось с направляющим вектором 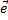 , ,  и и  — произвольные вектора, а t — произвольное число, то:
1) пр — произвольные вектора, а t — произвольное число, то:
1) пр 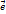 ( ( + +  ) = пр ) = пр 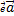 + пр + пр 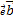 ;
2) пр ;
2) пр 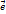 (t (t  ) = t пр ) = t пр 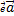 . .
|
Угол между осью ℓ и вектором 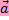 — угол между направляющим вектором оси и
— угол между направляющим вектором оси и  .
.
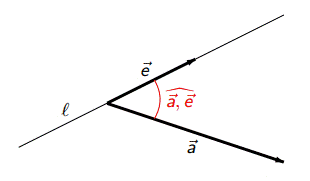
пр 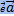 = |
= | 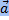 | cos(
| cos(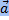 ,
, 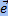 )
)
Скалярным произведением ненулевых векторов называется число, равное произведению длин этих векторов на косинус угла между ними - 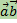 .
.
Скалярное произведение нулевого вектора на любой вектор по определению равно 0.
cos(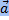 ,
, 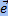 ) =
) = 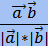
Если вектора  и
и  — ненулевые, то
— ненулевые, то
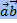 = |
= | 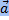 | · |
| · | 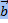 | · cos(
| · cos(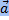 ,
, 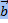 ) = |
) = | 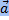 | · пр
| · пр 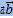 = |
= | 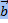 | · пр
| · пр 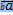
Скалярный квадрат вектора 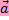 - скалярное произведение вектора
- скалярное произведение вектора  на себя -
на себя - 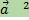 .
.
| Скалярный квадрат вектора равен квадрату его длины.
|
Ненулевые вектора  и
и  называются ортогональными, если они лежат на перпендикулярных прямых -
называются ортогональными, если они лежат на перпендикулярных прямых - 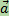 ⊥
⊥ 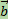 .
.
Нулевой вектор по определению считается ортогональным любому вектору.
Векторы  и и  ортогональны тогда и только тогда, когда ортогональны тогда и только тогда, когда 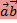 = 0. = 0.
|
Замечание об острых и тупых углах:
Угол между ненулевыми векторами  и и  является:
а) острым тогда и только тогда, когда является:
а) острым тогда и только тогда, когда 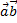 > 0;
б) прямым тогда и только тогда, когда > 0;
б) прямым тогда и только тогда, когда 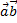 = 0;
в) тупым тогда и только тогда, когда = 0;
в) тупым тогда и только тогда, когда 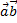 < 0. < 0.
|
Свойства скалярного произведения:
Если  , ,  , , 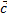 — произвольные вектора, а t — произвольное число, то:
1) — произвольные вектора, а t — произвольное число, то:
1) 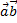 = = 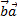 (скалярное произведение коммутативно);
2) ( (скалярное произведение коммутативно);
2) ( + +  ) ) 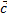 = = 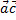 + + 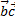 (скалярное произведение дистрибутивно относительно сложения векторов);
3) (t (скалярное произведение дистрибутивно относительно сложения векторов);
3) (t  ) )  = t( = t(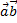 );
4) );
4) 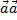 ≥ 0, причем ≥ 0, причем 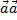 = 0 тогда и только тогда, когда = 0 тогда и только тогда, когда  = = 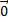 . .
|
Если вектора  и и  таковы, что для любого вектора таковы, что для любого вектора 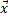 выполняется равенство выполняется равенство 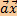 = = 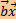 , то , то 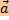 = = 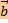 . .
|
Базис называется ортогональным, если его вектора попарно ортогональны. Ортогональный базис называется ортонормированным, если длины всех базисных векторов равны единице.
Метод Крамера
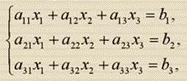
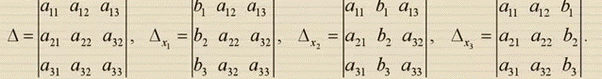
Если определитель системы не равен 0, то рассматриваемая система имеет только одно решение, причем
-----------------Плоскость-----------------
| Пусть в пространстве задана произвольная система координат. Тогда всякая плоскость может быть задана некоторым уравнением вида
Ax + By + Cz + D = 0,
в котором по крайней мере один из коэффициентов A, B, C отличен от 0.
Обратно, любое уравнение
Ax + By + Cz + D = 0,
в котором по крайней мере один из коэффициентов A, B, C отличен от 0, задает некоторую плоскость.
|
Направляющий вектор плоскости - любой ненулевой вектор, коллинеарный данной плоскости.
x = x0 + q1u + q2v
y = y0 + r1u + r2v - параметрические уравнения плоскости.
z = z0 + s1u + s2v
| x - x0
| y - y0
| z - z0
|
|
| q1
| r1
| s1
| = 0 - каноническое уравнение плоскости.
|
| q2
| r2
| s2
|
|
Пусть плоскость задана уравнением Ax + By + Cz + D = 0. Положим 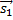 = (−B, A, 0), = (−B, A, 0), 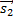 = (−C, 0, A) и = (−C, 0, A) и 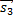 = (0, −C,B). Тогда по крайней мере два из векторов = (0, −C,B). Тогда по крайней мере два из векторов 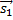 , , 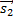 и и 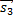 не коллинеарны и являются направляющими векторами плоскости (если A не коллинеарны и являются направляющими векторами плоскости (если A 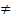 0, то этими свойствами обладают вектора 0, то этими свойствами обладают вектора 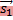 и и 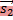 , если B , если B 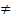 0 — вектора 0 — вектора 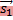 и и 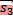 , а если C , а если C 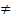 0 — вектора 0 — вектора 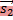 и и 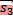 ). ).
|
Пусть плоскость π задана уравнением Ax + By + Cz + D = 0. Тогда вектор 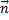 = (A,B,C) называется главным вектором плоскости π.
= (A,B,C) называется главным вектором плоскости π.
| Главный вектор плоскости не коллинеарен этой плоскости.
|
| Если система координат является прямоугольной декартовой, то главный вектор плоскости является ее нормальным вектором. Другими словами, если плоскость задана в прямоугольной декартовой системе координат уравнением Ax + By + Cz + D = 0, то вектор с координатами (A,B,C) перпендикулярен этой плоскости.
|
| x - x0
| y - y0
| z - z0
|
|
| x1 - x0
| y1 - y0
| z1 - z0
| = 0 - уравнение плоскости по 3 точкам.
|
| x2 - x0
| y2 - y0
| z2 - z0
|
|
Пусть плоскость σ1 задана уравнением A1x + B1y + C1z + D1 = 0, а плоскость σ2 — уравнением A2x + B2y + C2z + D2 = 0. Плоскости σ1 и σ2:
1) пересекаются тогда и только тогда, когда 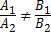 или или 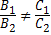 ;
2) параллельны тогда и только тогда, когда ;
2) параллельны тогда и только тогда, когда 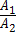 = = 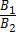 = = 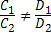 ;
3) совпадают тогда и только тогда, когда ;
3) совпадают тогда и только тогда, когда 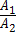 = = 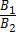 = = 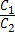 = = 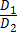 . .
|
Пусть плоскость σ задана уравнением Ax + By + Cz + D = 0. Все пространство делится этой плоскостью на три непересекающиеся части: саму плоскость σ и два полупространства.
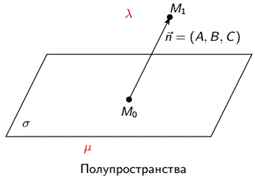
| Пусть M(x′, y′, z′) — произвольная точка пространства. Если M ∈ λ, то Ax′ + By′ + Cz′ + D > 0, а если M ∈ µ, то Ax′ + By′ + Cz′ + D < 0.
|
| Точки P(x1, y1, z1) и Q(x2, y2, z2) расположены по одну сторону от плоскости Ax + By + Cz + D = 0 тогда и только тогда, когда числа Ax1 + By1 + Cz1 + D и Ax2 + By2 + Cz2 + D имеют одинаковый знак, и по разные стороны от этой плоскости тогда и только тогда, когда числа Ax1 + By1 + Cz1 + D и Ax2 + By2 + Cz2 + D имеют разные знаки.
|
d(M, σ) = 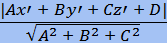 - расстояние от точки М до плоскости σ.
- расстояние от точки М до плоскости σ.
------Прямая в пространстве------
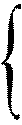
x = x0 + qt
y = y0 + rt - параметрические уравнения прямой в пространстве.
z = z0 + st
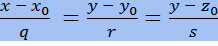 - канонические уравнения прямой в пространстве.
- канонические уравнения прямой в пространстве.
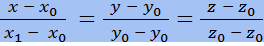 - уравнения прямой в пространстве по 2 точкам.
- уравнения прямой в пространстве по 2 точкам.
A1x + B1y + C1z + D1 = 0
- общие уравнения прямой в пространстве.
A2x + B2y + C2z + D2 = 0
Вектор
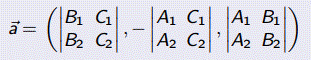 является направляющим вектором прямой, заданной общими уравнениями прямой в пространстве.
является направляющим вектором прямой, заданной общими уравнениями прямой в пространстве.
|
| Если прямая задана как пересечение двух плоскостей и известны уравнения этих плоскостей в прямоугольной декартовой системе координат, то в качестве направляющего вектора этой прямой можно взять векторное произведение главных векторов этих плоскостей.
|
Пусть плоскость σ задана уравнением Ax + By + Cz + D = 0, а прямая ℓ — уравнениями
 x = x0 + qt
y = y0 + rt
z = z0 + st
Тогда:
1) ℓ и σ пересекаются тогда и только тогда, когда Aq + Br + Cs
x = x0 + qt
y = y0 + rt
z = z0 + st
Тогда:
1) ℓ и σ пересекаются тогда и только тогда, когда Aq + Br + Cs 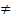 0;
2) ℓ и σ параллельны тогда и только тогда, когда Aq + Br + Cs = 0 и Ax0 + By0 + Cz0 + D 0;
2) ℓ и σ параллельны тогда и только тогда, когда Aq + Br + Cs = 0 и Ax0 + By0 + Cz0 + D 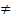 0;
3) ℓ лежит в σ тогда и только тогда, когда Aq + Br + Cs = 0 и Ax0 + By0 + Cz0 + D = 0. 0;
3) ℓ лежит в σ тогда и только тогда, когда Aq + Br + Cs = 0 и Ax0 + By0 + Cz0 + D = 0.
|
Пусть прямые ℓ1 и ℓ2 заданы уравнениями
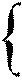 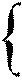
x = x1 + q1t x = x2 + q2t
y = y1 + r1t и y = y2 + r2t
z = z1 + s1t z = z2 + s2t
соответственно. Положим
|
| x2 - x1
| y2 - y1
| z2 - z1
| | ∆ =
| q1
| r1
| s1
| |
| q2
| r2
| s2
| 1) ℓ1 и ℓ2 скрещиваются тогда и только тогда, когда ∆ 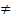 0; 0;
2) ℓ1 и ℓ2 пересекаются тогда и только тогда, когда ∆ = 0 и либо 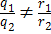 , либо , либо
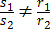 ; ;
3) ℓ1 и ℓ2 параллельны тогда и только тогда, когда ∆ = 0,
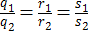 и либо и либо 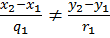 , либо , либо 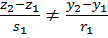 ; ;
4) ℓ1 и ℓ2 совпадают тогда и только тогда, когда ∆ = 0, 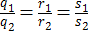 и и
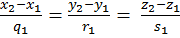 . .
|
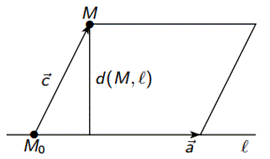
d(M, ℓ) = 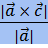 =
= 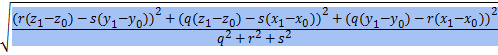 - расстояние от точки М до прямой ℓ.
- расстояние от точки М до прямой ℓ.
Пусть ℓ1 и ℓ2 — скрещивающиеся прямые. Общим перпендикуляром к прямым ℓ1 и ℓ2 называется прямая, перпендикулярная к каждой из прямых ℓ1 и ℓ2 и пересекающая каждую из них.
| Для произвольных скрещивающихся прямых ℓ1 и ℓ2 существует общий перпендикуляр к этим прямым.
|
Расстояние между скрещивающимися прямыми ℓ 1 и ℓ 2 - расстояние между точками, в которых общий перпендикуляр к скрещивающимся прямым ℓ1 и ℓ2 пересекает эти прямые.
d(ℓ1, ℓ2) = 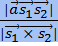
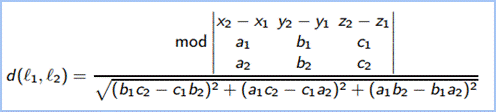
Если в пространстве заданы прямые с направляющими векторами (q1,r1,s1) и (q2,r2,s2), то угол α между этими прямыми:
cos α = 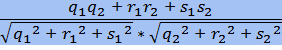
Если прямые на плоскости заданы уравнениями A1x + B1y + C1 = 0 и A2x + B2y + C2 = 0, то угол α между этими прямыми:
cos α = 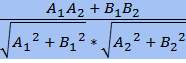
Если плоскости заданы уравнениями A1x + B1y + C1z + D1 = 0 и A2x + B2y + C2z + D2 = 0, то угол между этими плоскостями можно найти, вычисляя угол α между их главными векторами:
cos α = 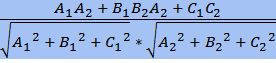
Если α — угол между ℓ и ℓ1, а β — острый угол между ℓ и ℓ2, то α + β = 90°. Пусть (q,r,s) — направляющий вектор прямой ℓ, а Ax + By + Cz + D = 0 — уравнение плоскости σ. Тогда прямая ℓ2 коллинеарна главному вектору (A, B, C) плоскости σ. Отсюда угол между прямой и плоскостью:
sin α = cos β = 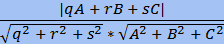
Тема 3: Комплексные числа
-----------Формула Кардано-----------
x = u + v = 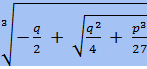 +
+ 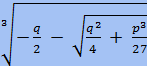 - формула Кардано (для уравнения вида
- формула Кардано (для уравнения вида 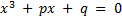 ).
).
Поле - неодноэлементное ассоциативное и коммутативное кольцо с 1, в котором все ненулевые элементы обратимы.
Поле комплексных чисел:
● содержит поле R действительных чисел;
● содержит квадратные корни из отрицательных чисел;
● не содержит ничего лишнего.
Системы линейных уравнений
Система линейных уравнений называется однородной, если свободные члены всех уравнений системы нулевые:
a11x1 + a12x2 +... + a1nxn = 0
a21x1 + a22x2 +... + a2nxn = 0
…
ak1x1 + ak2x2 +... + aknxn = 0
| Если x0 — некоторое решение системы Ax = b, то вектор-столбец x1 будет решением системы Ax = b тогда и только тогда, когда x1 = x0 + y, где y — решение соответствующей однородной системы Ax = 0.
|
| Множество решений однородной системы Ax = 0 образует подпространство в пространстве столбцов.
|
Фундаментальная системой решений - любой базис пространства, если пространство решений однородной системы ненулевое.
| Размерность пространства решений системы Ax = 0 равна n − r, где n — число неизвестных в системе, а r — ранг матрицы A.
|
b11y1 + b12y2 +... + b1ryr = - b1 r+1yr+1 -... - b1nyn
b21y1 + b22y2 +... + b2ryr = - b2 r+1yr+1 -... - b2nyn
…
bk1y1 + bk2y2 +... + bkryr = - br r+1yr+1 -... - brnyn
Неизвестные yr+1,..., yn - свободные, а неизвестные y1,..., yr - связанные.
Процедура решения системы линейных уравнений:
● элементарными преобразованиями строк приводим матрицу A|b к ступенчатому виду;
● если ранг r матрицы A меньше ранга матрицы A|b, система Ax = b несовместна; если ранги равны, находим частное решение x0 этой системы;
● находим фундаментальную систему решений x1,..., xn−r соответствующей однородной системы Ax = 0;
● выражение x = x0 + c1x1 + c2x2 + · · · + cn−rxn−r, где c1, c2,..., cn−r — произвольные скаляры, дает общее решение системы Ax = b. Каждое решение системы получается из общего при некотором (однозначно определяемом) наборе c1, c2,..., cn−r.
Тема 6: Евклидовы и унитарные пространства
Метод наименьших квадратов
Псевдорешение системы линейных уравнений Ax = b — это вектор x0, минимизирующий расстояние между векторами Ax и b.
Если псевдорешение неединственно, то обычно интересуются псевдорешением наименьшей длины - нормальное псевдорешение.
Метод наименьших квадратов - простое соображение, которое позволяет находить псевдорешения без вычисления ортогональной проекции.
Пусть A — k × n матрица над ℝ, а S — образ линейного отображения x ↦ Ax пространства 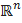 в пространство в пространство 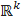 . Для произвольного вектора b ∈ . Для произвольного вектора b ∈ 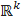 системы линейных уравнений Ax = bS и системы линейных уравнений Ax = bS и 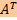 Ax = Ax = 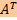 b равносильны. b равносильны.
|
Для любой матрицы A над ℝ ее ранг равен рангу матрицы 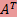 A. A.
|
-----Линейные функционалы-----
Пусть V — векторное пространство над произвольным полем F.
Линейный функционал на V — это линейное отображение 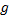 : V → F.
: V → F.
| Пусть V — конечномерное пространство со скалярным произведением над полем
F ∈ { ℝ, ℂ}, а Ф: V → F — линейный функционал. Тогда существует единственный вектор a ∈ V такой, что Φ(x) = xa для каждого вектора x ∈ V.
|
Строение линейного функционала:
Ker(Φ) — подпространство размерности dim V − 1, а его ортогональное дополнение
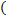 Ker(Φ)
Ker(Φ) 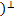 — одномерное подпространство в V.
— одномерное подпространство в V.
Фиксируем ненулевой вектор b ∈ 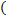 Ker(Φ)
Ker(Φ) 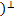 и пусть β:= Φ(b).
и пусть β:= Φ(b).
Положим a:= 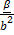 b и проверим, что Φ(x) = xa для каждого x ∈ V. Для этого представим x в виде x = c + γb для некоторого c ∈ Ker(Φ) и γ ∈ F. Такое представление возможно, так как V = Ker(Φ) ⊕
b и проверим, что Φ(x) = xa для каждого x ∈ V. Для этого представим x в виде x = c + γb для некоторого c ∈ Ker(Φ) и γ ∈ F. Такое представление возможно, так как V = Ker(Φ) ⊕ 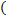 Ker(Φ)
Ker(Φ) 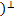 , а одномерное подпространство
, а одномерное подпространство 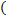 Ker(Φ)
Ker(Φ) 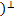 порождается вектором b. Тогда
порождается вектором b. Тогда
Φ(x) = Φ(c + γb) = Φ(c) + Φ(γb) = γΦ(b) = γβ,
поскольку Φ(c) = 0. С другой стороны,
xa = (c + γb) 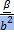 b = c
b = c 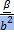 b + γb
b + γb 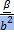 b = γβ,
b = γβ,
поскольку cb = 0.
---Сопряженное отображение---
Пусть  : V1 → V2 — линейное отображение (линейный оператор) пространств со скалярным произведением над полем F ∈ { ℝ, ℂ}.
: V1 → V2 — линейное отображение (линейный оператор) пространств со скалярным произведением над полем F ∈ { ℝ, ℂ}.
В каждом из пространств V1 и V2 — свое скалярное произведение: будем обозначать произведение векторов x, y ∈ V1 через x 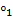 y, а произведение векторов p, q ∈ V2 — через p
y, а произведение векторов p, q ∈ V2 — через p 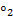 q.
q.
Возьмем произвольный вектор r ∈ V2 и свяжем с ним отображение Φr: V1 → F, определенное правилом Φr(x):=  x
x 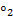 r. Отображение Φr — линейный функционал на пространстве V1.
r. Отображение Φr — линейный функционал на пространстве V1.
Пусть пространство V1 конечномерно. По теореме о строении линейного функционала существует однозначно определяемый вектор a ∈ V1 такой, что  x
x 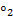 r = x
r = x 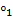 a для каждого x ∈ V1. Сопоставляя вектору r вектор a, получаем отображение из V2 в V1 - сопряженное отображением к
a для каждого x ∈ V1. Сопоставляя вектору r вектор a, получаем отображение из V2 в V1 - сопряженное отображением к 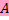 -
- 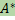 .
.
Ключевое тождество для сопряженного отображения:
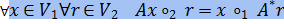
или же, если вернутся к привычному обозначению
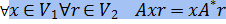
Тождество однозначно определяет сопряженное отображение, т.е. если для отображения 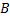 : V2 → V1 равенство : V2 → V1 равенство 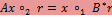 Br выполнено при всех x ∈ V1 и r ∈ V2, то Br выполнено при всех x ∈ V1 и r ∈ V2, то 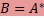 . .
|
Пусть  : V1 → V2 — линейное отображение пространств со скалярным произведением. Тогда сопряженное отображение : V1 → V2 — линейное отображение пространств со скалярным произведением. Тогда сопряженное отображение 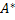 : V2 → V1 линейно. : V2 → V1 линейно.
|
Основные свойства взятия сопряженного отображения:
1) 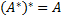 ;
2) ;
2) 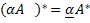 ;
3) ;
3) 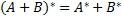 ;
4) ;
4) 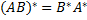 . .
|
Если линейное отображение  : V1 → V2 имеет в ортонормированных базисах пространств V1 и V2 матрицу : V1 → V2 имеет в ортонормированных базисах пространств V1 и V2 матрицу 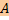 , то сопряженное ему отображение , то сопряженное ему отображение 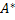 : V2 → V1 имеет в тех же базисах матрицу : V2 → V1 имеет в тех же базисах матрицу 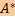 . .
|
Преобразование  : V → V называется самосопряженным, если
: V → V называется самосопряженным, если 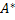 =
=  .
.
Тождество самосопряженных преобразований:
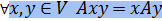
Если  — матрица самосопряженного преобразования A в некотором ортонормированном базисе, то
— матрица самосопряженного преобразования A в некотором ортонормированном базисе, то 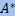 =
= 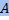 . Матрицы над ℂ со свойством
. Матрицы над ℂ со свойством 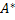 =
=  называются эрмитовыми.
называются эрмитовыми.
Для матриц над ℝ свойство 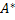 =
=  означает, что
означает, что 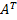 =
=  ; такие матрицы называются симметрическими.
; такие матрицы называются симметрическими.
Если линейное преобразование  : V → V имеет в некотором ортонормированном базисе пространства V эрмитову матрицу, то это преобразование самосопряженное. : V → V имеет в некотором ортонормированном базисе пространства V эрмитову матрицу, то это преобразование самосопряженное.
|
Если  : V1 → V2 — линейное отображение пространств со скалярным произведением, то : V1 → V2 — линейное отображение пространств со скалярным произведением, то 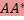 и и 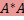 — самосопряженные преобразования. — самосопряженные преобразования.
|
Преобразование 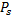 : V → V, сопоставляющее каждому вектору x ∈ V его ортогональную проекцию xS, называется ортогональным проектированием на S (ортопроектором).
: V → V, сопоставляющее каждому вектору x ∈ V его ортогональную проекцию xS, называется ортогональным проектированием на S (ортопроектором).
| Ортогональное проектирование на любое подпространство — самосопряженное преобразование.
|
Псевдообратное отображение
Теорема Фредгольма:
Если  : U → V — линейное отображение пространств со скалярным произведением над полем F ∈ { ℝ, ℂ}, то : U → V — линейное отображение пространств со скалярным произведением над полем F ∈ { ℝ, ℂ}, то 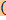 Im Im 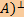 = Ker = Ker 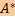 . .
|
Альтернатива Фредгольма:
Пусть A — n × k матрица над полем F ∈ { ℝ, ℂ}. Либо система линейных уравнений Ax = b имеет решение при любой правой части b ∈ 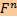 , либо сопряженная система
A ∗ y = 0 имеет нетривиальное решение y ∈ , либо сопряженная система
A ∗ y = 0 имеет нетривиальное решение y ∈ 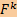 \ {0}. \ {0}.
|
Пусть  : U → V — линейное отображение пространств со скалярным произведением. Теорема Фредгольма дает ортогональное разложение пространства V:
: U → V — линейное отображение пространств со скалярным произведением. Теорема Фредгольма дает ортогональное разложение пространства V:
V = Ker 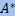 ⊕ Im
⊕ Im 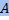 .
.
Применяя ту же теорему к сопряженному отображению 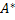 : V → U, получим ортогональное разложение пространства U:
: V → U, получим ортогональное разложение пространства U:
U = Ker 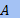 ⊕ Im
⊕ Im 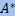 .
.
Положим U0:= Im 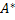 , V0:= Im
, V0:= Im  и обозначим через
и обозначим через  0 ограничение отображения
0 ограничение отображения  на подпространство U0. Это означает, что вектор
на подпространство U0. Это означает, что вектор  0x определен, только если x ∈ U0, и в этом случае
0x определен, только если x ∈ U0, и в этом случае  0x:=
0x:=  x.
x.
 0 — взаимно однозначное отображение U0 на V0. 0 — взаимно однозначное отображение U0 на V0.
|
Если A — матрица линейного отображения  : U → V в некоторых ортонормированных базисах пространств U и V, то матрица псевдообратного отображения
: U → V в некоторых ортонормированных базисах пространств U и V, то матрица псевдообратного отображения 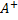 : V → U в тех же базисах называется псевдообратной к матрице A - A
: V → U в тех же базисах называется псевдообратной к матрице A - A 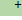 .
.
Для любой системы линейных уравнений Ax = b над полем F ∈ { ℝ, ℂ} формула
x = A 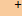 b возвращает ее нормальное псевдорешение.
Теорема Пенроуза:
Отображение b возвращает ее нормальное псевдорешение.
Теорема Пенроуза:
Отображение 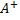 удовлетворяет следующим тождествам:
1) удовлетворяет следующим тождествам:
1) 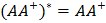 2)
2) 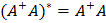 3)
3) 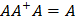 4)
4) 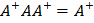 Обратно, если некоторое линейное отображение
Обратно, если некоторое линейное отображение 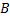 удовлетворяет тождествам 1)–4) c удовлетворяет тождествам 1)–4) c 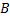 , подставленным вместо , подставленным вместо 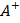 , то , то 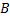 = = 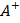 . .
|
| Скелетное разложение:
Пусть A — n × k матрица ранга r над произвольным полем. Тогда A = BC, где B —
n × r матрица ранга r, a C — r × k матрица ранга r.
|
Примеры задач
Линейные операции над векторами
Отрезок AB называется направленным, если указано, какая из точек A или B является его началом, а какая — концом. Направленный отрезок с началом в точке A и концом в точке B - 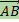 .
.
Длина направленного отрезка 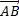 - |
- | 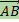 |.
|.
Если A = B, то отрезок называется нулевым - 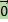 .
.
Направленный отрезок 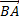 называется противоположным к
называется противоположным к 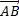 .
.
Ненулевые направленные отрезки, лежащие на одной прямой или на параллельных прямых, называются коллинеарными - 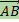 ||
|| 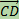 .
.
Коллинеарные направленные отрезки называются сонаправленными (прямо коллинеарными), если они направлены в одну и ту же сторону - 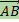 ⇈
⇈ 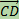 , и противонаправленными (обратно коллинеарными) в противоположном случае -
, и противонаправленными (обратно коллинеарными) в противоположном случае - 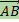 ↑↓
↑↓ 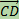 .
.
| Нулевой направленный отрезок по определению считается коллинеарным, сонаправленным и противонаправленным любому направленному отрезку.
|
Вектор — это множество всех направленных отрезков, имеющих одинаковую длину и одинаковое направление.
Изображение вектора - направленный отрезок, принадлежащий вектору.
Длина (модуль) вектора - длина любого его изображения.
| Два вектора равны, если они равны как множества, т. е. состоят из одних и тех же направленных отрезков (если они имеют одинаковую длину и одинаковое направление).
|
Два вектора называются коллинеарными [сонаправленными, противонаправленными], если их изображения коллинеарны [сонаправленны, противонаправленны].
Если отрезок 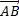 является изображением вектора
является изображением вектора  , то вектор, изображением которого является отрезок
, то вектор, изображением которого является отрезок 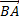 , называется противоположным вектору
, называется противоположным вектору  - −
- − 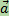 .
.
Нулевой вектор - вектор, изображением которого является нулевой направленный отрезок - 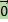 .
.
| Нулевой вектор коллинеарен, сонаправлен и противонаправлен с любым другим вектором.
|
Пусть даны вектора  и
и  . Зафиксируем точку O, отложим от нее вектор
. Зафиксируем точку O, отложим от нее вектор  , обозначим конец полученного направленного отрезка через A. От точки A отложим вектор
, обозначим конец полученного направленного отрезка через A. От точки A отложим вектор  , обозначим конец полученного направленного отрезка через B. Тогда отрезок
, обозначим конец полученного направленного отрезка через B. Тогда отрезок 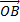 изображает вектор, который называется суммой векторов
изображает вектор, который называется суммой векторов  и
и  -
- 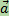 +
+ 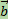 .
.

Свойства суммы векторов:
Если  , ,  и и 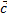 — произвольные вектора, то:
1) — произвольные вектора, то:
1)  + +  = =  + +  (сложение векторов коммутативно);
2) ( (сложение векторов коммутативно);
2) ( + +  ) + ) + 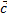 = =  + ( + ( + + 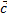 ) (сложение векторов ассоциативно);
3) ) (сложение векторов ассоциативно);
3)  + + 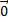 = =  ;
4) ;
4)  + (− + (−  ) = ) = 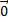 .
Таким образом, множество всех векторов с операцией их сложения является абелевой группой. Нейтральным элементом этой группы является вектор .
Таким образом, множество всех векторов с операцией их сложения является абелевой группой. Нейтральным элементом этой группы является вектор 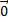 , а вектором, обратным к , а вектором, обратным к  , — вектор − , — вектор −  . .
|
Произведением вектора 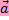 на число t называется вектор t
на число t называется вектор t  такой, что:
такой, что:
1) |t~a | = |t| · | ~a |;
2) если t > 0, то t  ⇈
⇈  , а если t < 0, то t
, а если t < 0, то t  ↑↓
↑↓  .
.
Операции сложения векторов и умножения вектора на число часто объединяют термином линейные операции над векторами.
Свойства произведения вектора на число:
Если  и и  — произвольные вектора, а t и s — произвольные числа, то:
1) t( — произвольные вектора, а t и s — произвольные числа, то:
1) t( + +  ) = t ) = t  + t + t  (умножение вектора на число дистрибутивно относительно сложения векторов);
2) (t + s) (умножение вектора на число дистрибутивно относительно сложения векторов);
2) (t + s)  = t = t  + s + s  (умножение вектора на число дистрибутивно относительно сложения чисел);
3) t(s (умножение вектора на число дистрибутивно относительно сложения чисел);
3) t(s  ) = (ts) ) = (ts)  ;
4) 1 · ;
4) 1 ·  = =  ;
5) (−1) · ;
5) (−1) ·  = − = −  . .
|
Пусть  — ненулевой вектор. Ортом вектора
— ненулевой вектор. Ортом вектора  называется вектор длины 1, сонаправленный с вектором
называется вектор длины 1, сонаправленный с вектором  . Если
. Если  — ненулевой вектор, то вектор
— ненулевой вектор, то вектор 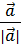 является ортом вектора
является ортом вектора  .
.



 — вектор. Его проекцией на ось ℓ называется число, обозначаемое пр
— вектор. Его проекцией на ось ℓ называется число, обозначаемое пр 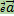 и определяемое следующим образом:
и определяемое следующим образом: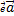 := 0.
:= 0.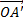 |, если
|, если 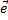

 — произвольные вектора, а t — произвольное число, то:
1) пр
— произвольные вектора, а t — произвольное число, то:
1) пр 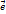 (
(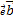 ;
2) пр
;
2) пр 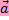 — угол между направляющим вектором оси и
— угол между направляющим вектором оси и 
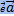 = |
= | 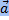 | cos(
| cos(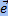 )
)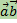 .
.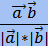
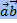 = |
= | 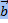 | · cos(
| · cos(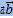 = |
= | 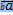
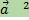 .
.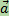 ⊥
⊥ 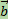 .
.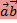 = 0.
= 0.
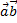 > 0;
б) прямым тогда и только тогда, когда
> 0;
б) прямым тогда и только тогда, когда 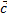 — произвольные вектора, а t — произвольное число, то:
1)
— произвольные вектора, а t — произвольное число, то:
1) 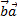 (скалярное произведение коммутативно);
2) (
(скалярное произведение коммутативно);
2) (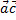 +
+ 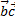 (скалярное произведение дистрибутивно относительно сложения векторов);
3) (t
(скалярное произведение дистрибутивно относительно сложения векторов);
3) (t 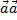 ≥ 0, причем
≥ 0, причем 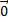 .
.
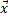 выполняется равенство
выполняется равенство 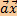 =
= 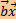 , то
, то 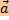 =
= 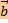 .
.
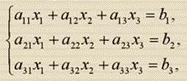
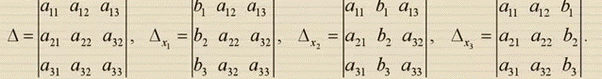
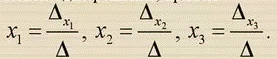
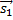 = (−B, A, 0),
= (−B, A, 0), 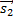 = (−C, 0, A) и
= (−C, 0, A) и 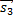 = (0, −C,B). Тогда по крайней мере два из векторов
= (0, −C,B). Тогда по крайней мере два из векторов 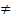 0, то этими свойствами обладают вектора
0, то этими свойствами обладают вектора 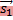 и
и 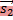 , если B
, если B 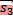 , а если C
, а если C 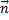 = (A,B,C) называется главным вектором плоскости π.
= (A,B,C) называется главным вектором плоскости π.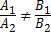 или
или 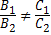 ;
2) параллельны тогда и только тогда, когда
;
2) параллельны тогда и только тогда, когда 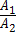 =
= 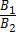 =
= 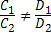 ;
3) совпадают тогда и только тогда, когда
;
3) совпадают тогда и только тогда, когда 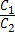 =
= 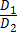 .
.

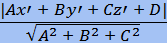 - расстояние от точки М до плоскости σ.
- расстояние от точки М до плоскости σ.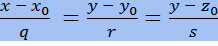 - канонические уравнения прямой в пространстве.
- канонические уравнения прямой в пространстве.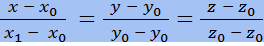 - уравнения прямой в пространстве по 2 точкам.
- уравнения прямой в пространстве по 2 точкам.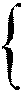
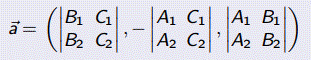 является направляющим вектором прямой, заданной общими уравнениями прямой в пространстве.
является направляющим вектором прямой, заданной общими уравнениями прямой в пространстве.
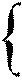 x = x0 + qt
y = y0 + rt
z = z0 + st
Тогда:
1) ℓ и σ пересекаются тогда и только тогда, когда Aq + Br + Cs
x = x0 + qt
y = y0 + rt
z = z0 + st
Тогда:
1) ℓ и σ пересекаются тогда и только тогда, когда Aq + Br + Cs 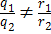 , либо
, либо 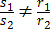 ;
;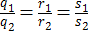 и либо
и либо 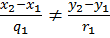 , либо
, либо 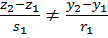 ;
;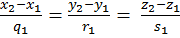 .
.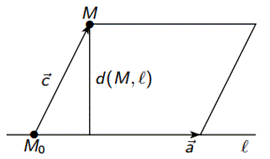
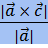 =
= 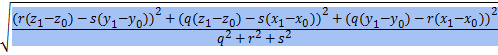 - расстояние от точки М до прямой ℓ.
- расстояние от точки М до прямой ℓ.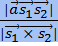
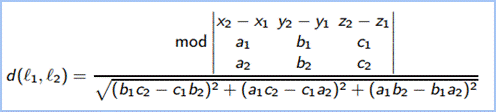
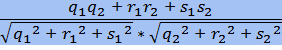
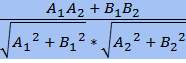
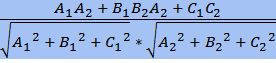
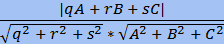
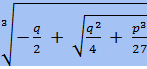 +
+ 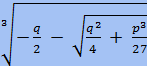 - формула Кардано (для уравнения вида
- формула Кардано (для уравнения вида 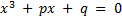 ).
).
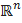 в пространство
в пространство 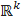 . Для произвольного вектора b ∈
. Для произвольного вектора b ∈ 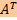 Ax =
Ax = 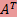 A.
A.
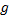 : V → F.
: V → F. Ker(Φ)
Ker(Φ) 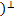 — одномерное подпространство в V.
— одномерное подпространство в V.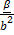 b и проверим, что Φ(x) = xa для каждого x ∈ V. Для этого представим x в виде x = c + γb для некоторого c ∈ Ker(Φ) и γ ∈ F. Такое представление возможно, так как V = Ker(Φ) ⊕
b и проверим, что Φ(x) = xa для каждого x ∈ V. Для этого представим x в виде x = c + γb для некоторого c ∈ Ker(Φ) и γ ∈ F. Такое представление возможно, так как V = Ker(Φ) ⊕ 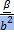 b = c
b = c  : V1 → V2 — линейное отображение (линейный оператор) пространств со скалярным произведением над полем F ∈ { ℝ, ℂ}.
: V1 → V2 — линейное отображение (линейный оператор) пространств со скалярным произведением над полем F ∈ { ℝ, ℂ}.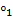 y, а произведение векторов p, q ∈ V2 — через p
y, а произведение векторов p, q ∈ V2 — через p 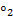 q.
q.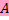 -
- 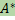 .
.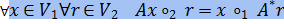
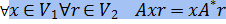
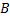 : V2 → V1 равенство
: V2 → V1 равенство 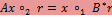 Br выполнено при всех x ∈ V1 и r ∈ V2, то
Br выполнено при всех x ∈ V1 и r ∈ V2, то 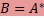 .
.
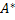 : V2 → V1 линейно.
: V2 → V1 линейно.
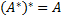 ;
2)
;
2) 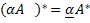 ;
3)
;
3) 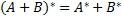 ;
4)
;
4) 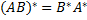 .
.
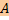 , то сопряженное ему отображение
, то сопряженное ему отображение 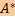 .
.
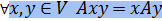
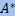 =
= 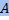 . Матрицы над ℂ со свойством
. Матрицы над ℂ со свойством 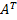 =
= 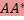 и
и 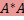 — самосопряженные преобразования.
— самосопряженные преобразования.
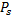 : V → V, сопоставляющее каждому вектору x ∈ V его ортогональную проекцию xS, называется ортогональным проектированием на S (ортопроектором).
: V → V, сопоставляющее каждому вектору x ∈ V его ортогональную проекцию xS, называется ортогональным проектированием на S (ортопроектором). Im
Im 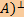 = Ker
= Ker 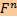 , либо сопряженная система
A ∗ y = 0 имеет нетривиальное решение y ∈
, либо сопряженная система
A ∗ y = 0 имеет нетривиальное решение y ∈ 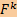 \ {0}.
\ {0}.
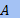 ⊕ Im
⊕ Im 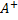 : V → U в тех же базисах называется псевдообратной к матрице A - A
: V → U в тех же базисах называется псевдообратной к матрице A - A 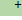 .
.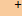 b возвращает ее нормальное псевдорешение.
Теорема Пенроуза:
Отображение
b возвращает ее нормальное псевдорешение.
Теорема Пенроуза:
Отображение 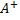 удовлетворяет следующим тождествам:
1)
удовлетворяет следующим тождествам:
1) 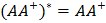 2)
2) 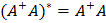 3)
3) 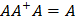 4)
4) 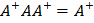 Обратно, если некоторое линейное отображение
Обратно, если некоторое линейное отображение 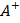 , то
, то 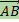 .
.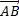 - |
- | 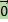 .
.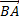 называется противоположным к
называется противоположным к 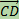 .
.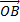 изображает вектор, который называется суммой векторов
изображает вектор, который называется суммой векторов 
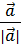 является ортом вектора
является ортом вектора 


