
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема: Способы вычисления интегралов.
Краткое изложение темы. Определение: Множество всех первообразных функций f(x) в промежутке х называется неопределенным интегралом этой функции и обозначается так Свойства неопределенного интеграла: 1.
2. 3. 4. 5. Основные формулы интегрирования.
Метод замены переменной. Пусть имеем
и x = φ(t) – непрерывно дифференцированная. Рассмотрим Итак, функция F(φ(t)) – есть первообразная для Следовательно:
Из (1) и (2) получаем следующее равенство.
На практике замену переменных производят, как правило, t = g(x). Определенный интеграл Определение. Приращение F(b) — F(a) любой из первообразных функций F(х) + С при изменении аргумента от х = а до х = b называется определенным интегралом и обозначается
Примеры выполнения заданий. Пример 1. Вычислить Решение: Согласно правилу имеем: Ответ: Пример 2. Вычислить Решение:
Ответ: Пример 3. Найти: Решение:
Ответ: Пример 4. Найти: Решение:
Ответ: Пример 5. Найти Решение: Вынесем множитель
Положим
тогда Находим новые пределы:
Следовательно
Ответ:
Задания для практической работы. Вариант 1. Найдите следующие интегралы:
Практическая работа № 9. Тема: Решение дифференциальных уравнений. Задания для подготовки к практической работе. Вспомнить правила интегрирования функций, свойства логарифмов (Смотрите приложение). Краткое изложение темы. Уравнение вида
связывающее аргумент Решением дифференциального уравнения называется такая функция, которая обращает это уравнение в тождество. Дифференциальным уравнением первого порядка называется уравнение вида
где Общее решение уравнений имеет вид Частным решением называется решение, полученное из общего при различных числовых значениях произвольных постоянных.
Дифференциальным уравнением с разделяющимися переменными называется уравнение вида
Для решения этого уравнения нужно сначала разделить переменные
а затем проинтегрировать обе части полученного равенства
Линейным дифференциальным уравнением первого порядка называется уравнение вида
где Это уравнение приводится к уравнению с разделяющимися переменными с помощью подстановки Примеры выполнения заданий. 1. Дифференциальные уравнения с разделяющимися переменными. Пример 1. Найти общее решение уравнения Решение: 1) Разделим переменные
2) Интегрируем обе части полученного уравнения:
Так как произвольная постоянная С может принимать любые числовые значения, то для удобства дальнейших преобразований вместо С написали
Это и есть общее решение данного уравнения. Ответ:
Пример 2. Найти частное решение уравнения Решение: 1) Разделим переменные
2) Интегрируем обе части полученного уравнения:
3) Для нахождения значения произвольной постоянной С подставим значения
Следовательно, искомое частное решение, удовлетворяющее указанным начальным условиям, имеет вид Ответ:
2. Линейные дифференциальные уравнения первого порядка. Пример 3. Найти общее решение уравнения Решение: Это линейное уравнение: здесь Положим
Подставив теперь выражения для
или
Так как одну из вспомогательных функций Разделим в этом уравнении переменные:
Интегрируем обе части уравнения:
(произвольную постоянную С принимаем равной 0, так как находим одно из частных решений)
Подставим теперь выражение для
Разделим переменные
Интегрируем обе части уравнения
Отсюда находим
Зная
Ответ:
Пример 4. Найти частное решение уравнения Решение: Разделив все члены данного уравнения на
Положим Подставив теперь выражения для
Для отыскания
Разделим переменные:
Интегрируем обе части уравнения:
Подставляя выражение для
Разделяем переменные
Интегрируем обе части уравнения
Общее решение данного уравнения:
Используя начальные условия Таким образом, искомое частное решение имеет вид
Ответ: Задания для практической работы. Вариант 1. 1. Найдите общее решение уравнения 2. Найдите частное решение уравнения 3. Найдите общее решение уравнения 4. Найдите частное решение уравнения Практическая работа № 10.
|
||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-01-08; просмотров: 118; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.228.35 (0.06 с.) |
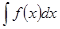 .
.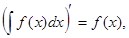 имеем
имеем
 (подынтегральному выражению).
(подынтегральному выражению). где k – постоянная.
где k – постоянная.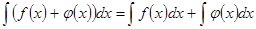

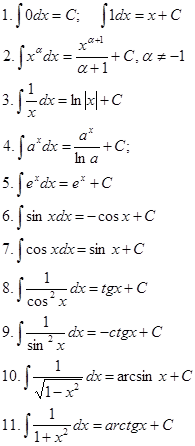
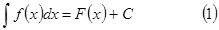
 - первообразная для f(x)∙φ′(t).
- первообразная для f(x)∙φ′(t).
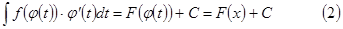
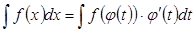 - формула замены переменной в неопределенном интеграле.
- формула замены переменной в неопределенном интеграле. .
.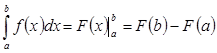 - формула Ньютона-Лейбница.
- формула Ньютона-Лейбница. .
.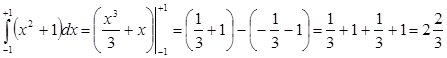 .
.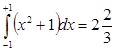
 .
.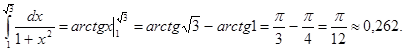
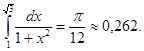
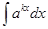
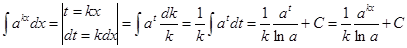




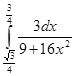 .
.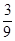 за знак интеграла:
за знак интеграла: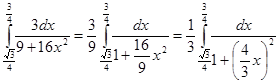 .
.
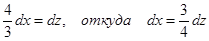 .
.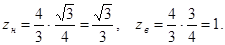
 .
.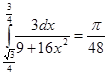 .
.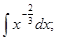
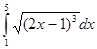
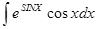
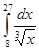
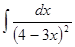

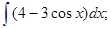


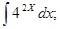
 ,
,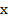 , неизвестную функцию
, неизвестную функцию 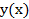 и ее производные, называется дифференциальным уравнением.
и ее производные, называется дифференциальным уравнением.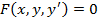
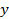 — неизвестная функция;
— неизвестная функция; 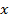 — независимая переменная.
— независимая переменная.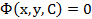 .
. .
. ,
, .
.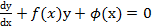 ,
, и
и 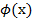 - функции от х.
- функции от х. , где
, где 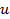 и
и  - новые функции от х.
- новые функции от х.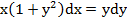 .
.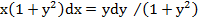 , тогда
, тогда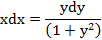
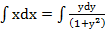 ;
;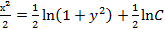 .
. .
.
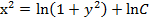
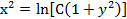
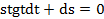 , удовлетворяющее начальным условиям
, удовлетворяющее начальным условиям 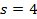 при
при 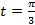 .
.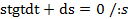

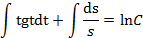
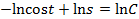
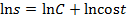
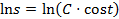
 - это общее решение данного уравнения.
- это общее решение данного уравнения.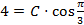 ,
,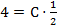 ,
,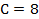 .
.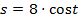 .
.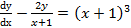 .
.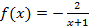 ,
,  .
. и продифференцируем это равенство по х:
и продифференцируем это равенство по х: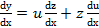 .
.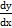 в данное уравнение, получим
в данное уравнение, получим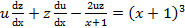 ,
,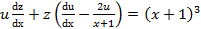 . (*)
. (*)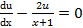 .
.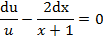
 ,
, ,
,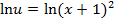 ,
, .
.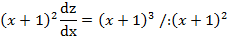
 .
.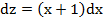
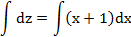

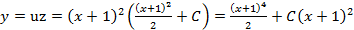 .
.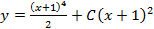 .
. , если
, если 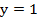 при
при 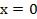 .
. , получим уравнение
, получим уравнение , которое является линейным.
, которое является линейным.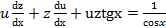 ,
, . (*)
. (*)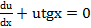 ,
,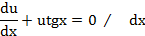
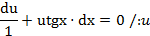
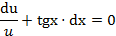
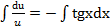 ,
, ,
,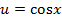 .
.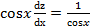 ,
,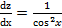 ,
,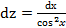 ,
,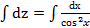 ,
, .
.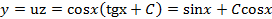 .
.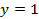 ,
, 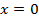 , имеем
, имеем  , откуда
, откуда  .
. .
.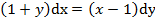 .
.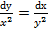 , удовлетворяющего начальным условиям
, удовлетворяющего начальным условиям 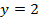 при
при 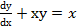 .
. , удовлетворяющего начальным условиям
, удовлетворяющего начальным условиям 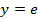 при
при  .
.


