Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ:  Археология Биология Генетика География Информатика История Логика Маркетинг Математика Менеджмент Механика Педагогика Религия Социология Технологии Физика Философия Финансы Химия ЭкологияТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Геометрические характеристики поперечных сечений бруса
При решении задач, связанных с изгибом, необходимо знать некоторые геометрические характеристики поперечного сечения. Статические моменты сечения. Некоторое поперечное сечение бруса произвольной формы (рис. 2.11) свяжем с системой координат xy и рассмотрим два интеграла
Каждый из интегралов представляет собой сумму произведений элементарных площадок на расстояние до соответствующей оси (x или y). Первый интеграл называется статическим моментом сечения относительно оси x, а второй — относительно оси y. Рассмотрим, как изменятся статические моменты относительно параллельных осей. Пусть расстояние между осями x 1 и x 2 равно b, а между осями y 1 и y 2 равно а (рис. 2.12).
Положим, что площадь сечения S и статические моменты относительно осей x 1 и y 1 заданы. Требуется определить статические моменты относительно осей x 2 и y 2. Из рисунка видно, что x 2 = x 1 - а, а y 2 = y 1 - b. Искомые статические моменты будут равны
или sx 2 = sx 1 - bS; sy 2 = sy 1 - aS. Следовательно, при параллельном переносе осей статический момент меняется на величину, равную произведению площади S на расстояние между осями. Всегда можно подобрать a и b (причем единственным образом) так, чтобы sx 1 - bS = 0 и sу 1 - аS = 0, т. е. статические моменты относительно осей x 2 и y 2 обращаются в нуль. Ось, относительно которой статический момент равен нулю, называется центральной, а точка пересечения центральных осей называется центром тяжести сечения. Расстояние до центральных осей от произвольно взятых определяется зависимостями b = yС = sx 1/ S; а = xС = sу 1/ S. Статический момент относительно любой оси, проходящей через центр тяжести сечения, равен нулю. Размерность статических моментов — миллиметр в кубе (мм3). Пример 2.6 Найти, на каком расстоянии от основания расположен центр тяжести треугольника (рис. 2.13).
Решение. 1. Начало координат выбираем в произвольной точке О, а ось x 1 совмещаем с основанием треугольника.
2. Вычисляем статический момент треугольника относительно оси x 1:
Элементарная площадка dS = ldy 1. Из подобия треугольников получаем l = B (H - y 1)/ H. Таким образом, статический момент относительно оси x 1
3. Определяем расстояние от центра тяжести до основания треугольника, если площадь треугольника S = BH /2:
Пример 2.7 Определить положение центра тяжести для плоского сечения, составленного из трех фигур (рис. 2.14): швеллера № 20У (ГОСТ 8240—97), уголка № 10 (ГОСТ 8509—93) и полосы, размеры которой представлены на чертеже.
Решение. 1. Проставим номера фигур. 2. Оси координат x 1 и y 1 направляем, как указано на рисунке. 3. Определим геометрические характеристики фигур, входящих в сложное составное сечение: а) швеллер № 20У — поз. 1. Выписываем из ГОСТ 8240—97 геометрические характеристики: S 1 = 23,4 см2; x 1 С = 10 см; y 1 С = 2,07 см (см. Приложение III); б) уголок № 10 — поз. 2. Выписываем из ГОСТ 8509—93 (см. Приложение I) геометрические характеристики для равнополочного уголка № 10 (100×100×12) и рассчитываем координаты его центра тяжести по отношению к выбранной системе отсчета: S 2 = 22,8 см2; x 2 C = 10 + (10 - 2,91) = 17,09 см; y 2 C = -2,91 см; в) полоса — поз. 3. Определяем ее геометрические характеристики: S 3 = 12·1 = 12 см2; x 3 С = -0,5 см; y 3 С = -1 см. 4. Запишем в табл. 2.2 рассчитанные (или взятые из стандартов) площади, координаты центров тяжестей и статические моменты плоских фигур, учитывая, что статический момент сечения i- й фигуры относительно оси x 1 six 1 = y 1 Ci Si, где y 1 Ci — координата центра тяжести сечения i -й фигуры относительно оси x 1; Si — площадь фигуры; статический момент сечения i -й фигуры относительно оси y 1: siу 1 = x 1 Ci Si, где x 1 Ci — координата центра тяжести сечения i- й фигуры относительно оси y 1.
5. Вычисляем координаты центра тяжести С сложного составного сечения:
Моменты инерции сечения. Рассмотрим три интеграла
где через x и y обозначены текущие координаты элементарной площадки dS (см. рис. 2.11) в произвольно взятой системе координат. Первые два интеграла называются осевыми моментами инерции сечения соответственно относительно осей x и y, а третий интеграл — центробежным моментом инерции сечения относительно осей x, y. Осевые моменты всегда положительны, а центробежный момент инерции может быть как положительным, так и отрицательным (в зависимости от расположения сечения относительно осей x, y). Рассмотрим, как изменятся значения моментов инерции сечения при параллельном переносе осей. Положим, что заданы статические моменты и моменты инерции относительно осей x 1 и y 1. Требуется определить моменты инерции относительно осей x 2 и y 2 (см. рис. 2.12):
Подставим значения x 2 = x 1 - а и y 2 = y 1 - b в подынтегральную функцию:
После раскрытия скобок получаем
Если оси x 1 и y 1 — центральные, то sx 1 и sy 1 равны нулю. В этом случае полученные зависимости упрощаются:
Следует запомнить, что при переходе от центральных осей к нецентральным осевые моменты инерции увеличиваются и величины b 2 S и a 2 S нужно к моментам инерции прибавлять, в противоположном случае — вычитать. При определении центробежных моментов инерции следует учитывать знаки величин а и b. Однако при параллельном переносе осей можно установить, в какую сторону меняется Jxy. Площади сечения, находящиеся в I и III квадрантах систем координат, дают положительное значение центробежного момента, а находящиеся во II и IV квадрантах — отрицательные. Поэтому при переносе осей следует установить, в каких квадрантах площади сечения увеличиваются. Например, если при переходе от центральных осей возрастает площадь во втором квадранте, то центробежный момент инерции уменьшается, следовательно, произведение abS из центрального центробежного момента нужно вычесть. Размерность моментов инерции — миллиметр в четвертой степени (мм4). Пример 2.8 Найти момент инерции треугольника (см. рис. 2.13) относительно основания и относительно центральной оси, параллельной основанию. Решение. 1. Вычислим момент инерции относительно оси x 1:
Из подобия треугольников имеем l = В (H - y 1)/ H. Подставим это выражение в подынтегральную функцию
откуда Jx 1 = ВН 3/12. 2. Определяем момент инерции относительно центральной оси. Как было сказано ранее, центральный момент инерции всегда меньше момента инерции относительно других параллельных, но не центральных осей. Следовательно, чтобы найти центральный момент инерции относительно оси x, нужно вычесть b 2 S из Jx 1. В этом случае Jx = Jx 1 - (H /3)2 S или Jx = BH 3/36. Главные оси и главные моменты инерции. Пусть известны моменты инерции Jx, Jy и Jxy относительно нецентральных осей x, y. Необходимо установить зависимость между этими моментами инерции и моментами инерции относительно осей u и v, которые повернуты относительно осей x и y на угол a (рис. 2.15). Положение элементарной площади плоской фигуры dS относительно общего начала двух систем координат определяет радиус-вектор r. Его проекции на оси координат u, v связаны с его же проекциями на оси x, y следующими зависимостями:
u = y sin a + x cos a; v = y cos α - x sin a.
Запишем выражения для моментов инерции сечения относительно осей u и v:
и подставим вместо координат u и v полученные ранее зависимости. Тогда
откуда
Сложим почленно первые два равенства, в результате чего имеем Ju + Jv = Jx + Jy. Таким образом, сумма осевых моментов инерции относительно двух взаимно-перпендикулярных осей не зависит от угла a и при повороте остается постоянной. Кроме того, сумма осевых моментов инерции может быть записана следующим образом:
Известно, что интеграл Ju + Jv = Jp. Для круглого сечения Jx = Jy и осевой момент инерции в два раза меньше полярного:
Еще раз заметим, что при повороте осей каждая из величин Ju и Jv изменяется, но их сумма остается неизменной. Следует предположить, что при некотором угле поворота один из осевых моментов достигает своего минимального значения, а другой — максимального. Такой угол можно найти, взяв производную от Ju по углу поворота и приравняв ее к нулю:
Мы написали уравнение, из которого можно определить угол поворота a, при котором осевой момент инерции Ju принимает экстремальные значения: максимальное и минимальное. Решая это уравнение, получаем
Если подставить значение этого угла в выражение для определения центробежного момента инерции Juv относительно этих осей, то он обращается в нуль. Оси, относительно которых центробежный момент инерции равен нулю, а осевые моменты принимают экстремальные значения, называются главными, а осевые моменты инерции относительно главных осей называются главными моментами инерции. Если главные оси являются центральными, то они называются главными центральными осями, а моменты инерции — главными центральными моментами инерции.
Если сечение имеет ось симметрии (например, круг, прямоугольник), то эта ось всегда будет главной, так как центробежный момент инерции относительно нее равен нулю (центробежный момент инерции части сечения, расположенного по одну сторону от оси симметрии равен моменту части, расположенной по другую, но с обратным знаком). Пример 2.9 Найти момент инерции прямоугольника относительно основания и центральной оси, параллельной основанию; размеры прямоугольника указаны на рис. 2.16.
Решение. 1. Проводим оси координат: через центр тяжести сечения x, y; вдоль основания и по перпендикулярной к нему стороне x 1, y 1. 2. Выделяем элементарную площадку dS = Вdy 1. 3. Определяем момент инерции прямоугольника относительно оси x 1:
4. Определяем центральный момент инерции относительно оси x. Центральный момент инерции всегда меньше моментов инерции относительно оси, параллельной центральной. Следовательно:
Определив положение главных осей, необходимо установить зависимости, которые позволят вычислять главные моменты инерции. Для этого в результате тригонометрических преобразований получаем
Далее, учитывая тригонометрические соотношения
а также зависимость
Знак «+» соответствует максимальному моменту инерции, знак «-» — минимальному. Пример 2.10 Для сечения, составленного из швеллера № 20У (ГОСТ 8240—97), равнополочного уголка № 10 (100×100×12) (ГОСТ 8509—93) и полосы, размеры которой проставлены на рис. 2.14, определить главные центральные моменты инерции. Решение. 1. Разбиваем сечение на простейшие фигуры, для которых моменты инерции можно определить или взять из стандартов. 2. Проставляем номера позиций. 3. Определяем положение центра тяжести сечения (см. пример 2.7). 4. Через найденный центр тяжести сечения C проводим центральные оси x, y. 5. Вычисляем моменты инерции отдельных фигур относительно собственных центральных осей: а) швеллер № 20У (поз. 1) — выписываем из стандарта его моменты инерции: JxС 1 = 113 см4, JyС 1 = 1520 cм4. Центробежный момент инерции швеллера будет равен нулю, так как он имеет одну ось симметрии. Заносим данные в табл. 2.3.
Продолжение табл. 2.3
Кроме того, внесем в эту таблицу размеры a, b и другие, которые облегчат расчеты (см. табл. 2.3); б) уголок № 10 (поз. 2) — выписываем из стандарта JxС 2 = JyС 2 = 209 см4. Центробежный момент инерции для равнополочного уголка определяем следующим образом. Во-первых, нужно установить знак центробежного момента. Если провести центральные оси через С 2, то станет ясно, что бо́льшая часть площади сечения уголка находится во втором и четвертом квадрантах, следовательно, центробежный момент будет отрицательным. Далее воспользуемся формулой (с учетом того, что для данного уголка JxС 2 = JyС 2)
Откуда Jxy = Ju - Jx. Наибольший главный осевой момент инерции для уголка данного номера Ju = = 331 см4 (см. ГОСТ 8509—93). Таким образом, Jxy = 331 - 209 = 122 см4. Заносим в табл. 2.3 значение центробежного момента уголка относительно собственных центральных осей со знаком «-»; в) полоса — поз. 3. Определяем осевой момент инерции относительно центральной оси х, проходящей через С 3:
Центробежный момент инерции полосы равен нулю, так как она имеет ось симметрии. 6. Заполняем все графы табл. 2.3. 7. Определяем угол, на который нужно повернуть центральные оси сечения x и y, проходящие через центр С, чтобы они стали главными:
Таким образом,
Следовательно, a = 7°20′. Знак «-» означает, что нужно повернуть оси x, y по часовой стрелке. 8. Вычисляем главные центральные моменты инерции
Как ранее отмечалось, сумма моментов инерции не должна изменяться при повороте осей, т. е. Ju + Jv = Jx + Jy, или 697,7 + 4234,5 = 755,6 + 4176,6. Проверка показала, что расчет выполнен верно. Прямой поперечный изгиб Под изгибом понимается такой вид нагружения, при котором в поперечных сечениях бруса возникают изгибающие моменты (см. подразд. 2.1). Если изгибающий момент является единственным силовым фактором, а поперечные и нормальные силы отсутствуют, то такой изгиб называется чистым. В большинстве случаев в поперечных сечениях бруса наряду с изгибающими моментами возникают поперечные силы. В этом случае изгиб называют поперечным. Брус, работающий в основном на изгиб, называется балкой. На балку могут действовать сосредоточенные силы и моменты, а также распределенные по длине. Например, на рис. 2.17 F — сосредоточенная сила, М — сосредоточенный момент; на участке а приложена распределенная нагрузка от нуля до q max.
Анализ внутренних силовых факторов начинают с определения полной системы внешних сил. Рассмотрим некоторые характерные примеры и установим правила определения изгибающих моментов и поперечных сил. На рис. 2.18, а показана простейшая двухопорная балка, нагруженная силой F. Освобождаем балку от связей и заменяем их действие реакциями. Опора А представляет собой невесомый стержень, поэтому реакция RA пойдет вдоль него. В шарнире В реакцию раскладываем на две составляющие. Несмотря на то, что выбор системы координат, безусловно, произволен, в сопротивлении материалов принято ось z направлять вдоль бруса; оси х и у должны лежать в плоскости, перпендикулярной этой оси, причем поворот от оси х к оси у должен происходить против хода часовой стрелки, если смотреть с конца оси z (рис. 2.18, б). Начало отсчета располагают в центре тяжести поперечного сечения. В этом случае оси х и у будут главными центральными осями поперечного сечения.
Составим уравнения равновесия для плоской системы сил и определим неизвестные реакции связей. Неизвестных величин три — RA, YB, ZB. Уравнений статики тоже три, следовательно, задача статически определимая:
Отсюда находим реакции опор
Теперь приступим к выявлению внутренних силовых факторов в поперечных сечениях бруса. Для этого между точками приложения внешних сил и моментов, применяя метод сечений, мысленно разрезают балку на части (рис. 2.18, в и г) и составляют уравнения равновесия силовых факторов, приложенных к отсеченным частям. Так, в рассматриваемом примере необходимо делать сечения дважды: на расстоянии z 1 и z 2 от левой опоры. На рис. 2.18, в показано сечение бруса на расстоянии z 1 от левой опоры и проставлены внутренние силовые факторы: изгибающий момент М изг и поперечная сила Q. Следует обратить внимание на то, чтобы внутренние силовые факторы в поперечном сечении в левой и правой (см. рис. 2.18, г) частях были обязательно противоположны по направлению. Как уже известно, внутренние силовые факторы определяют из уравнений равновесия сил, приложенных к отсеченным частям. Следует условиться о знаках поперечных сил и моментов. Существует несколько способов определения знака изгибающего момента в поперечном сечении. 1. По знаку кривизны изогнутого бруса (рис. 2.19, а). Очевидно, знак будет зависеть от выбранной системы координат. Если ось у направить в противоположную сторону, то знаки М изг изменятся на противоположные.
2. Чаще всего при построении эпюр изгибающих моментов знак момента не зависит от выбранной системы отсчета, а ордината откладывается на сжатом волокне, т. е. в сторону вогнутости изогнутой оси бруса (рис. 2.19, б). 3. Если трудно представить, как будет выглядеть изогнутая ось бруса, то составляют сумму моментов нагрузок, действующих на левую отсеченную часть бруса. Если равнодействующий момент всех нагрузок, действующих на левую часть, будет направлен по часовой стрелке, то ордината изгибающего момента откладывается на эпюре вверх (т. е. изгибающий момент М изг в поперечном сечении действует против часовой стрелки и, следовательно, брус изгибается вогнутостью вверх — ордината будет отложена на сжатом волокне). Если же сумма моментов, действующих слева от сечения, направлена против часовой стрелки, то изгибающий момент на эпюре откладывается вниз (рис. 2.19, б). Для сил, лежащих справа от сечения, имеет место обратная зависимость. Правило определения знака для поперечных сил: если равнодействующая внешних сил, лежащих по левую сторону от сечения, направлена вверх, то поперечная сила в сечении считается положительной, а если вниз, то поперечная сила отрицательна. В сечении на расстоянии z 1 от начала координат, т. е. в левой части бруса от сечения (см. рис. 2.18, в), поперечная сила Q имеет положительный знак и на эпюре будет откладываться вверх. При рассмотрении равновесия правой отсеченной части для сил, лежащих справа от сечения, имеет место обратная зависимость. Чтобы легче усвоить правила определения знаков, желательно рассматривать равновесие, например, всегда левой части бруса. Дифференциальная зависимость между изгибающим моментом, поперечной силой и интенсивностью распределенной нагрузки. Правильность выбора знаков поперечных сил можно проверить, зная дифференциальную зависимость между изгибающим моментом и поперечной силой. Пусть брус, закрепленный произвольным образом, нагружен в общем случае распределенной нагрузкой интенсивности q = f (z) и находится в равновесии (рис. 2.20, а). Заданное направление для q — положительное. Выделим элемент бруса длиной dz и в сечениях приложим изгибающие моменты М и M + dM, а также поперечные силы Q и Q + dQ (рис. 2.20, б). Направления для этих силовых факторов приняты положительными в соответствии с обусловленным ранее правилом знаков. В пределах малого отрезка dz нагрузку q можно считать распределенной равномерно. Поскольку рассматриваем элемент бруса, находящегося в равновесии, то составим условия равновесия плоской системы сил: приравниваем к нулю сумму проекций всех сил на вертикальную ось и сумму моментов относительно точки С:
Откуда, отбросив величину высшего порядка малости qdz (dz /2), получим
Таким образом, поперечная сила представляет собой производную от изгибающего момента по длине бруса. Производная от поперечной силы дает интенсивность внешней распределенной нагрузки q. Из полученных дифференциальных зависимостей можно сделать некоторые общие выводы о характере эпюр изгибающих моментов и поперечных сил для прямого бруса. Если брус нагружен равномерно распределенной нагрузкой интенсивности q = const, очевидно, функция Q будет линейной, а М — квадратичной. Если брус нагружен сосредоточенными силами или моментами, а между точками их приложения интенсивность q = 0, то Q = const, a M является линейной функцией z. В точках приложения сосредоточенных сил эпюра Q претерпевает скачок на величину внешней силы, а в эпюре М возникает соответствующий излом (разрыв в производной). Построение эпюр изгибающих моментов и поперечных сил осуществляется в следующей последовательности: 1) определяют реакции опор; 2) выявляют в поперечных сечениях бруса все внутренние силовые факторы (их значение и знак); 3) строят эпюры. Построим эпюры для балки, представленной на рис. 2.18. 1. Определяем реакции опор. Составляем уравнения равновесия плоской системы сил:
2. Определяем внутренние изгибающие моменты в поперечных сечениях балки. Для этого рассматриваем равновесие отсеченной левой части (см. рис. 2.18, в): в сечении z 1
в сечении z 2
3. Определяем поперечные силы: в сечении z 1
Отсюда Q = RA = F (l - a)/ l; в сечении z 2
Отсюда Q = Fa / l. 4. Строим эпюры изгибающих моментов. Эпюра М изг в пределах 0 £ z 1 £ а имеет линейную зависимость. Задаемся z 1 = 0, при этом М изг = 0. Откладываем эту точку на эпюре (рис. 2.21). Далее при z 1 = а M изг = = F (l - a) a / l.
В пределах а £ z 2 £ l получаем: при z 2 = а M изг = F (l - a) a / l; при z 2 = l М изг = 0. Откладываем эти ординаты (они построены на сжатом волокне) и соединяем линиями. Следует заметить, что на втором участке можно было ординаты не вычислять, так как в шарнирной опоре В момент не может возникать, и поэтому на эпюре нужно сразу отложить 0. 5. Строим эпюры поперечных сил. Как было определено в п. 3, поперечные силы постоянны на каждом из двух участков, поэтому откладываем подсчитанные значения с учетом знаков. Нужно обратить внимание, что в точке приложения внешней силы должен быть скачок, равный приложенной силе. Кроме того, можно проверить правильность установленных знаков поперечных сил. Тангенс угла наклона линии М изг на эпюре изгибающих моментов показывает на знак поперечной силы. Если угол острый, то тангенс положительный (производная dM / dt > 0), а следовательно, и поперечная сила имеет знак «+». Если угол наклона линии с осью z тупой, то поперечная сила отрицательная. Сопоставьте построенные эпюры М изг и Q (см. рис. 2.21).
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Последнее изменение этой страницы: 2021-01-08; просмотров: 564; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.151.106 (0.119 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
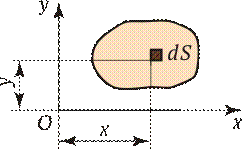Рис. 2.11
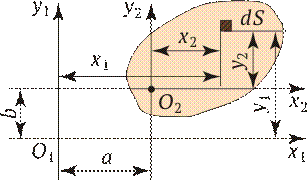Рис. 2.12
Рис. 2.13
Рис. 2.14
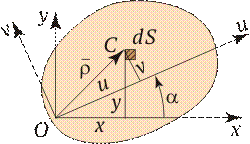Рис. 2.15
Рис. 2.16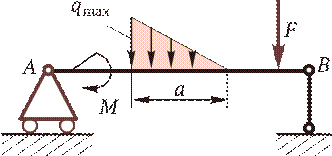
Рис. 2.17
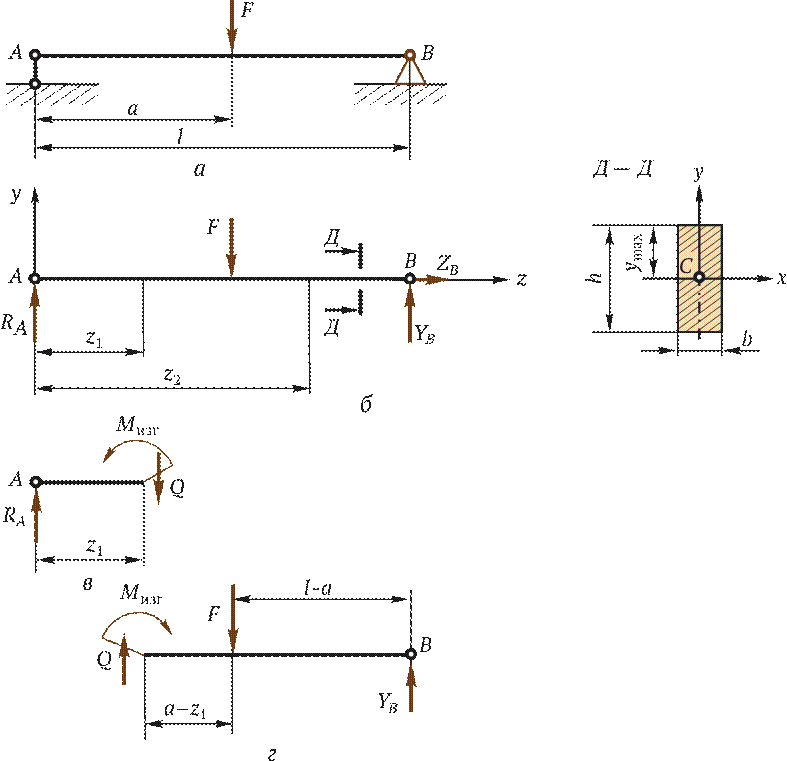Рис. 2.18
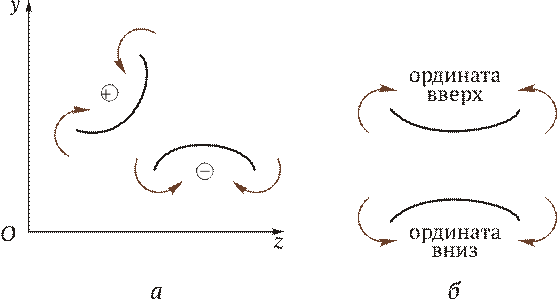Рис. 2.19
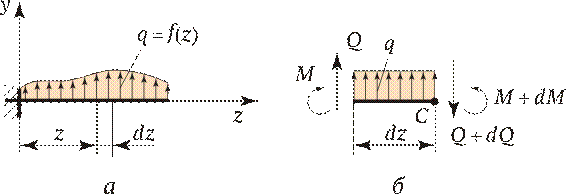Рис. 2.20
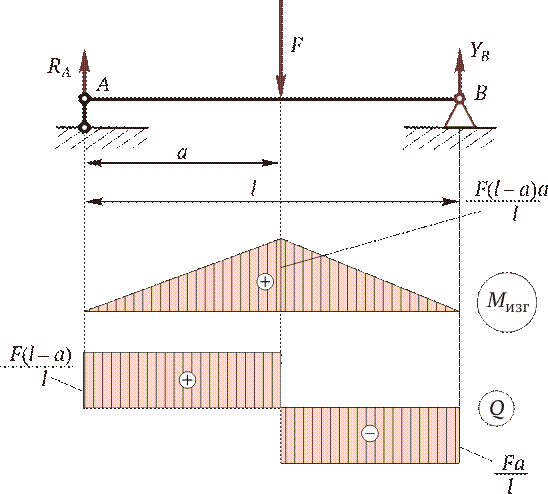Рис. 2.21
