
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифференциальные уравнения порядка n. ⇐ ПредыдущаяСтр 4 из 4
Общий вид: Если уравнение сведено к виду Методы понижения порядка. Случай 1. Если в уравнении отсутствуют младшие порядки производных. Так, в уравнении Докажем, что в этом случае понизится на
Пример 335. Решить уравнение 2 порядка Замена: Уравнение сводится к виду
Вспомним о том, что
Задача 336. Решить дифференциальное уравнение Решение. Это уравнение сводится к
Особые решения: Далее, Провести обратную замену здесь означает вычислить первообразную, ведь у нас было
Ответ.
Задача 337. Найти общее решение уравнения Решение. Сделаем замену Тогда уравнение сведено к виду
Теперь вспомним, что было
Особые решения: А теперь конкретизируем константы с помщью условий Коши, то есть найдём частное решение. У нас есть информация:
а также Тогда
Ответ. Задача 338. Найти общее решение уравнения Решение. Сделаем замену решаем его: Теперь вспомним, что
Особые решения:
Уравнение 3 порядка, и здесь получилось 3 константы. Теперь найдём частное решение. В первом столбце та или иная производная, во втором - что в неё подставить, какое из условий Коши. В третьем-что при этом получится. Везде подставляем
Это система из 3 уравнений, но только метод Гаусса в полном объёме здесь не нужен, потому что сразу определено Ответ. Общее реш. Случай 2. Если в уравнении содержится Например, В этом случае замена Естественно возникает вопрос: а существуют ли в принципе такие преобразования, не содержат ли они противоречия? Всегда ли можно выразить Пример 1. Пример 2. Как видите,
Итак, замена Получается
вычисляем производную произведения двух сомножителей, причём в каждом из них ещё и композиция:
учитывая, что 1-я производная от 2-я производная от
Таким образом, доказали, что порядок при таком преобразовании обязательно понизится на 1 единицу. Доказали, что замена
Пример 339: Это уравнение колебательного процесса: чем больше координата, тем больше действует сила (ускорение) в противоположную сторону. После замены, уравнение преобразуется к виду: Сначала 1-й шаг: ищем неизвестную функцию
2 шаг. Обратная замена.
На этом примере увидели, что уравнение
|
|||||||||||||||
|
Последнее изменение этой страницы: 2021-01-08; просмотров: 54; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.23.130 (0.033 с.) |
 .
. то оно называется разрешённым относительно старшей (высшей) производной.
то оно называется разрешённым относительно старшей (высшей) производной. отсутствуют все производные до порядка
отсутствуют все производные до порядка  , в том числе 0-го порядка, а именно сама функция
, в том числе 0-го порядка, а именно сама функция  , и начинаются с порядка
, и начинаются с порядка  . В этом случае можно сделать замену
. В этом случае можно сделать замену  , то есть в качестве новой функции взять производную самого младшего порядка, которая есть в уравнении.
, то есть в качестве новой функции взять производную самого младшего порядка, которая есть в уравнении. .
.

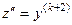 и так далее. Таким образом, замена
и так далее. Таким образом, замена  .
. , тогда
, тогда 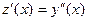 .
.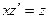 . Для
. Для 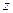 уравнение 1 порядка и решается обычными методами, изученными ранее.
уравнение 1 порядка и решается обычными методами, изученными ранее.


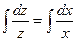
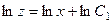
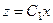 .
. , то есть теперь, чтобы сделать обратную замену и восстановить
, то есть теперь, чтобы сделать обратную замену и восстановить 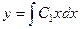 =
= 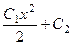 . В общем решении здесь не одна, а две константы, вторая появляется из-за того, что интегрировали для обратной замены. А если уравнение 3 порядка, то будет 3 константы в общем решении.
. В общем решении здесь не одна, а две константы, вторая появляется из-за того, что интегрировали для обратной замены. А если уравнение 3 порядка, то будет 3 константы в общем решении. .
. заменой
заменой  .
.
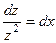

 .
.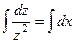
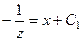
 .
. =
= 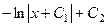 .
.  .
. 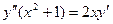 и частное решение при условиях Коши:
и частное решение при условиях Коши:  .
.  , тогда
, тогда 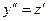 .
. 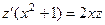 .
.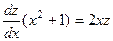

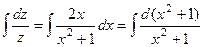

 .
. =
= 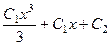 - это общее решение.
- это общее решение. остаётся только
остаётся только  .
. ,
, 
 ,
,  , то есть
, то есть . Тогда частное решение:
. Тогда частное решение:  .
. и частное решение при условиях Коши:
и частное решение при условиях Коши:  .
.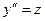 , тогда уравнение сводится к
, тогда уравнение сводится к 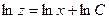
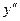 , и сделаем обратную замену, для этого надо 2 раза перейти к первообразной.
, и сделаем обратную замену, для этого надо 2 раза перейти к первообразной.
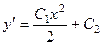
 .
.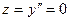
 , впрочем, они входят в состав общего решения, ведь при
, впрочем, они входят в состав общего решения, ведь при 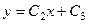 .
. .
.
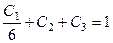




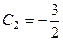 , подставляем в первое
, подставляем в первое 
 . Итак,
. Итак,  .
.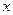 . Тип уравнения такой:
. Тип уравнения такой: 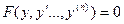 .
.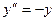 - уравнение колебательного процесса в физике.
- уравнение колебательного процесса в физике.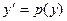 , то есть
, то есть  - в роли функции от
- в роли функции от  ,
,  . Выразим
. Выразим 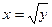 , и подставим в производную, тогда верно, что
, и подставим в производную, тогда верно, что 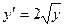 .
. ,
, 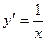 . Тогда
. Тогда  , и в итоге
, и в итоге  .
.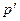 , потому что фактически здесь была композиция:
, потому что фактически здесь была композиция:  , и следующую производную от неё надо вычислять именно как для композиции.
, и следующую производную от неё надо вычислять именно как для композиции. .
. 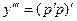 =
= 
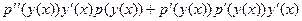
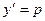 , получится
, получится 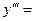
 .
. ,
,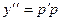
 .
.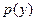 .
.

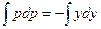
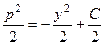
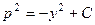 .При этом
.При этом 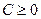 , иначе справа всё выражение было бы отрицательно и не могло бы быть равно
, иначе справа всё выражение было бы отрицательно и не могло бы быть равно  . Если
. Если  . Итак,
. Итак,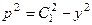 , то есть
, то есть  . Итак, мы нашли неизвестную функцию
. Итак, мы нашли неизвестную функцию  , то есть теперь надо решить уравнение:
, то есть теперь надо решить уравнение:  .
.


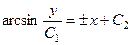

 . Здесь
. Здесь  называется амплитудой колебаний,
называется амплитудой колебаний, 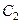 - фазой. Впрочем, при
- фазой. Впрочем, при  получается не синус, косинус, а именно, по формуле приведения
получается не синус, косинус, а именно, по формуле приведения  . Поэтому в решении есть и косинусы. Более того, мы могли при решении знак плюс-минус также перенести,
. Поэтому в решении есть и косинусы. Более того, мы могли при решении знак плюс-минус также перенести,  , тогда бы слева сразу получалось 2 варианта: или арксинус, или арккосинус.
, тогда бы слева сразу получалось 2 варианта: или арксинус, или арккосинус.


