
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Частное решение. Задача Коши.
Если задать точку Примечание. Движение в физике задаётся с помощью уравнений со 2-й производной (ускорение), в общем решении две константы, поэтому там требуются 2 условия (начальная координата и начальная скорость), чтобы определить траекторию. Задача 320. Решить уравнение Решение. Запишем Ответ. Проверка: Практика 29. Поле направлений. Если задано дифференциальное уравнение Задача 321. Решить дифференциальное уравнение Заметим, что тангенс угла наклона касательной для любого решения здесь равен
Можно предположить, что решения это прямые вида
Далее, В итоге, общее решение Проверка. Задача 322. Решить уравнение Решение. Ответ.
Задача 323. Решить дифференциальное уравнение
Решение. Итак, Но выразим явно функцию Проверка: Теперь применим условие Коши Теперь возвращаемся к общему решению, но там уже фиксируем найденное Ответ. Общее решение Задача 324. Решить уравнение Решение. Особое решение
Ответ. Задача 325. Решить уравнение
Решение.
Ответ.
Задача 326. Решить уравнение
Решение.
Ответ.
Однородные уравнения. Далеко не все уравнения - с разделяющимися переменными. Так, если присутствует множитель Уравнения, сводящиеся к виду Замена
Тогда
Таким образом, свели к уравнению с разделяющимися переменными.
Задача 327. Решить дифференциальное уравнение Решение. Оно было ранее решено как «с разделяющимися переменными», но оно также является и однородным, можно на его примере отработать алгоритм действий с однородными. Сделаем замену Задача 328. Решить уравнение Решение. Уравнение можно рассматривать как «однородное», то есть вида Сделаем замену надо сделать обратную замену,
Ответ. Линейные уравнения. Уравнение вида Если При этом, Во-первых, заметим, что линейные однородные уравнения фактически являются уравнениями с разделяющимися переменными. Действительно, Задача 329. Решить уравнение Решение. Линейное однородное фактически является уравнением с разделяющимися переменными.
Ответ. Проверка:
Линейные неоднородные уравнения. Метод Лагранжа (метод вариации произвольной постоянной). Задача 330. Решить линейное уравнение 1 шаг. Решаем соответствующее однородное уравнение. 2 шаг. Методом Лагранжа решаем неоднородное. Ищем решение в виде:
Тогда Теперь подставим это в
Общее решение неоднородного состоит из двух слагаемых: частное решение неоднородного (его мы и искали на 2-м шаге методом Лагранжа) и общее решение однородного, которое нашли на 1-м шаге, и оно воспроизвелось само в конце 2-го шага. Это происходит из-за того, что Проверка. Можно подставить частное решение неоднородного, и это слагаемое само по себе тоже является решением: Выполняется ли
Задача 331. Решить линейное неоднородное уравнение Решение. 1) Решим соответствующее однородное.
2) Ищем общее решение неоднородного в виде
Ответ. Здесь частное решение неоднородного это Задача домашняя (разобрать самостоятельно). Решить линейное неоднородное уравнение Решение. 1) Сначала решим однородное
2) Ищем решение неоднородного в виде При этом Подставляем
Тогда
Уравнения Бернулли. Уравнение вида Отличаются от линейных только наличием Если n=0 получается линейное неоднородное Если n=1 то ещё лучше, получается однородное: то есть При
Алгоритм решения. 1) Разделить на 2) Сделать замену 3) решить линейное (в 2 шага, сначала однородное, потом неоднородное) 4) сделать обратную замену: так как
Докажем, что уравнение Бернулли сводится к линейному.
Тогда уравнение
Это уже линейное неоднородное уравнение. Задача 332. Решить дифференциальное уравнение Решение. 1) Разделим на 2) Введём замену Тогда
Оно решается в 2 шага: сначала соответствующее однородное. 3.1)
3.2) Метод Лагранжа. Ищем решение неоднородного в виде:
Тогда 4) Обратная замена: вспомним, что Ответ. Уравнения в полных дифференциалах. Рассмотрим ещё один метод решения дифференциальных уравнений, основанный на использовании потенциала поля. Пусть дано дифференциальное уравнение вида причем Задача 333. Решить дифференциальное уравнение Решение. Проверяем тип уравнения. Здесь
Ищем потенциал. Соединяем точки (0,0) и
Тогда
Задача 334. Решить дифференциальное уравнение
Решение. Проверяем тип уравнения. Здесь При этом
|
|||||||
|
Последнее изменение этой страницы: 2021-01-08; просмотров: 71; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.192.3 (0.122 с.) |
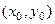 и найти кривую (одну из бесконечного множества), проходящую через неё, то есть
и найти кривую (одну из бесконечного множества), проходящую через неё, то есть 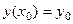 , то можно определить значение параметра
, то можно определить значение параметра 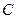 . Это дополнительное условие называется условием Коши. Чтобы найти эту одну кривую, надо подставить
. Это дополнительное условие называется условием Коши. Чтобы найти эту одну кривую, надо подставить  , то есть кривая проходит через точку
, то есть кривая проходит через точку  запишется в виде
запишется в виде  , тогда
, тогда 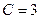 . Функция
. Функция 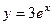 называется частным решением.
называется частным решением. .
.  . Теперь домножим на dx, разделим на
. Теперь домножим на dx, разделим на  .
.  . Особое решение
. Особое решение  . Далее,
. Далее, 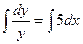

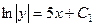
 =
=  (где C > 0 так как
(где C > 0 так как  ). Но нам надо выразить не
). Но нам надо выразить не  , а само
, а само 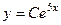 , где
, где 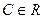 .
. ,
,  , то это означает, что в каждой точке некоторой области D задано направление касательной, т.е. под каким углом наклона там пройдёт кривая. Ведь
, то это означает, что в каждой точке некоторой области D задано направление касательной, т.е. под каким углом наклона там пройдёт кривая. Ведь  это тангенс угла наклона производной, и он дан для каждой точки, а именно равен
это тангенс угла наклона производной, и он дан для каждой точки, а именно равен  . Возникает так называемое «поле направлений». Иногда даже зрительно можно заранее предположить, какие кривые являются решениями дифф. уравнения. Увидим это на следующем примере.
. Возникает так называемое «поле направлений». Иногда даже зрительно можно заранее предположить, какие кривые являются решениями дифф. уравнения. Увидим это на следующем примере. .
.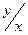 , то есть касательные направлены радиально от центра.
, то есть касательные направлены радиально от центра.
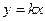 . А теперь решим задачу аналитически.
. А теперь решим задачу аналитически.



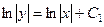 . Кстати, любую константу можно задать в виде
. Кстати, любую константу можно задать в виде  , так как область значений логарифма
, так как область значений логарифма  . Для удобства сразу запишем
. Для удобства сразу запишем  , чтобы логарифмировать это выражение. Впрочем, это не обязательно делать именно так,
, чтобы логарифмировать это выражение. Впрочем, это не обязательно делать именно так, 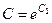 можно преобразовать и позже.
можно преобразовать и позже. 
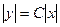 .
.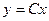 . Ответ.
. Ответ.  , подставим в уравнение
, подставим в уравнение 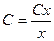 .
. .
.
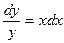
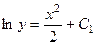
 , где
, где 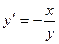 , и найти частное решение, удовлетворяющее условию Коши
, и найти частное решение, удовлетворяющее условию Коши  .
.
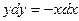

 , умножим на 2:
, умножим на 2: 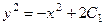 . Константа
. Константа 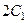 не может быть отрицательной, иначе
не может быть отрицательной, иначе  и не будет существовать корень квадратный. Тогда
и не будет существовать корень квадратный. Тогда  , и можно обозначить её в виде
, и можно обозначить её в виде  .
. , это уравнение окружности.
, это уравнение окружности. :
:  общее решение.
общее решение. .
. ,
,  тогда в уравнении остаётся всего одно неизвестное, а именно
тогда в уравнении остаётся всего одно неизвестное, а именно 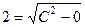
 , т.е.
, т.е.  .
. .
.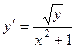 .
.
 .
.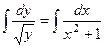

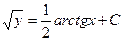
 .
.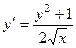 .
.
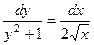
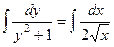

 .
.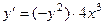 .
.



 .
. , то что бы ни выносили за скобку, всё равно там останутся обе переменные, а не одна:
, то что бы ни выносили за скобку, всё равно там останутся обе переменные, а не одна:  или
или  .
.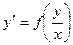 называются однородными (по степени). Примечание. Не путать: название «однородные» будет использоваться ещё и для других свойств, например, когда правая часть линейного уравнения равна 0.
называются однородными (по степени). Примечание. Не путать: название «однородные» будет использоваться ещё и для других свойств, например, когда правая часть линейного уравнения равна 0. 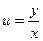 сводит однородное уравнение к уравнению с разделяющимися переменными.
сводит однородное уравнение к уравнению с разделяющимися переменными.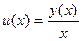
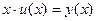 , тогда
, тогда  =
= 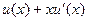 .
. , далее
, далее


 . Тогда
. Тогда  , то есть
, то есть  . Тогда
. Тогда 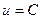 . Сделаем обратную замену. Если
. Сделаем обратную замену. Если  , из чего следует, что общее решение
, из чего следует, что общее решение  .
.  .
. . Тогда уравнение приводится к виду
. Тогда уравнение приводится к виду  , то есть
, то есть 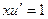
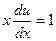

 .
.
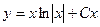 .
. называется линейным.
называется линейным.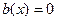 , то оно называется линейным однородным.
, то оно называется линейным однородным. не может быть тождественно равно 0, иначе вообще нет слагаемого с производной
не может быть тождественно равно 0, иначе вообще нет слагаемого с производной  , то есть уравнение не являлось бы дифференциальным. Но тогда можно поделить всё уравнение на
, то есть уравнение не являлось бы дифференциальным. Но тогда можно поделить всё уравнение на  .
.
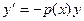
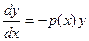
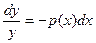
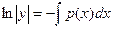 , где
, где  первообразная, с точностью до константы. В итоге,
первообразная, с точностью до константы. В итоге, 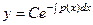 , то есть общее решение линейного однородного уравнения имеет вид: константа, умноженная на экспоненту в степени первообразной от коэффициента
, то есть общее решение линейного однородного уравнения имеет вид: константа, умноженная на экспоненту в степени первообразной от коэффициента 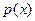 , взятую с другим знаком.
, взятую с другим знаком.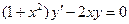 .
.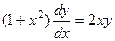


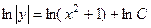
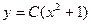 .
.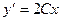 , подставим в исходное уравнение, будет
, подставим в исходное уравнение, будет 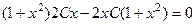
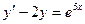 .
.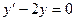 .
. 


 - общее решение однородного.
- общее решение однородного.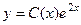 . Ищем производную:
. Ищем производную: =
=  . Всё это подставим в неоднородное:
. Всё это подставим в неоднородное:
 , тогда
, тогда 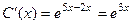 .
. =
= 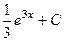 .
.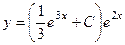 =
= 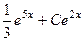 .
.  всегда ищется с помощью её производной, а значит, в ней присутствует слагаемое
всегда ищется с помощью её производной, а значит, в ней присутствует слагаемое  .
. =
= 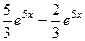 =
=  . Верно.
. Верно. .
. 


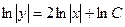
 - общее решение однородного уравнения.
- общее решение однородного уравнения.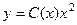 , при этом получится
, при этом получится 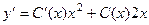 , подставляя
, подставляя 
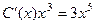
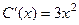
 . Тогда
. Тогда  т.е.
т.е. 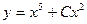 .
. 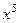 . Кстати, можно сделать и проверку этого ответа:
. Кстати, можно сделать и проверку этого ответа:  .
.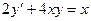 .
.  .
.

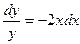
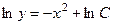
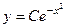 .
. .
. .
.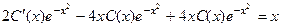




 .
. =
=  . Ответ.
. Ответ.  .
.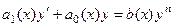 называется уравнением Бернулли. Так как коэффициент
называется уравнением Бернулли. Так как коэффициент  .
. в правой части.
в правой части.
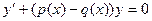 .
. ,
, 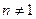 получается уже собственно, уравнение Бернулли. Оно является обобщением линейного уравнения.
получается уже собственно, уравнение Бернулли. Оно является обобщением линейного уравнения.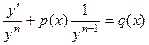 .
.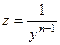 . Тогда оно сведётся к линейному по
. Тогда оно сведётся к линейному по 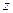 .
. .
. , тогда
, тогда  по правилам дифференцирования композиции. Получили, что
по правилам дифференцирования композиции. Получили, что  .
.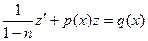 , или
, или  .
.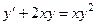 .
.  . Получаем
. Получаем  .
.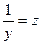 , при этом
, при этом 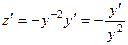 .
. . Для удобства умножим ещё на
. Для удобства умножим ещё на  .
. . Это линейное неоднородное уравнение.
. Это линейное неоднородное уравнение.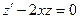 . Однородное является уравнением с разделяющимися переменными.
. Однородное является уравнением с разделяющимися переменными. 



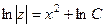
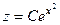 это общее решение однородного уравнения.
это общее решение однородного уравнения.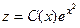 . Тогда
. Тогда  . Подставим эти выражения в неоднородное уравнение
. Подставим эти выражения в неоднородное уравнение 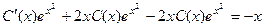



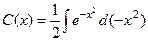
 .
. 
 .
.
 .
.  ,
, . Тогда это уравнение называется «уравнением в полных дифференциалах». Здесь
. Тогда это уравнение называется «уравнением в полных дифференциалах». Здесь  является потенциальным векторным полем. В этом случае уравнение можно представить в виде
является потенциальным векторным полем. В этом случае уравнение можно представить в виде 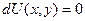 , а значит,
, а значит,  . Затем остаётся только выразить
. Затем остаётся только выразить 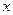 .
.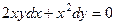 .
.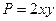 ,
,  . При этом
. При этом ,
,  . То есть, векторное поле
. То есть, векторное поле  потенциально.
потенциально.
 с помощью ломаной, и вычисляем:
с помощью ломаной, и вычисляем: =
=  =
=  . Итак,
. Итак,  .
. общее решение. Ответ.
общее решение. Ответ. 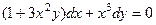 .
. ,
,  .
. ,
,  . То есть, векторное поле потенциально. Ищем потенциал. Соединяем точки (0,0) и
. То есть, векторное поле потенциально. Ищем потенциал. Соединяем точки (0,0) и  =
= 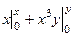 =
=  . Итак,
. Итак, 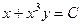 . Тогда
. Тогда  общее решение уравнения. Ответ.
общее решение уравнения. Ответ. 


