
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Подведение под знак дифференциала.Стр 1 из 4Следующая ⇒
Практика 26. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ. Определение. Если Свойство. Если Определение. Множество всех первообразных от одной и той же функции
Таблица основных интегралов.
Методы интегрирования. 1. Преобразования подынтегральных выражений. Пример. Пример. Задача 277. Вычислить Решение. Известно, что
Ответ. Задача 278. Вычислить Решение. Замечая, что
Ответ. Задача 279. Вычислить интеграл Решение. Воспользуемся формулой понижения степени, чтобы перейти от степеней тригонометрических функций к выражениям типа
Ответ. Задача 279-Б. Вычислить Решение. Применим формулу понижения степени.
Задача 280. Вычислить Решение. Сначала нужно выделить целую часть дроби и отделить правильную дробь.
Ответ. Задача 281. Вычислить Решение. В данном случае неправильная дробь, причём степень в числителе более высокая. Можно применить общий метод выделения целой части, то есть поделить числитель на знаменатель.
Теперь, когда свели к сумме табличных интегралов, получаем ответ: Ответ. Задача 282. Вычислить Решение. D < 0, можно выделить полный квадрат:
С помощью замены
Ответ. Задача 283. Вычислить Решение. В предыдущей задаче было D<0, а в этой D=0. Выделяя полный квадрат, получим В этом случае сводится не к арктангенсу, а к степенной функции,
Задача 284. Вычислить Решение.
Для того, чтобы применить формулу, нужно обозначить
Теперь интеграл имеет вид После обратной замены получаем ответ. Ответ.
Задача 285. Вычислить Решение. Здесь можно было бы применить формулу для косинуса двойного угла, но это преобразование бы только увеличило степени. Поэтому в данном случае для удобнее применить формулу понижения степени ко второму множителю и не менять первый.
= Первый интеграл вычисляется уже известным способом, а во втором снова понизим степень.
Ответ.
Замена переменной. Задача 286. Вычислить Решение. Сделаем замену
Обратная замена: Более того, область определения исходной функции
Если в функции присутствуют корни разного порядка, например Если Объяснение, почему все корни выразятся через целые степени
Задача 287. Вычислить интеграл Решение. НОК (2,3,5) = 30. Поэтому замена Тогда Другие корни пересчитываются аналогично:
Надо ещё пересчитать дифференциал для новой переменной
Теперь подставим всё это в интеграл.
= Ответ.
Практика 27. Задача 294. Вычислить интеграл Решение.
Ответ. Задача 295. Вычислить Решение. Ответ. Задача 296. Вычислить Решение. Если сразу подвести под знак дифференциала то, что есть в числителе, то будет
и теперь, после замены Далее, сделаем преобразование, которое позволит оставить только однотипные корни:
далее уже с помощью обычных действий со степенными функциями:
После обратной замены получаем ответ, при этом также заодно обратно меняем дробные степени на корни. Ответ. Задача 297. Вычислить Решение. =
Ответ. Задача 298. Вычислить Решение. Заметим, что в числителе производная того выражения, которое есть в знаменателе. Тогда Здесь фактически мы применили замену Ответ.
Задача 299. Вычислить Решение. Здесь, в отличие от прошлой задачи, в числителе уже произвольный многочлен, не соответствующий производной от знаменателя. Тем не менее, можно путём арифметических операций получить там дифференциал знаменателя: Домножим и поделим на 2, чтобы исправился коэффициент при
Теперь осталось прибавить и отнять 2, и будет получено
= В первом слагаемом делается ровно то же самое, что в прошлой задаче, а во втором - выделить полный квадрат, и в итоге сводится к арктангенсу:
Ответ.
Задача 300. Вычислить интеграл Решение. В отличие от прошлой задачи, здесь не надо прибавлять и вычитать, так как полный дифференциал знаменателя это Далее, Ответ.
Интегрирование по частям.
Задача 301. Вычислить Решение. Если обозначить Составим таблицу:
Задача 302. Вычислить Решение. Пусть
Тогда Ответ. Задача 303. Вычислить интеграл Решение.
Ответ.
А есть такие случаи, когда функция состоит не из 2 множителей, а всего из одного, но мы ведь всё равно можем считать, что второй множитель есть, только он равен 1. Задача 304.
Здесь производная от подынтегральной функции устроена лучше и проще, чем сама функция, но правда, пришлось допустить некоторое незначительное усложнение типа функции при переходе от
Задача 305. Вычислить интеграл Решение. Пусть
Построим таблицу:
Тогда
Ответ.
Задача 306. Вычислить интеграл Решение. Производная арктангенса это рациональная дробь. И это мы используем, обозначая её
Тогда: Второе слагаемое далее уже решается подведением под знак dx.
Интегралы Задача 307. Вычислим интеграл На первом шаге, обозначаем
На 2-м шаге, в том интеграле, который получился, обозначим аналогичным образом:
Получается Из равенства
Ответ.
Домашние задачи. Практика 28 (530 гр). Задача 312. Вычислить интеграл Решение. В данном случае знаменатель уже разложен в произведение множителей первой степени. Теперь представим дробь в виде суммы:
После приведения к общему знаменателю:
Тогда Перегруппируем слагаемые, так, чтобы вынести отдельно вторые степени, первые степени и константы.
Отсюда строим систему уравнений:
Сначала ко 2-й строке прибавили 1-ю, умноженную на 5, затем от 3-й отняли 1-ю, умноженную на 6. Так мы обнулили всё ниже углового элемента А теперь к 3-й строке прибавили 2-ю, умноженную на 3:
Уже получилась треугольная основная матрица. Ей соответствует такая система:
Теперь интеграл сводится к такому виду:
Ответ. Задача 313. Вычислить интеграл Решение. Сначала разложим знаменатель на множители:
Ответ. Задача (домашняя). Вычислить интеграл Кратко:
Ответ.
Случай 2. Если все корни
Задача 314. Вычислить интеграл Решение. Наличие множителя Сначала извлечём дробь из интеграла, и ищем разложение в виде:
Приводим к общему знаменателю.
Так как знаменатели равны, то осталось приравнять числители.
Тогда надо приравнять коэффициенты при каждой степени, получится То есть система уравнений на поиск трёх неопределённых коэффициентов:
Тогда исходный интеграл распадается на сумму:
= Задача 315. Вычислить интеграл Решение. Как видим, здесь корень 1 имеет кратность 2. Разложение на простейшие дроби нельзя проводить так, как будто бы здесь три независимых множителя
Приведём к общему знаменателю:
Числитель этой дроби равен числителю исходной, той, которая была в интеграле:
Система приведена к виду: Тогда В 1 и 3 слагаемых - как раньше, а вот во 2-м логарифм в ответе не получится, ведь тут уже 2-я а не 1-я степень в знаменателе. Полезно вспомнить, что То есть, интеграл от -2 степени будет содержать -1 степень, и меняется знак. Ответ.
Задача 316. Вычислить интеграл Решение. Здесь корень 0 имеет кратность 2, остальные корни простые.
После приведения к общему знаменателю, числитель будет такой:
После приведения подобных:
то матрицу 4 порядка для метода Гаусса строить не надо, а останется только маленькая система на C,D.
Ответ.
Случай 3. Если есть комплексные корни (не все корни Множители 2 степени типа Задача 317. Вычислить интеграл Решение. Ищем разложение в виде:
Получаем систему:
В то же время, Итак, заменим в интеграле «большую» дробь на сумму маленьких, каждая из которых приводится к табличному интегралу.
Итак, мы рассмотрели все типы рациональных дробей. Других случаев нет, т.к. неделимых множителей 3-й степени уже быть не может, для многочлена 3 степени есть хотя бы один действительный корень. Задача 318. Вычислить интеграл Решение. Запишем разложение на простейшие дроби: Это равно Тогда
Тогда Во втором слагаемом, можно подвести под знак дифференциала:
Ответ. «ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ» Практика 29. Поле направлений. Если задано дифференциальное уравне
|
|||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-01-08; просмотров: 253; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.139.50 (0.206 с.) |
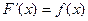 , то
, то  называется первообразной от функции
называется первообразной от функции 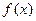 .
.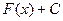 (для любого
(для любого 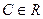 ) тоже является первообразной для той же самой функции
) тоже является первообразной для той же самой функции 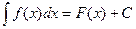 .
.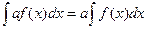 2.
2. 
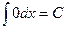
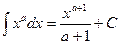 (
(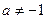 )
)


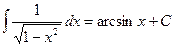

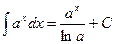

 ;
; 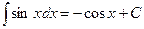
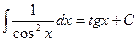

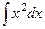 =
= 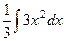 =
= 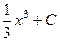 .
.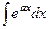 =
=  =
= 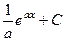 .
.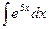 .
.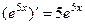 . При дифференцровании функций вида
. При дифференцровании функций вида 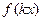 происходило умножение на константу, а при интегрировании наоборот, деление. Чтобы понять, почему это так, постараемся сначала сформировать внутри интеграла готовую производную от этой экспоненты, для чего домножим и поделим на 5.
происходило умножение на константу, а при интегрировании наоборот, деление. Чтобы понять, почему это так, постараемся сначала сформировать внутри интеграла готовую производную от этой экспоненты, для чего домножим и поделим на 5. =
= 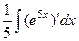 =
=  .
.  .
.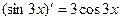 , преобразуем так:
, преобразуем так: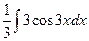 =
= 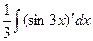 =
= 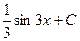 .
. .
.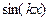 или
или 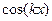 .
. =
=  =
= 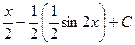 .
.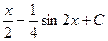 .
.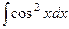 .
. =
=  =
= =
= 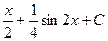 .
.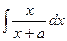 .
. 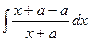 =
=  =
= теперь, когда разбили на сумму или разность табличных интегралов, получаем ответ:
теперь, когда разбили на сумму или разность табличных интегралов, получаем ответ: 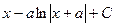 .
.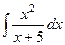 .
. =
= 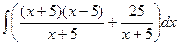 что тоже приводит к
что тоже приводит к 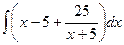 .
. .
.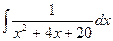 .
.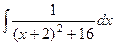 =
=  .
. сводится к интегралу:
сводится к интегралу:  =
= 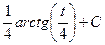 , и далее с помощью обратной замены получаем ответ.
, и далее с помощью обратной замены получаем ответ.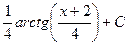 .
.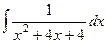 .
. .
.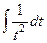 =
= 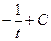 =
= 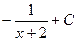 . Ответ.
. Ответ. 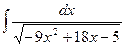 .
.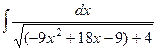 =
= 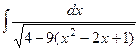 =
=  =
= 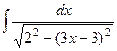 .
. . Но сначала сделаем так, чтобы и в числителе оказался не просто
. Но сначала сделаем так, чтобы и в числителе оказался не просто  а
а 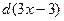 :
: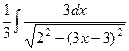 =
=  .
.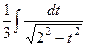 , и равен
, и равен 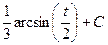 .
.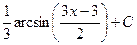 .
.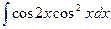 .
.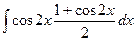 =
= 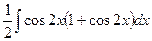 =
=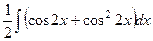 =
= 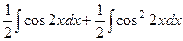 .
. =
=  =
= 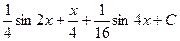 .
.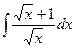 .
. , тогда
, тогда  ,
, 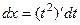 ,
,  .
. =
= 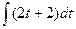 =
=  .
.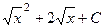 =
= 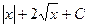 .
. из-за наличия в ней квадратного корня, точка 0 не входит в область определения, так как корень там и в знаменателе, так что знак модуля в ответе является излишним, ответ можно записать так:
из-за наличия в ней квадратного корня, точка 0 не входит в область определения, так как корень там и в знаменателе, так что знак модуля в ответе является излишним, ответ можно записать так: 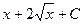 .
.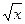 и
и 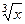 , то замена должна происходить через корень порядка НОК (наименьшее общее кратное). Причина в том, что именно при этом все корни переводятся в целые степени от
, то замена должна происходить через корень порядка НОК (наименьшее общее кратное). Причина в том, что именно при этом все корни переводятся в целые степени от  .
.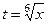 , тогда:
, тогда:  ,
, 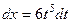 .
.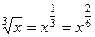 =
=  ,
,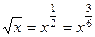 =
=  .
.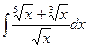 .
.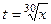 .
. . Дополняющий множитель до НОК для числа 5 как раз и есть 6, ведь НОК = 30.
. Дополняющий множитель до НОК для числа 5 как раз и есть 6, ведь НОК = 30.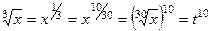 ,
, 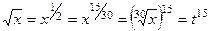 .
.

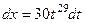 .
. =
= 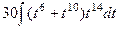 =
=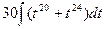 =
= 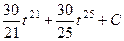 , и после обратной замены:
, и после обратной замены: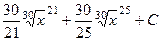 .
.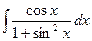 .
. 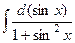 =
= 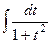 =
= 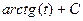 =
= .
. 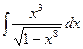 .
.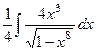 =
=  =
= 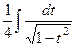 =
= 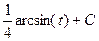 =
= 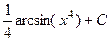 .
.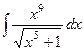 .
. , но тогда в знаменателе получится выражение
, но тогда в знаменателе получится выражение 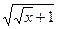 . чтобы не происходило такого усложнения и не появились вложенные квадратные корни, надо подводить не весь числитель, а отделить тот множитель, который нам удобнее, чтобы потом всё выражалось через
. чтобы не происходило такого усложнения и не появились вложенные квадратные корни, надо подводить не весь числитель, а отделить тот множитель, который нам удобнее, чтобы потом всё выражалось через 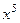 .
.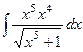 =
=  =
= 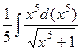
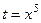 , получится
, получится 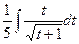 .
. =
= 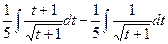 =
=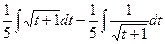 =
= 
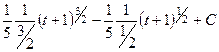 =
=  .
.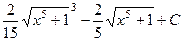 .
.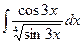 .
.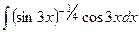 =
=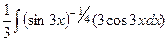 =
= 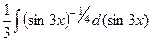 =
= 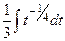 =
=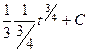 =
= 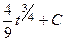 =
= 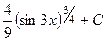 .
. .
. .
. 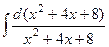 =
=  =
= 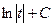 =
= 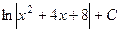 .
. для упрощения выражения. Кстати, выделение полного квадрата в знаменателе это здесь был бы тупиковый путь, ведь в числителе не константа а многочлен, то есть не удалось бы свести к виду
для упрощения выражения. Кстати, выделение полного квадрата в знаменателе это здесь был бы тупиковый путь, ведь в числителе не константа а многочлен, то есть не удалось бы свести к виду 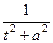 .
. .
. 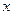 :
: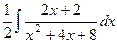
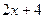 :
: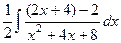 =
= .
.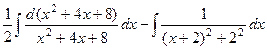 =
=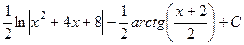 .
. .
.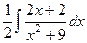 =
= 
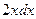 , в знаменателе нет 1-й степени, а его производная поэтому не содержит константу.
, в знаменателе нет 1-й степени, а его производная поэтому не содержит константу. =
= 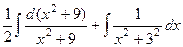 , и в итоге:
, и в итоге: .
.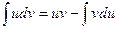
 .
.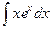 .
. 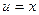 ,
, 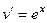 , то при переходе к
, то при переходе к 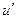 степенной понизится степень, в данном случае она вообще перейдёт в 1. А вот для второго множителя переходим к первообразной, но там не усложняется, остаётся точно так же как и было,
степенной понизится степень, в данном случае она вообще перейдёт в 1. А вот для второго множителя переходим к первообразной, но там не усложняется, остаётся точно так же как и было,  . Поэтому на следующем шаге интеграл содержит вообще не два множителя, а один!
. Поэтому на следующем шаге интеграл содержит вообще не два множителя, а один!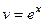
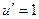
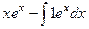 , тогда получаем ответ:
, тогда получаем ответ: 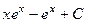 .
. .
.

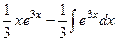 =
= 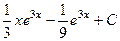 .
.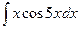 .
.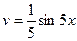
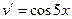
 =
= 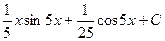 .
.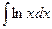 .
.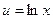

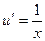
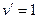
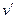 к
к 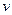 .
.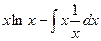 =
=  =
= 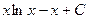 .
.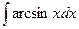
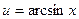 , второго множителя нет, но мы формально можем считать, что он есть, только равен 1. Итак,
, второго множителя нет, но мы формально можем считать, что он есть, только равен 1. Итак, 
 =
=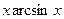
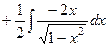 =
=  =
= =
=  .
. 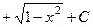 .
.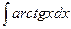
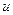 при интегрировании по частям:
при интегрировании по частям: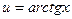
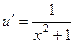
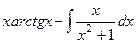 .
. =
= =
= 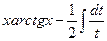 =
=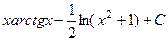 . Знак модуля даже не нужен, т.к.
. Знак модуля даже не нужен, т.к. 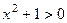 . Ответ.
. Ответ.  и
и  называются циклическими, потому что через 2 цикла вычисления «по частям» получается исходный интеграл в правой части выражения, т.е.
называются циклическими, потому что через 2 цикла вычисления «по частям» получается исходный интеграл в правой части выражения, т.е.  , откуда можно просто выразить
, откуда можно просто выразить 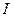 .
. .
.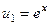 ,
,  .
.
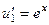
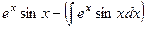 .
.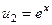 ,
, 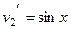 .
.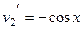
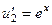
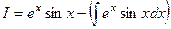 =
=  =
=  .
.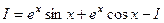 можно выразить
можно выразить  ,
,  .
.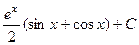 .
.
 .
.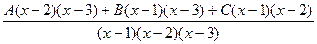 =
=  .
. .
. .
. чтобы её решить, построим расширенную матрицу системы и применим метод Гаусса.
чтобы её решить, построим расширенную матрицу системы и применим метод Гаусса.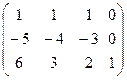
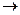
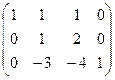
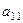 .
.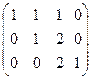 .
.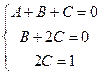 , т.е.
, т.е. 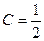 , тогда
, тогда  , а тогда
, а тогда 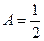 .
.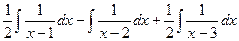 ,
,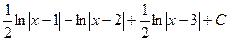 .
.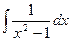 .
. .
.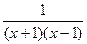 =
= 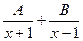 =
= 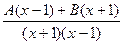 .
.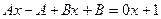 , тогда
, тогда , отсюда
, отсюда 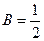 ,
, 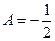 .
. =
=  =
=  .
. .
.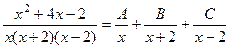 ,
, ,
, 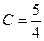 .
. 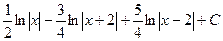 .
.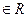 , но среди них есть кратные.
, но среди них есть кратные.
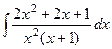 .
. означает, что корень 0 кратности 2. Фактически даже можем рассматривать в таком виде:
означает, что корень 0 кратности 2. Фактически даже можем рассматривать в таком виде: 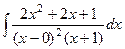 .
.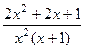 =
= 

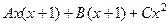 =
=  ,
, =
= 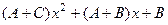 =
= 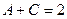 ,
, 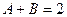 ,
, 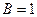 .
.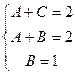 решая эту систему, находим
решая эту систему, находим 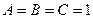 .
.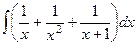 =
= 
 .
. .
. 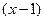 ,
, 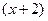 , т.е.
, т.е. 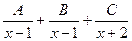 , иначе получится противоречие, ведь общий знаменатель будет содержать всего лишь 1-ю степень
, иначе получится противоречие, ведь общий знаменатель будет содержать всего лишь 1-ю степень 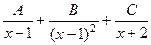 .
. .
. .
.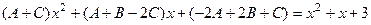 , система:
, система: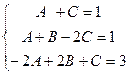 . Построим расширенную матрицу и решим систему уравнений:
. Построим расширенную матрицу и решим систему уравнений:
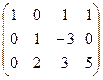
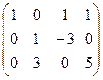 .
.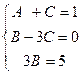
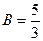 ,
,  ,
, 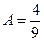 . И теперь интеграл распадается на сумму трёх интегралов:
. И теперь интеграл распадается на сумму трёх интегралов: 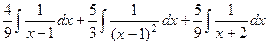 .
. .
. .
. .
. =
=  .
. =
= 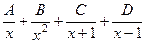 .
.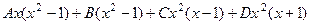 .
.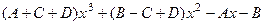 , это надо приравнять к
, это надо приравнять к . Получится систему с 4 неизвестными:
. Получится систему с 4 неизвестными: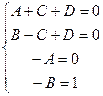 Поскольку A,B определяются сразу же,
Поскольку A,B определяются сразу же,  ,
, 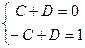 тогда
тогда 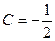 ,
,  .
.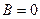 , иначе возникло бы противоречие при приведении к общему знаменателю.
, иначе возникло бы противоречие при приведении к общему знаменателю. =
=  .
. или
или 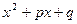 с отрицательным дискриминантом
с отрицательным дискриминантом 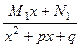 +
+ 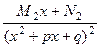 +...
+... .
.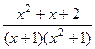 =
=  . Приводим к общему знаменателю.
. Приводим к общему знаменателю.
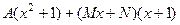 =
= 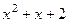
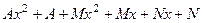 =
= 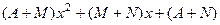 =
= 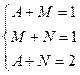 . Из разности 1-го и 2-го уравнения, получаем
. Из разности 1-го и 2-го уравнения, получаем 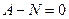 .
.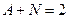 . Тогда
. Тогда  . Тогда
. Тогда  .
. =
=  .
.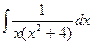 .
. 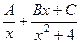 .
. .
.  .
.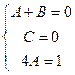 , итого
, итого 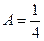 ,
, 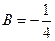 ,
, 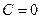 .
. .
.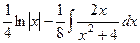 =
= 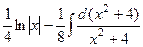 =
=  .
.


