
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Рекомендуемые домашние задачи.
Д-1 Д-2 Д-3 Д-4 Д-5. Д-6 Интегрирование рациональных дробей. Метод неопределённых коэффициентов. Случай 1. Если все корни Задача 308. Решение. Приведём к общему знаменателю Теперь приравняем числители в
Получается, что
Задача 309. Вычислить интеграл Решение. Разложение на простейшие дроби:
Приведём к общему знаменателю: Приравняем к исходной дроби. Знаменатели у них и так равны, осталось приравнять числители: из этого следует: Так как в исходном числителе была только константа 1, то искусственно приписали Получается система уравнений: Решаем систему, складывая уравнения между собой, получится
Ответ. Задача 310. Вычислить интеграл Решение.
Итак,
Ответ.
Задача 311. Вычислить Решение. В данном примере D>0, в отличие от предыдущих. Нужно сначала разбить дробь на сумму простейших:
и после этого, будет сумма двух таких интегралов, каждый из которых сводится к логарифму. Чтобы найти А и В, приведём к общему знаменателю:
Теперь приравняем числители, ведь дроби равны, знаменатели одинаковы, значит и числители тоже:
Отсюда получается система уравнений, из которой можно найти неопределённые коэффициенты А и В:
Решая эту систему, получаем
Ответ. Практика 28 (530 гр). Задача 312. Вычислить интеграл Решение. В данном случае знаменатель уже разложен в произведение множителей первой степени. Теперь представим дробь в виде суммы:
После приведения к общему знаменателю:
Тогда Перегруппируем слагаемые, так, чтобы вынести отдельно вторые степени, первые степени и константы.
Отсюда строим систему уравнений:
Сначала ко 2-й строке прибавили 1-ю, умноженную на 5, затем от 3-й отняли 1-ю, умноженную на 6. Так мы обнулили всё ниже углового элемента А теперь к 3-й строке прибавили 2-ю, умноженную на 3:
Уже получилась треугольная основная матрица. Ей соответствует такая система:
Теперь интеграл сводится к такому виду:
Ответ. Задача 313. Вычислить интеграл Решение. Сначала разложим знаменатель на множители:
Ответ. Задача (домашняя). Вычислить интеграл Кратко:
Ответ.
Случай 2. Если все корни
Задача 314. Вычислить интеграл Решение. Наличие множителя Сначала извлечём дробь из интеграла, и ищем разложение в виде:
Приводим к общему знаменателю.
Так как знаменатели равны, то осталось приравнять числители.
Тогда надо приравнять коэффициенты при каждой степени, получится То есть система уравнений на поиск трёх неопределённых коэффициентов:
Тогда исходный интеграл распадается на сумму:
= Задача 315. Вычислить интеграл Решение. Как видим, здесь корень 1 имеет кратность 2. Разложение на простейшие дроби нельзя проводить так, как будто бы здесь три независимых множителя Приведём к общему знаменателю:
Числитель этой дроби равен числителю исходной, той, которая была в интеграле:
Система приведена к виду: Тогда В 1 и 3 слагаемых - как раньше, а вот во 2-м логарифм в ответе не получится, ведь тут уже 2-я а не 1-я степень в знаменателе. Полезно вспомнить, что То есть, интеграл от -2 степени будет содержать -1 степень, и меняется знак.
Ответ.
Задача 316. Вычислить интеграл Решение. Здесь корень 0 имеет кратность 2, остальные корни простые.
После приведения к общему знаменателю, числитель будет такой:
После приведения подобных:
то матрицу 4 порядка для метода Гаусса строить не надо, а останется только маленькая система на C,D.
Ответ.
Случай 3. Если есть комплексные корни (не все корни Множители 2 степени типа Задача 317. Вычислить интеграл Решение. Ищем разложение в виде:
Получаем систему:
В то же время, Итак, заменим в интеграле «большую» дробь на сумму маленьких, каждая из которых приводится к табличному интегралу.
Итак, мы рассмотрели все типы рациональных дробей. Других случаев нет, т.к. неделимых множителей 3-й степени уже быть не может, для многочлена 3 степени есть хотя бы один действительный корень. Задача 318. Вычислить интеграл Решение. Запишем разложение на простейшие дроби: Это равно Тогда
Тогда Во втором слагаемом, можно подвести под знак дифференциала:
Ответ. «ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ»
|
||||||
|
Последнее изменение этой страницы: 2021-01-08; просмотров: 78; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.6.77 (0.06 с.) |
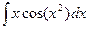 . Ответ.
. Ответ.  .
. . Ответ.
. Ответ.  .
.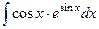 . Ответ.
. Ответ. 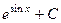 .
.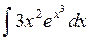 . Ответ.
. Ответ. 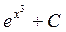 .
. . Ответ.
. Ответ. 
 . Ответ.
. Ответ. 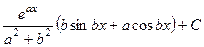 .
.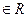 и различны
и различны 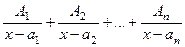
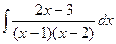 .
.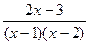 =
=  .
. .
.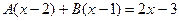 , т.е.
, т.е.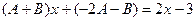 , получается система уравнений:
, получается система уравнений: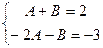 решая её, находим
решая её, находим 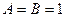 .
.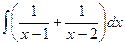 =
=  =
=  .
. .
.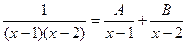 .
.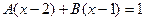
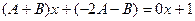 .
. , для того, чтобы присутствовали все степени, коэффициенты при которых надо сравнить.
, для того, чтобы присутствовали все степени, коэффициенты при которых надо сравнить.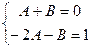
 , т.е.
, т.е. 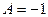 , тогда
, тогда 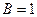 . Теперь интеграл можно разбить на два интеграла от таких слагаемых:
. Теперь интеграл можно разбить на два интеграла от таких слагаемых: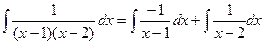 .
.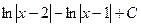 , либо в такой форме:
, либо в такой форме:  .
. .
. =
= 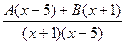 .
.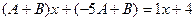 , тогда система уравнений для неопределённых коэффициентов:
, тогда система уравнений для неопределённых коэффициентов: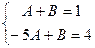 . Вычитая из 1-го уравнения 2-е, получим:
. Вычитая из 1-го уравнения 2-е, получим: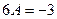 , т.е.
, т.е. 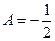 , тогда
, тогда 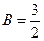 .
. =
= .
.  .
.
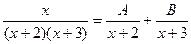 =
= 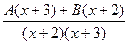 .
.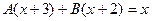

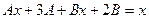
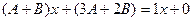 .
.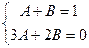
 ,
,  . Тогда интеграл распадается на простейшие:
. Тогда интеграл распадается на простейшие: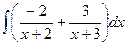 =
=  .
.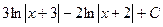 .
.
 .
.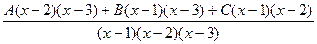 =
=  .
. .
. .
. чтобы её решить, построим расширенную матрицу системы и применим метод Гаусса.
чтобы её решить, построим расширенную матрицу системы и применим метод Гаусса.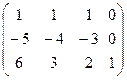
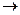
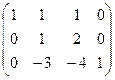
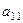 .
.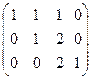 .
.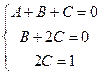 , т.е.
, т.е. 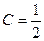 , тогда
, тогда  , а тогда
, а тогда 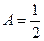 .
.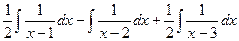 ,
,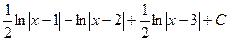 .
.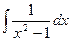 .
. .
.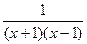 =
= 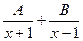 =
= 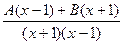 .
.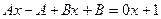 , тогда
, тогда , отсюда
, отсюда 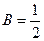 ,
,  =
=  =
=  .
. .
.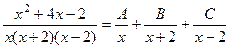 ,
, ,
, 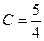 .
. 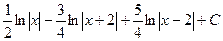 .
.
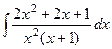 .
. означает, что корень 0 кратности 2. Фактически даже можем рассматривать в таком виде:
означает, что корень 0 кратности 2. Фактически даже можем рассматривать в таком виде: 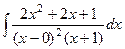 .
.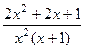 =
= 

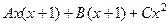 =
=  ,
, =
= 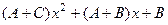 =
= 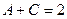 ,
, 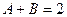 ,
, 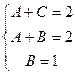 решая эту систему, находим
решая эту систему, находим 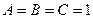 .
.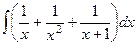 =
= 
 .
. .
. 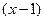 ,
, 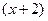 , т.е.
, т.е. 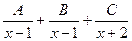 , иначе получится противоречие, ведь общий знаменатель будет содержать всего лишь 1-ю степень
, иначе получится противоречие, ведь общий знаменатель будет содержать всего лишь 1-ю степень 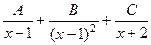 .
. .
. .
.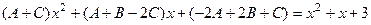 , система:
, система: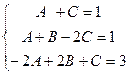 . Построим расширенную матрицу и решим систему уравнений:
. Построим расширенную матрицу и решим систему уравнений:
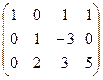
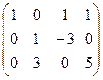 .
.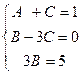
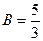 ,
,  ,
, 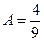 . И теперь интеграл распадается на сумму трёх интегралов:
. И теперь интеграл распадается на сумму трёх интегралов: 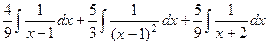 .
. .
. .
. .
. =
=  .
. =
= 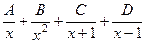 .
.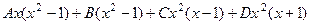 .
.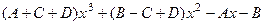 , это надо приравнять к
, это надо приравнять к . Получится систему с 4 неизвестными:
. Получится систему с 4 неизвестными: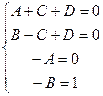 Поскольку A,B определяются сразу же,
Поскольку A,B определяются сразу же,  ,
, 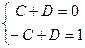 тогда
тогда 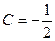 ,
,  .
.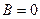 , иначе возникло бы противоречие при приведении к общему знаменателю.
, иначе возникло бы противоречие при приведении к общему знаменателю. =
=  .
. или
или 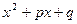 с отрицательным дискриминантом
с отрицательным дискриминантом 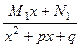 +
+ 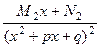 +...
+... .
.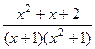 =
=  . Приводим к общему знаменателю.
. Приводим к общему знаменателю.
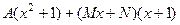 =
= 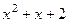
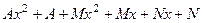 =
= 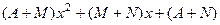 =
= 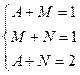 . Из разности 1-го и 2-го уравнения, получаем
. Из разности 1-го и 2-го уравнения, получаем 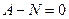 .
.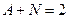 . Тогда
. Тогда  . Тогда
. Тогда  .
. =
=  .
.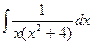 .
. 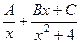 .
. .
.  .
.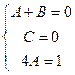 , итого
, итого 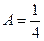 ,
, 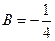 ,
, 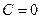 .
. .
.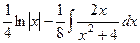 =
= 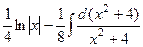 =
=  .
.


