
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Длина одной минуты дуги меридиана.
Длина S одной минуты дуги меридиана может быть определена из следующего равенства:
d S = M d j = следовательно, дуга меридиана между параллелями j1 и j2 будет: S = a (1-e2) Этот интеграл не выражается в элементарных функциях, поэтому подынтегральное выражение
Продолжим разложение значений Sin j. Sin2 j = ½ - 1/2Cos2 j - ………….. Sin4 j = 3/8 – 1/2Cos2 j + 1/8 Cos4 j + ………….тогда:
А = 1 + 3/4е2 + 45/64е4 + 175/256е6 + ………….. В = 3/4е2 + 15/16е4 + 525/512е6 + ……….Подставляя эти значения коэффициентов в знаменатель формулы (1.11) и, принимая dj = arc1¢, получим следующее выражение длины одной минуты дуги меридиана: S = a(1-e2) A arc1 ¢ - a(1-e2) B arc1 ¢ Cos2 j.
Подставляя значения параметров эллипсоида Красовского а и е2: а(1-е2) А = 6 368 027,5 а(1-е2) В = 32 073 и значение d j = arc1¢ = получим окончательно: S = 1852,25 – 9,31 Cos2j метры (1.12) Как видим, длина одной минуты дуги меридиана величина переменная, зависит от удвоенной широты места исследуемой точки и меняется в пределах от 1843,0 м на экваторе и до 1861,6 м на полюсе. В навигации принято Землю принимать за шар, у которого длина одной минуты дуги меридиана равна округленной до целого значения величины 1852 метра. Эту величину морской мили в метрах узаконили на Международном гидрографическом бюро в Монако в 1928 году.
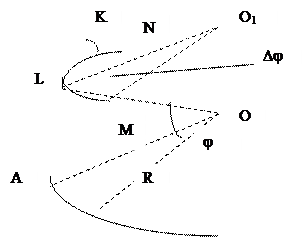
Длина одной минуты дуги параллели Исходя из условия кривизны любой кривой, можно записать выражение для длины 1 минуты дуги параллели: Р = r arc1¢ Ранее мы нашли, что х = r, тогда вместо r подставим значение координаты х и запишем: Р = r arc1¢ = Эксцентриситет Ортодромия локсодромия Используя навигационные морские карты, судоводители прокладывают на них путь в виде прямой линии. Из условия построения карты, такой прямой путь на карте не будет кратчайшим на местности. Путь (прямая), проложенный на карте в Меркаторской проекции называется локсодромией (кривой бег). Кратчайший же путь между двумя точками на земной поверхности эллипсоида является сложной кривой, называемой геодезической линией. На поверхности сферы (шара) кратчайшее расстояние между двумя точками измеряется по дуге большого круга, т.е. круга, образованного пересечением плоскости, проходящей через центр сферы и заданные точки, со сферической поверхностью. Такая дуга в навигации называется ортодромией (Рис.1.6). Уравнение ортодромии, проходящей через заданные точки, имеет вид:
CtgA1 = tgj2 Cosj1CosecDl - Sinj1 CtgDl (11), где: А1 – направление ортодромии в точке В1, Dl - разность долгот точек В2 и В1.
1. при расположении точек В1 и В2 на одном меридиане ортодромия совпадает с меридианом этих точек. 2. ортодромия пересекает меридианы под разными углами (А0, А1, А2), 3. при расположении точек по экватору ортодромия совпадает с экватором.
Р азность углов, под которыми ортодромия пересекает меридианы двух точек, называется сближением (схождением) меридианов. γ = А2 – А1. Угол схождения меридианов рассчитывается по приближенной формуле:
γ = 2arc tg [tg( Основные свойства локсодромии:
ному на косинус широты этой параллели. Возьмем на локсодромии две точки М1(j1, l1) и М2(j2, l2) (Рис. 1.8a), находящиеся на малом расстоянии одна от другой (dS). Из элементарного треугольника М1 М2 С (Рис.18.b) имеем: tgK =

получим уравнение локсодромии: l2 - l1 = tg K [ln tg(p/4+j2/2) – ln tg (p/4 + j1/2)] (1.15) Возвращаясь к форме Земли как сфероиду, локсодромия примет вид: l2 - l1 = tg K локсодромия на навигационной карте: y – y0 = (x – x0) tgK, (l - l0)¢ = (D – D0)¢ tg K, РД = РМЧ tg K (1.16)
l0 l
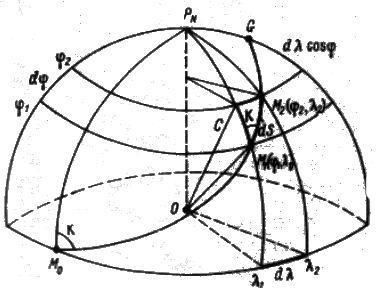
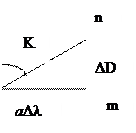
Меридиональные части Для упрощения решения задачи примем форму Земли в виде шара. Рассмотрим элементарный треугольник на поверхности шара D LMN и его проекцию на плоскость D lmn (Рис.1.10 и 1.11). При проектировании треугольника с поверхности шара на плоскость, меридианы изобразятся параллельными прямыми, перпендикулярными линии экватора, а параллели прямыми, параллельными экватору. По малости треугольника D LMN можно рассматривать его как плоский и прямоугольный. Тогда катет È MN = а Dj, а катет È LM = r Dl = а Dl Cosj. В треугольнике D LMN отношение катетов будет: В элементарном треугольнике lmn катеты будут по меридиану dx, а по параллели - dy, но dy = adl. Переходя к конечным приращениям, имеем dx =DD, dy=aDl.
Тогда в треугольнике D lmn на плоскости, отношение катетов запишется: Исходя из подобия треугольников и равенства углов, можно записать: откуда
Проинтегрировав выражение (1.17) в пределах от 0 до j, получим:
Величина D называется меридиональной частью и представляет собой расстояние по меридиану от экватора до заданной параллели в минутах дуги экватора. Выражая меридиональную часть через длину дуги экватора, примем: а = 3437,747 экв. миль. Далее для перехода от натуральных логарифмов к десятичным, введем модуль логарифмов: mod = 0,434294. Тогда: D = D = 7915,705 lgtg(45 + С учетом сжатия Земли выражение перепишется в следующем виде: D¢ = 7915,70447 lg tg (45 + По этой формуле составлены таблицы «Меридиональные части» в МТ любого года издания.
Пример 1: Во сколько раз меркаторская миля в широте j1 = 71 °30 больше меркаторской мили в широте j2 = 26 °30 ¢? Решение. Из мореходных таблиц выбираем значения меридиональных частей для приведенных в задаче широт j1 = 71°30 МЧ = 6217,2 j = 71°31 МЧ = 6220,4 j2 = 26°30¢ МЧ = 1639,7 j = 26°31 МЧ = 1640,8 Для j1 при РШ = 1¢ РМЧ1 = 3,2 Для j2 при РШ = 1¢ РМЧ2 = 1,1. Вычисляем отношение полученных РМЧ и тем самым находим ответ на поставленный вопрос задачи: Пример 2: Рассчитать длину одной минуты меридиана в широте Одессы j = 46 °35 ¢ N. Решение. Для расчета применим формулу: S = 1852,25 – 9,31 Cos2j. Подставив значение широты 46°35¢, получим длину одной минуты меридиана в метрах: S = 1852,2 – 9,31 Cos 93°10¢ = 1852,2 – 9,31 * 0,0552 = 1851,7 м.
Контрольные вопросы
Глава 3 Видимый горизонт
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-01-08; просмотров: 293; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.195.121 (0.045 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 (1.10),
(1.10),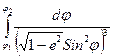 (1.11)
(1.11) разложим в ряд, получим:
разложим в ряд, получим: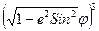 = 1 + 3/2 e2 Sin2 j + 15/8 e4 Sin4 j + 105/48 e6 Sin6 j + ……..
= 1 + 3/2 e2 Sin2 j + 15/8 e4 Sin4 j + 105/48 e6 Sin6 j + ……..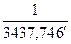
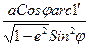 , вместо arc1 ¢ и а подставим их значения и получим окончательно:
, вместо arc1 ¢ и а подставим их значения и получим окончательно: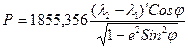 метр (1.13)
метр (1.13) , а е2 = 0,0066934
, а е2 = 0,0066934 При анализе уравнения ортодромии можно сделать следующие выводы:
При анализе уравнения ортодромии можно сделать следующие выводы: ) Sin jср] (1.14)
) Sin jср] (1.14)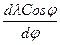 , откуда d l = tgK
, откуда d l = tgK  , проинтегрировав это последнее выражение, получим:
, проинтегрировав это последнее выражение, получим: , после решения интегралов,
, после решения интегралов, ln tg (
ln tg (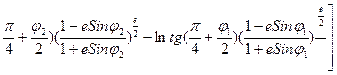

 D
D Рис.1.9
Рис.1.9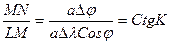






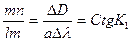
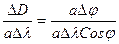 ,
,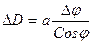 , переходя из конечных приращений к дифференциалам, получим:
, переходя из конечных приращений к дифференциалам, получим: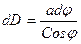 . (1.17)
. (1.17)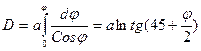 (1.18)
(1.18)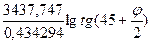 .
. ) (1.19)
) (1.19) (1.20)
(1.20)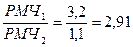 раза.
раза.


